两圆无交点，圆系为何意——记一次对虚圆系的探究过程

●

(湖州市第二中学 浙江湖州 313000)

两圆无交点，圆系为何意
——记一次对虚圆系的探究过程

●刘薇陆丽滨

(湖州市第二中学 浙江湖州 313000)

1 起源

在课堂上讲解两圆相交等知识时，笔者出示了人教A版数学必修2习题A组第10题：

求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点，并且圆心在直线上的圆方程．

这是一道典型的运用圆系思想、避免解交点的圆系问题．下面是笔者在课堂上讲解课本例题的部分过程：

教师：……同学们知道，只要令

x2+y2+6x-4+λ(x2+y2+6y-28)=0，

可得

(1+λ)x2+6x+(1+λ)y2+6λy-4-28λ=0，

(1)

x2+y2-x+7y-32=0.

……

学生：比起刚刚我自己求交点的算法，这种方法简单多了！

教师：因此，利用圆系理论求解涉及两曲线交点的问题，常常可以避开繁杂的运算，并使解题的思路变得流畅、清晰和自然．

2 疑问

正以为问题解决之际，有学生刚下课就问了笔者一个难以回答的问题！

学生：老师，如果两圆无交点，那么圆系还有没有用？

教师：两圆相交、相切均有用，相离没用．

学生：老师，这就奇怪了，我刚刚自己演算了一个问题，两圆是无交点的，但是圆系还是可以解出这样一个圆方程，这是为什么？

笔者仔细查看了学生演算的那道题目：两圆方程C1：x2+y2=1，C2:(x-4)2+y2=1，求经过两圆交点，并经过点(0,0)的圆方程．

学生解法：令所求圆方程为

x2+y2-8x+15+λ(x2+y2-1)=0,

(2)

代入点(0，0)，可得λ=15.代入式(2)，解得圆方程为

即

学生：可是，我画图时发现2个圆是没有交点的！而且我还解了方程组

解得x=2,y2=-3，无意义啊！那我刚刚计算出来的到底是什么呢？

听到此处，笔者大惊！这是笔者以前从来没有探究过的问题！为此，笔者和学生一起做了探究．

3 探究

笔者冥思苦想，一直毫无头绪．为何没有交点的圆系方程也能求之，难道就是增根这么简单？笔者还查询了诸多资料，也没有任何资料显示到底原因为何，只是叙述此种情况为不合而已！

正在悬疑之际，学生的一句话提醒了笔者,“老师，你看方程的解y2=-3，好像复数中的虚根！”是啊！我怎么就没有想到？虚根——不正好对应同顶点的双曲线的解吗？

于是，笔者与学生一起将原来的两圆方程C1:x2+y2=1，C2:(x-4)2+y2=1改写成2个双曲线方程C1′:x2-y2=1,C2′:(x-4)2-y2=1．联立双曲线方程

解得

x=2,y2=3.

x2-y2-8x+15+λ(x2-y2-1)=0,

(3)

代入点(0，0),可得λ=15.代入式(3)，解得双曲线为

即

如图1所示，经检验结论正确．

图1

最终，我们对比求出的圆系方程和双曲线方程，发现竟然也是如此的统一！因此，可以说尽管两圆无交点，但是与其相对应的双曲线却呈现出了这一切！因此，笔者总结得到以下定理：

4 再探

若两圆内含呢？请看继续探究：两圆方程C3:x2+y2=16，C4:(x-1)2+y2=1(内含)，求过两圆交点(虚)且过点(-1,0)的圆方程．

现将圆方程改成相对应的双曲线方程：

令过上述2个点的双曲线系方程为

x2-y2-2x+λ(x2-y2-16)=0，

(4)

图2

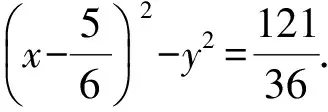
如图2所示，经检验结论正确．这说明当两圆内含时，定理1也成立．

5 释疑

当两圆相交、相切时圆系的方程是有意义的，现在通过探究发现，当两圆相离、内含时,尽管圆系方程并无实际意义，但以其对应的双曲线系方程必过(虚)交点而可得，又与所得(无实际意义)的圆系恰好相对应．

笔者将上述现象称为虚圆系．

6 尾声

在探究知识之后，尽管此现象并无实际意义，而且以上的探究过程也花费了很多时间(包括课内和课后),但从远期目标来看:这有助于学生了解问题解决的过程，初步尝试数学研究的过程，从而建立起严谨的科学态度和不怕困难的科学精神；有助于培养学生善于质疑的习惯，培养学生提出问题、解决问题的能力．另外，教师还应加强自身的专业素养，不断在教学工作中提升自己.只有不断钻研，才能用自己的“一桶水”浇灌给学生的“半桶水”．

通过学生的质疑，使得笔者和学生一起弄清了两圆无交点，圆系为何意,增长了学习数学的兴趣，引导学生对数学中感到困惑的问题进行探究.这不仅是“释疑、解惑”的需要，也是新课改倡导的培养学生探究意识和理性精神的需要．