数学解题中的规定动作与自选动作

● (北仑中学 浙江宁波 315800)

数学解题中的规定动作与自选动作

●吴文尧(北仑中学 浙江宁波 315800)

马克思说过“数学是思维的体操”.众所周知，现在的体操比赛分规定动作的比赛与自选动作的比赛，作为思维体操的数学，其实也有规定动作与自选动作之分.在高考数学试卷中规定动作所占的比例要大一些，而自选动作所占的比例相对要小一点，且有时很难做到严格分类.在高考复习中，如何面对规定动作与自选动作的问题呢？本文以有关三次函数的问题为例，讨论应对策略，供大家参考．

1 规定动作问题——熟悉解题程序，操作正确规范

三次函数问题一直是近几年高考数学中的一个热点问题，通常涉及三次函数的解析式的确定、单调性问题、函数图像的切线方程、函数的零点个数问题、函数中的参数范围问题、三次函数的综合应用问题等．其中除最后2个问题以外，都应属于规定动作的范畴．对于规定动作问题，通常可用程序化的方法解决之.若能熟悉其解题一般程序，则只须按程序规范操作，即可得到所需的结论．例如有关一元三次方程实根的分布情况问题(即三次函数的零点个数问题)的解题程序可总结如下：

图1

(2009年江西省数学高考文科试题改编)

解由f′(x)=3x2-9x+6=3(x-1)(x-2)=0,得

x1=1,x2=2.

f(x)=0有且仅有1个实根等价于f(x1)f(x2)>0,即f(1)f(2)>0,因此

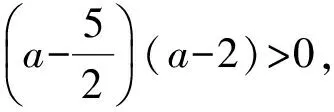
解得

例2已知函数f(x)=x3-3x-m-1的图像与x轴有3个不同的交点，求m的取值范围．

(2009年陕西省数学高考文科试题改编)

解由f′(x)=3x2-3=3(x+1)(x-1)=0,得

x1=-1,x2=1.

f(x)=0有且仅有3个实根等价于f(x1)f(x2)<0,即f(-1)f(1)<0,因此

(m+3)(m-1)<0,

解得

-3

2 自选动作问题——明确问题关键,数学思想引路

对于高考试题,“难题”之所以是“难题”，往往有以下2种原因:其一是问题的情景比较陌生，但问题的本质比较常规,其实是经过命题者过度“包装”的“伪难题”，对于这类问题若能剥去其过度的“包装”，看到问题的本质，还是数学中的规定动作，因此不难得到解决；其二是对数学能力要求较高的真难题，即所谓数学中的自选动作，解决这类问题虽然没规定的套路，但解决问题的总的指导思想是不会改变的，若能注意运用函数与方程、数形结合、分类讨论、等价转化等数学思想方法去分析和解决问题，则往往能找到解决问题的通途．

例3已知函数f(x)=(1-2a)x3+(9a-4)x2+(5-12a)x+4a(a∈R)在区间[0,2]上的最大值是2，求a的取值范围．

(2009年浙江省数学调研试题改编)

分析(1)当a的值确定时,f(x)在区间[0,2]上的最大值也随之确定.从理论上讲,其最大值可以表示成关于a的函数h(a),解方程h(a)=2可得到a的值.但这个想法有以下2个方面的不足:①求函数h(a)的解析式是一件很不容易的事,没有可操作性;②照理可求出a的值,而问题所要的结论是求a的取值范围,因此题目中可能还隐藏着其他的“机关”.

(2)注意到函数f(x)在区间[0,2]上的最大值只可能在边界点的函数值及在这个区间上的极值点的函数值中产生,因此必有f(0)≤2,f(2)≤2成立,由此可缩小“包围圈”．在操作过程中未必要真的求出其最大值，只需在区间[0，2]上的极值点的函数值不大于2且可以取到2即可．

解法1(分类讨论,逐个击破)

因为f(x)=(1-2a)x3+(9a-4)x2+(5-12a)x+4a(a∈R)，所以

f′(x)=3(1-2a)x2+2(9a-4)x+(5-12a)=

(x-1)[3(1-2a)x-(5-12a)].

f(1)=-a+2≤2,

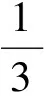
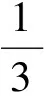
f(t)<2等价于

(5-12a)2(2-3a)<54(1-2a)3,

解得

9a<4.

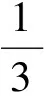
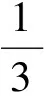
解法2(大胆猜想,小心论证)

f(1)=-a+2≤2,

分析发现“暗藏机关”:f(2)=2后，问题即化归为“当0≤x≤2时,f(x)≤f(2)恒成立，求实数a的取值范围”.运用分离变量法可把问题化归为求函数的最值，是求解不等式中参数范围最常用的方法之一，因此还可以运用分离变量法解决问题.

解法3(分离变量,再求最值)

(x-2)[(-a)(2x2-5x+2)+x2-2x+1]≤0

恒成立,亦即当0≤x<2时,

a(x-2)(2x-1)≤x2-2x+1

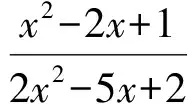
评注以函数的思想为指导，运用分离变量的方法求解参数的范围，显得思路自然，唯一要担心的是实施分离变量后所得目标函数的最值能否顺利求得；注意到x=2是关于x的方程f(x)=f(2)的解,因此可以预见关于x的三次不等式f(x)≤f(2)必可化简为关于x的二次不等式(可以消去因式x-2).因而上述担心是多余的，用分离变量法还是具有可操作性的.

武术的最高境界是——无招胜有招，即到达随心所欲境界.要达到这种境界必须要经过从“有招”再到“无招”的心路历程,数学解题也是如此.多数考生很难到达“无招胜有招”的境界，因此做好数学解题中的“规定动作”是高考数学取得高分的必要条件．例3确实已属高考题中的难题，对能力的要求较高，对于这类有关“自选动作”的问题，在平时复习备考中，还是要以不变应万变，在提高分析问题和解决问题的能力上下功夫.不管问题多么复杂，最后一般都可以化归为“规定动作”的问题，所以高考数学考的是数学的功底．