习题教学中如何培养学生的数学思维品质
● (春晖中学 浙江上虞 312353)
习题教学中如何培养学生的数学思维品质
●孟方明(春晖中学 浙江上虞 312353)
新课程标准明确指出:“高中数学课程应注重提高学生的数学思维能力,这是数学教育的基本目标之一”,“数学思维能力在形成理性思维中发挥着独特的作用”[1].2010年浙江省高考考试说明(理科)在数学能力考查方面也明确指出:“对数学能力的考查,应检测考生个体理性思维的广度和深度”.可以说,数学教学就是思维的教学,培养思维能力,从根本上就是如何提高学生的思维品质.
习题教学是数学教学的一个重要组成部分,习题教学对于深化基础知识、培养解题技巧、开发智能结构具有十分重要的作用,是培养学生数学思维品质的重要途径.如何在习题教学中培养数学的思维能力,养成良好的思维品质是教学改革的一个重要课题.笔者结合教学实践谈谈自己的一些做法与体会.
1 注重观察,培养思维的敏捷性
思维的敏捷性是指思维活动的反应速度和熟练程度,它反映了智力的敏锐程度.主要表现为能缩短运算环节和推理过程,正确和迅速地得出结论[2].实践表明,解题成功与数学观察密切相关,观察是思维的起点,是类比的基础,是联想的羽翼.在教学中引导学生注重数学观察,有利于培养学生思维的敏捷性.

(1)若f(x)在其定义域内为单调函数,求p的取值范围;
(2)若直线l与函数f(x),g(x)的图像都相切,且与函数f(x)的图像相切于点(1,0),求p的值;
(3)若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求p的取值范围.
(2009年浙江省绍兴市高三期末调测试题)
分析(1),(2)略.
(3)含参存在性(或恒成立)问题的解法一般有2种:第1种是分离变量法,将参数的取值范围转化为新函数的最值;第2种是移项构造含参的新函数,通过分类讨论求含参函数的最值.通常首选分离变量法.由f(x)>g(x),得
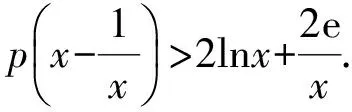
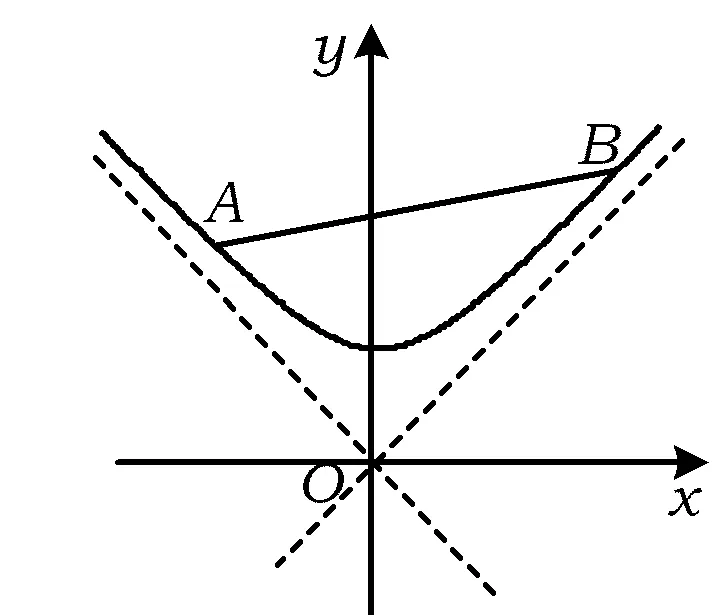
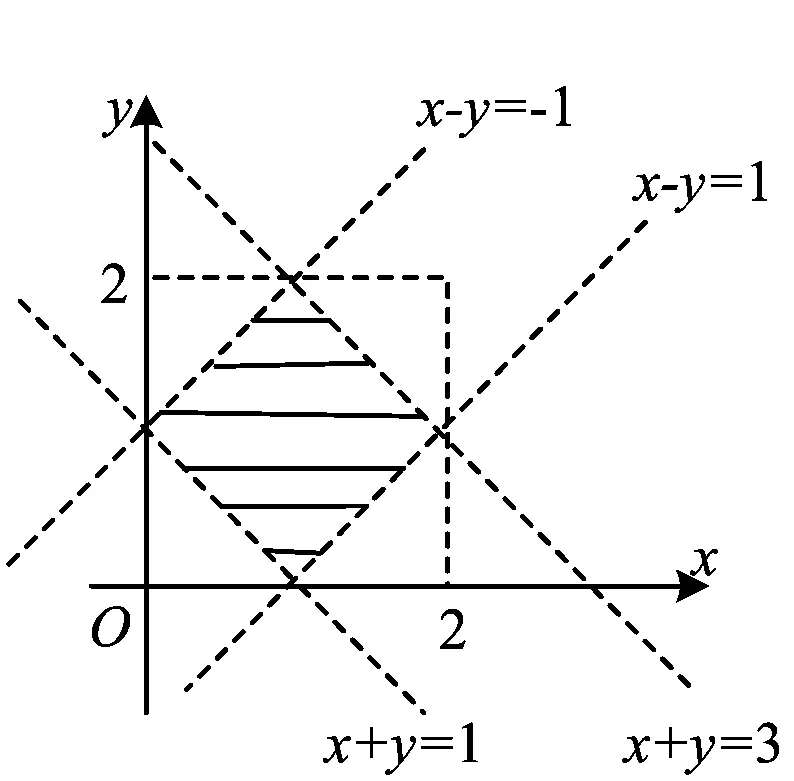
若x=1,则p无解;若1 到此,学生的第一感觉往往是难以直接解出F′(x)>0或F′(x)<0的解集(因为分子是既含对数函数,又含幂函数的超越式),从而毫不犹豫地进行第2次求导.设 g(x)=x2-x2lnx-lnx-2ex-1, 则 此时,有些学生已经觉察到由x-2e<0,可得g′(x)<0,从而g(x)递减,于是 g(x) 则F′(x)<0,即F(x)递减,从而 故 但有些学生认为g′(x)的形式仍然无法求解,继续求导.其实,一阶导数中对g(x)的各项重新搭配,可得 g(x)=x(x-2e)-x2lnx-lnx-1. 这显然是负值,因此完全可以避免2次甚至3次求导.因而教师在教学时应引导学生在一次求导得到超越式后,不急于2次求导,而是注重观察,看是否可以通过诸如提取公因式等方法进行化简,或者是通过项的重新搭配直接得出函数的取值为恒正(或恒负).若上述观察不奏效,再进行2次求导. 点评数学观察极大地简化了解题过程,有效地提高了解题的效率.当然,数学观察不局限于观察式子的特殊性,还可观察题设的对称性、题断的隐蔽性等等. 思维的广阔性是指思维活动作用范围的广泛和全面的程度.它表现为解题思路开阔,能全面地分析问题,多方向、多角度地思考问题[2].一题多解能有效地帮助学生夯实“双基”,是培养学生思维广阔性的一种有效途径. |f(a)-f(b)|<|a-b|. 分析本题的突破口较多,可从去绝对值、有理化、图像特征等角度加以思考. 证明1不等式两边都是绝对值,可考虑通过平方去绝对值符号,实现问题简化. 原不等式等价于 即 a2+b2-2ab, 化简得 (1) 若1+ab≤0,则式(1)显然成立;若1+ab>0,则式(1)等价于 (1+ab)2<(1+a2)(1+b2), 即 (a-b)2>0, 故原不等式成立. 图1 从而 |f(a)-f(b)|<|a-b|. 易见AB连线的斜率介于2条渐近线之间,从而 |kAB|<1. 点评教师引导学生从不同的角度进行分析探究.这不但使相关的知识得到了梳理和巩固,同时也培养了学生举一反三、触类旁通的思维能力. 思维的灵活性即思维活动的灵活程度,是指能够根据客观条件的发展与变化,及时地改变先前思维过程或方式,寻求新的思维角度和方向.它表现为思考问题和解决问题时所用方法的新颖、独特等特征[2].在习题教学中,当学生遭遇挫折后,教师应及时引导学生对问题的解法进行反思总结,另辟蹊径,突破常规,激发学生的创造力,培养其思维的灵活性. (1)当x=1时,f(x)取到极值,求a的值; (2)设不等式f′(x)>x2-x-a+1对任意a∈(0,+∞)都成立,求实数x的取值范围. (2008年安徽省数学高考试题) 分析(1)略. (2)原不等式等价于 ax2-3x+a+1>x2-x-a+1. 点评一个问题常含有好几个量,“常量”、“参量”、“变量”的定位往往不是绝对的.定位不同,解题途径也就不同.打破常规,正确定位,使解题过程显得干净、利落,充满数学美感. 思维的批判性是指思维活动中善于严格地估计思维材料和精细地检查思维过程的智力品质,反映了思维活动过程中独立分析和批判的程度.它表现为善于思考,敢于质疑,并能及时发现和纠正错误,自觉调控思维过程,对问题及问题的自我解法进行评价[2].实践表明,在习题教学中,教师创设质疑氛围,鼓励学生自主探究、发现,有利于培养学生理性的思维习惯. 例4已知 求4x+2y的取值范围. 解式(2)+式(3),得 0≤2x≤4, 即 0≤4x≤8. (4) 式(3)×(-1),得 式(2)+式(5),得 式(4)+式(6),得 0≤4x+2y≤12. 教师给出上述解答后,请学生观察、判断、讨论,这个解法是否正确?许多学生只从表面研究上述解法的过程,认为应用不等式性质处理无懈可击,怎么会出错呢?不过,马上有学生发现:当x取到最大值2时,代入式(2),得-1≤y≤1,与式(6)矛盾,从而0≤4x+2y≤12中的12取不到,即范围被放大了. 教师追问能否从错解中获得启示,得到问题的正确解法.教师引导学生自主讨论,产生了不少正确的解法. 正解1设x+y=m,x-y=n,得 1≤m≤3,-1≤n≤1, 则 于是 4x+2y=3m+2n, 从而 2≤4x+2y≤10. 图2 正解2用线性规划的知识加以处理,原不等式表示的平面区域为如图2所示的阴影部分.作出目标函数t=4x+2y,易知过点(0,1)时,tmin=2;过点(2,1)时,tmax=10,从而2≤4x+2y≤10.此时也进一步明晰了错解中得到的0≤x≤2,0≤y≤2表示的平面区域是包含阴影的正方形,范围被扩大了[3]. 点评教师有意地设置错解,让学生辨别真伪,寻找错误根源,质疑思辨,并以此探索问题的正解,使思维的批判性得到了一次有效的训练. 思维的深刻性指思维活动的抽象程度和逻辑水平,反映了思维活动的广度和深度.它表现为能洞察对象本质以及揭示对象间的相互关系,能够抓住问题的本质和规律,对问题进行深入细致地分析和推广[2].在习题教学中,通过改编命题、一题多变能让学生加深对题目的理解和把握,培养学生思维的深刻性. 教师将问题变换成一个探究性、开放性命题: 解假设存在点P,则 (a+ex)2+(a-ex)2=4c2, 得 2e2x2=4c2-2a2≥0, 在这里,教师改编命题,创设新境,引导学生自主探究,极大地激发了学生的学习热情.教师趁热打铁,引导学生抓住|PF1|,|PF2|,|F1F2|之间的关系进行拓广.思考如下变题: 点评在习题教学中,教师不拘泥于就题论题,而是适时对典型例题进行有效的改造变换、挖掘延伸,从而使问题层层深入,思维不断深化. 数学是思维的体操,习题教学是培养思维品质的良好场所.在平时的习题教学中,教师应侧重揭示方法的探索和选择,暴露其思维过程,经历体验感悟.习题的选择要在运用知识的广度、思维训练的强度、发展智能的效度等方面作全面考虑,充分发挥习题的价值,不断提升学生的思维能力和思维品质. [1] 中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003. [2] 任樟辉.数学思维论[M].南宁:广西教育出版社,1996. [3] 徐润权.质疑思辨 培养理性思维[J].数学教学研究,2009(5):22-23. [4] 马灿宏.培养学生的创新思维[J].中学数学,2005(1):8-9.
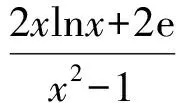
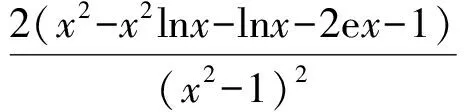
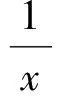


2 一题多解,培养思维的广阔性
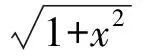
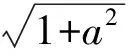
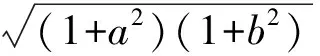
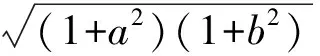
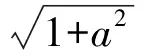
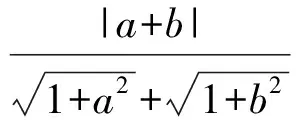
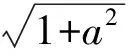
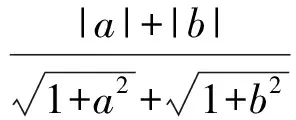
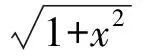
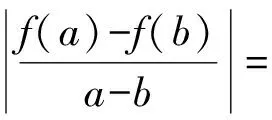
3 突破常规,培养思维的灵活性
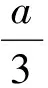
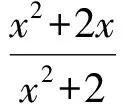
4 质疑思辨,培养思维的批判性

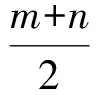
5 变换命题,培养思维的深刻性