中考试题中的动态型问题解析
● (武威市第十三中学 甘肃武威 733000)
中考试题中的动态型问题解析
●满银天(武威市第十三中学 甘肃武威 733000)
在近几年各地的中考试卷中,动态型问题已成为中考试题的一大热点题型,而且常常作为压轴题出现.这类问题以几何图形为载体,以运动变化为特征,通过图形在运动中产生的函数关系问题和探究几何图形变化规律的问题,考查学生对图形的直觉能力以及从变化中看到不变实质的数学洞察力.在运动变化中发展学生的空间想象能力,综合提高分析能力.解决动态几何题的策略是:把握运动规律,寻求运动中的特殊位置;“动”中求“静”,在“静”中探求“动”的一般规律.通过探索、归纳、猜想,获得在运动过程中不变量与变量之间的特殊关系,从而建立函数模型或方程模型,找到解题的突破口.下面以2009年各地中考试题为例,将动态型问题进行分类解析.
1 动点型
例1如图1,在正方形ABCD中,点A,B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当点P到达点D时,两点同时停止运动,设运动的时间为t秒.
(1)当点P在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图像如图2所示,请写出点Q开始运动时的坐标及点P的运动速度.
(2)求正方形边长及顶点C的坐标.
(3)在第(1)小题中,当t为何值时,△OPQ的面积最大,并求此时点P的坐标.
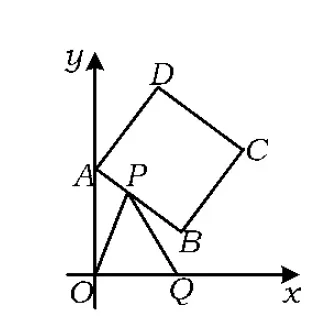
图1
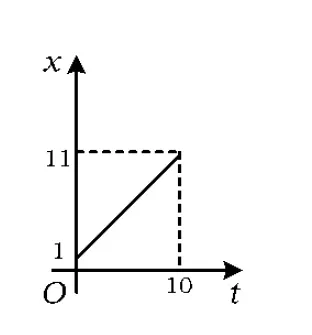
图2
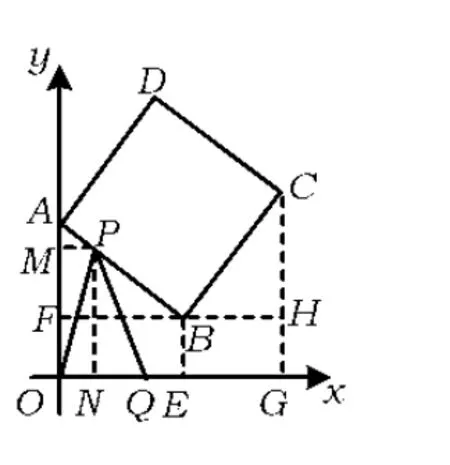
图3
(4)如果点P,Q保持原速度不变,那么当点P沿A→B→C→D匀速运动时,OP与PQ能否相等.若能,写出所有符合条件的t的值;若不能,请说明理由.
解(1)Q(1,0),点P的运动速度为每秒1个单位长度.
(2)过点B作BF⊥y轴于点F,BE⊥x轴于点E,则
BF=8,OF=BE=4.
求得点C的坐标为(14,12).
(3)过点P作PM⊥y轴于点M,PN⊥x轴于点N,则△APM∽△ABF,可得

于是

设△OPQ的面积为S(平方单位),则
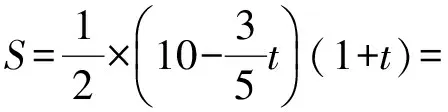
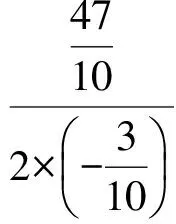
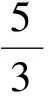
评析本题将点的运动过程中形成的函数解析式与其相应的函数图像有机地结合起来,并把这些点在运动变化过程中产生的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等联系起来进行研究,融入了数形结合、分类讨论、函数等数学思想.求解本题的关键是确定△OPQ的底长OQ、高PN与t的关系式,从而建立起面积与t的函数关系,以静制动,运用所学函数知识求出△OPQ的面积最大时t的值.
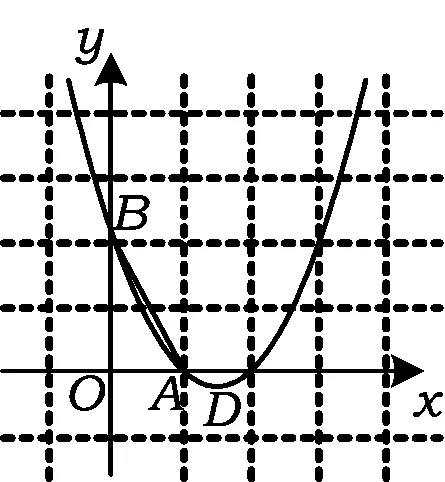
图4
2 三角形的运动
例2如图4,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.
(1)求抛物线的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图像的函数关系式;
(3)设第(2)小题中平移后所得抛物线与y轴的交点为B1,顶点为D1,若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标.
解(1)已知抛物线y=x2+bx+c经过点A(1,0),B(0,2),解得b=-3,c=2,于是所求抛物线的解析式为y=x2-3x+2.
(2)因为A(1,0),B(0,2),所以
OA=1,OB=2.
可得旋转后点C的坐标为(3,1),于是平移后的抛物线解析式为y=x2-3x+1.
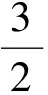
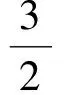
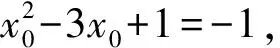
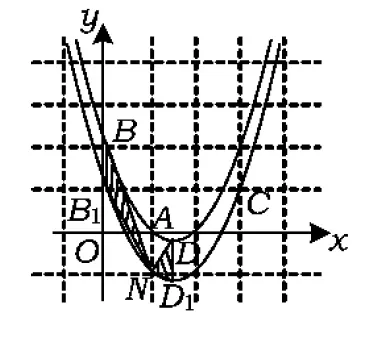
图5
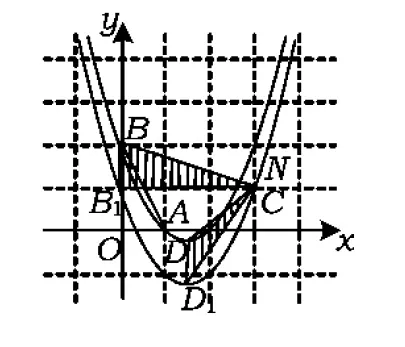
图6
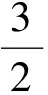
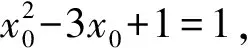
综上所述,点N的坐标为(1,-1)或(3,1).
评析本题是以三角形旋转运动为载体、以抛物线为背景创设的探索性问题.试题由浅入深、层层递进,涉及了三角形和二次函数等知识的考查.解决此题的关键是应弄清图形运动过程中始终保持不变的量.这里融入了动态几何中的变和不变、数形结合、分类讨论的思想.
3 矩形的运动
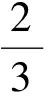
(1)求△ABC的面积;
(2)求矩形DEFG的边DE与EF的长;
(3)若矩形DEFG从原点出发,沿x轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤12)秒,矩形DEFG与△ABC重叠部分的面积为S,求S关于t的函数关系式,并写出相应的t的取值范围.
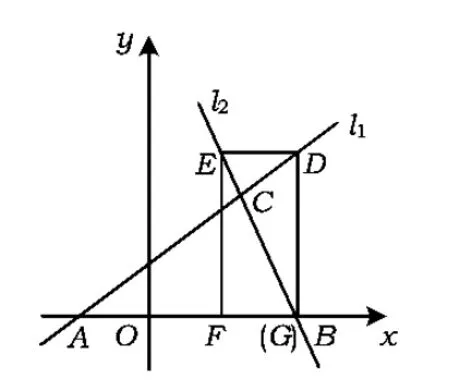
图7
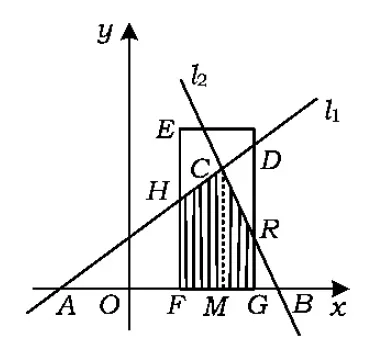
图8
解(1)易得直线l1,l2的交点C的坐标为(5,6),因此

(2)由点D在l1上,得点D的坐标为(8,8).又由点E在l2上,可得点E的坐标为(4,8),于是
OE=8-4=4,EF=8.
(3)当0≤t<3时,如图8,矩形DEFG与△ABC重叠部分为五边形CHFGR(当t=0时,为四边形CHFG).过点C作CM⊥AB于点M,则
Rt△RGB∽Rt△CMB,
于是
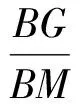
即
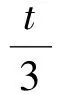
解得
RG=2t.
由Rt△AFH∽Rt△AMC,可得
S=S△ABC-S△BRG-S△AFH=

即
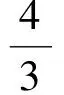
②当3≤t<8时,如图9,矩形DEFG与△ABC重叠部分为梯形HFGR.过点C作CM⊥AB于点M,则
Rt△ARG∽Rt△ACM,
因此
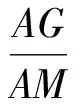
即
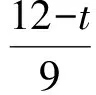
解得
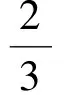
又由Rt△AHF∽Rt△ACM,可得
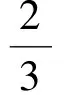
于是

解得

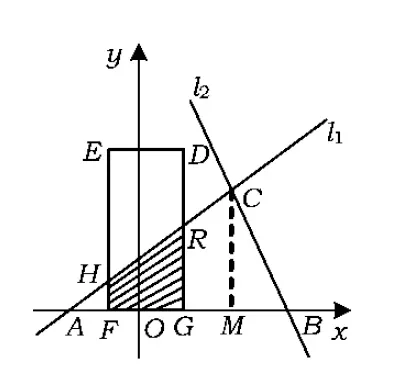
图9
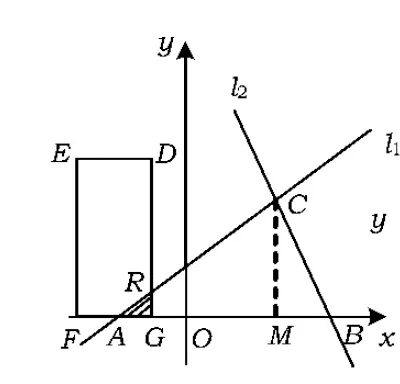
图10
③当8≤t≤12时(如图10),矩形DEFG与△ABC重叠部分为△AGR,则Rt△ARG∽Rt△ACM(当t=12时,为一个点),因此
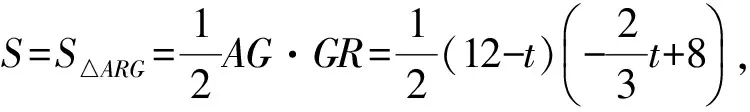
解得
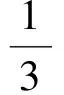
评析本题是一道以矩形的运动构建的集代数、几何于一体的综合题,有一定的难度,是一道具有很好选拔功能的试题.要求学生认真审题,画出不同情况下的图形,根据图形建立时间变量与其他相关变量的关系式,进而构建面积的函数表达式.解决本题的关键是利用矩形在运动过程中产生相似三角形得到待求量与时间t的关系,进而求出面积S与t的函数关系式.
4 圆运动
例4如图11,已知射线DE与x轴、y轴分别交于点D(3,0),E(0,4).动点C从点M(5,0)出发,以1个单位长度每秒的速度沿x轴向左作匀速运动.与此同时,动点P从点D出发,也以1个单位长度每秒的速度沿射线DE的方向作匀速运动.设运动时间为t秒.
(1)请用含t的代数式分别表示出点C与点P的坐标.

①当⊙C与射线DE有公共点时,求t的取值范围;
②当△PAB为等腰三角形时,求t的值.
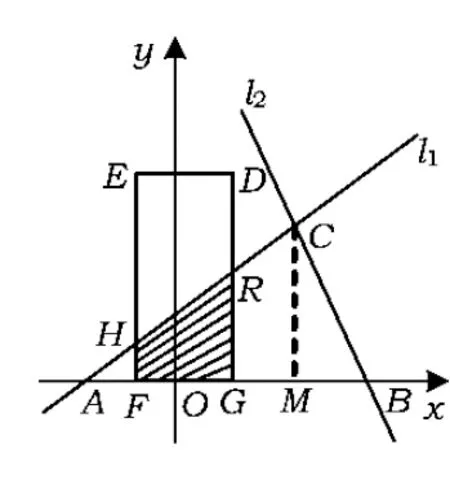
图11
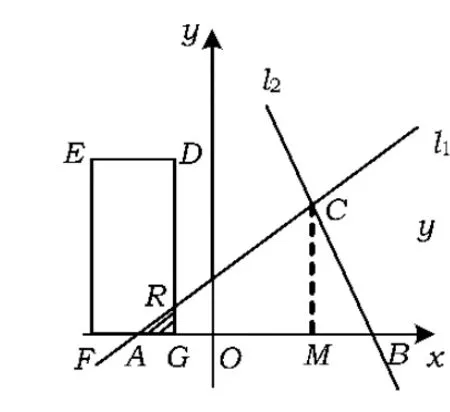
图12
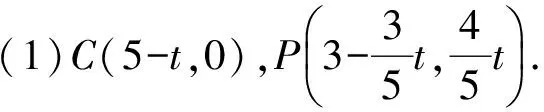
(2)①当⊙C的圆心C由点M(5,0)向左运动,使点A到点D并随⊙C继续向左运动时,有
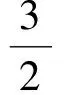
解得
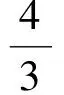
当点C在点D左侧时,过点C作CF⊥射线DE,垂足为F.由△CDF∽△EDO,可得
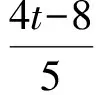
即
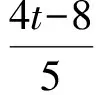
解得
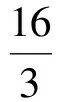
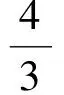
②当PA=AB时,过点P作PQ⊥x轴,垂足为Q,则
PA2=PQ2+AQ2,
即
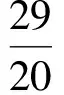
解得
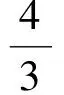
当PA=PB时,有PC⊥AB,因此

解得
t3=5.
当PB=AB时,有
PB2=PQ2+BQ2,
即
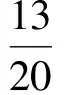
解得

评析此题涉及了代数、函数、圆、等腰三角形等诸多知识点,融入了动态几何的变与不变的特性.解答这类题型的关键是要注意“动静结合、以静制动”,抓住圆与射线有公共点的过程中2个静止的瞬间作为突破口,利用圆在运动过程中与射线形成的相似三角形关系求出t的取值.其重要数学思想“分类讨论”思想贯穿于整个解题过程中.
综上所述,解决运动型试题需要用运动与变化的眼光去观察和研究图形,把握图形运动与变化的全过程,抓住其中的等量关系和变量关系,并特别关注一些不变量和不变关系或特殊关系.同时,要善于应用相似三角形的性质定理、勾股定理、圆的有关性质、图形的面积关系等,并利用方程得到函数关系式.因此,在中考复习中应有意识地加强这方面的训练,培养学生解答动态型试题的能力.

