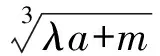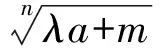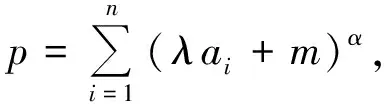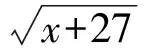一道“希望杯”试题的命题背景和推广

● (杭州外国语学校 浙江杭州 310023) ● (杭州第十三中学教育集团 浙江杭州 310012)

一道“希望杯”试题的命题背景和推广

●朱雪华(杭州外国语学校 浙江杭州 310023) ●周云霞(杭州第十三中学教育集团 浙江杭州 310012)

2010年第21届中学“希望杯”全国数学邀请赛初二第一试试题第6题：

( )

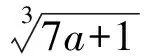
A.p>5 B.p<5 C.p<4 D.p=5

对于初二的学生来说，可以用排除法直接得到答案.爱好数学的学生会询问具体该怎么解答，这引起了笔者的思考.

为此，先给出如下定理：

定理若y=f(x)为D上的上凸函数，满足a+b=c+d且|a-b|≤|c-d|，则

(1)当a=c时,

f(a)+f(b)=f(c)+f(d);

(1)

(2)当a≠c时，

f(a)+f(b)>f(c)+f(d).

(2)

分析由中值定理可知

f(c)-f(a)=f′(ξ)(c-a),其中ξ∈D;

f(b)-f(d)=f′(ζ)(b-d),其中ζ∈D.

不妨假设a≥b,c≥d，则由|a-b|≤|c-d|,得a-b≤c-d.

(1)当a=c时，由于满足a+b=c+d必有b=d，因此式(1)成立.

(2)当a≠c时，由假设易知c>a>b>d,因此ξ∈(a,c),ζ∈(d,b).又f(x)为D上的上凸函数，则f″(x)<0，可知y=f′(x)在D上为减函数，由ξ>ζ,得f′(ξ)

c-a=b-d>0，

于是

f′(ξ)(c-a)

从而

f(c)-f(a)

即

f(a)+f(b)>f(c)+f(d).

易得如下推论：

对于初二的学生来说，只需在x>0,y>0时能证明：

由(a+b-1)3-(a3+b3-1)=3(a+b)(a-1)(b-1)>0，可知式(3)成立.

笔者大胆猜测此题具有如上所述高等数学的背景，同时本文得到的定理和推论在竞赛中也有着广泛的运用.

(2009年全国高中数学联赛试题)

分析此题参考答案如下:

函数的定义域为[0，13].因为

因此

可见,上面的证明也是一种优美的证法.

此类例子不胜枚举，本文所述定理和推论亦是证明此类无理不等式的一种简洁的方法.

[1] 匡继昌.常用不等式[M].3版.济南:山东科学技术出版社,2004.

[2] 叶军.数学奥林匹克教程[M].长沙:湖南师范大学出版社,2009.