新课标高中数学课堂教学中的题型设计
● (富阳中学 浙江富阳 311400)
新课标高中数学课堂教学中的题型设计
●何文明(富阳中学 浙江富阳 311400)
1 数学试卷中的题型
在1978年恢复高考开始的5年里,数学试卷只有解答题(包括证明题和作图题).1981年和1982年都出现了填表题,1983年出现了5道选择题.1984年起,除选择题外,出现了只要求写结果的题型,实质即为填空题(直到1989年才正式命名为填空题).其后二十多年来,这3种题型一直是高考数学试卷的命题形式,只是题量发生了变化.
从2001年起大规模的自主命题开始,高考卷变得丰富多彩,但题型始终没有跳出选择题、填空题、解答题(简称“3种题型”,下同)的圈子.纵观各地会考、阶段考试等,也几乎都采用了这3种题型,各种教辅也不例外.
从应试的角度而言,考试必须便于实施和评判,具备一定的区分度以体现选拔功能.3种经典题型历经多年,渐趋稳定的现状说明它们既适合选拔的要求,又体现了数学的学科特点.首先,数学题答案与思路通常具有确定性,单选题与填空题容易命制,也能够检验考生的知识、思维和能力,并且便于评卷量分;其次,问题作为数学的心脏,它的解决永远不是仅凭直觉,总是可以过程化、具体化、精确化,因此解答题是最具原生态的数学题,最容易考查考生的实际水平,虽然存在一题多解,但解法大多有限,仍便于按步给分.
在数学的课堂教学中,是否也应该严格按照这3种题型进行呢?
2 数学教学中的题型
高中数学课堂教学是数学的再组织、再创造.对学生而言,则是新知识体系的建构过程.从这个角度而言,新课标课本以问题为线索,以问题的解决为主要形式,其模式已经超脱于单纯的解答题范畴,成为广义的题型.而教师通过对问题的分解、重组、复述、引申及铺设台阶,将其转化为易于操作的一个个子问题,每一步几乎都是具体的解答题,这就在课堂中再现了数学发现、发展的虚拟情境.
知识的巩固、应用则基本依赖例题和练习,课本的例题也几乎都以解答题形式展现,课后习题则多以问答题、解答题、实践题形式出现.在实际操作中,教师往往针对概念的理解、知识的澄清、公式的熟悉,设置更多的即兴训练或变式练习,但题型一般都不外乎3种题型.这是数学概念课型的常规处理,原本无可厚非,但是课堂中的题型设置是否一定要与试题相匹配呢?在基本题型之外,是否可能有更适合的题型,以展示知识特点、暴露学生疑问、分散教学难点?鉴于此,笔者产生了如下一些设想.
2.1 设计判断题,暴露理解误区
在必修1方程的根与函数的零点这节课中,由于函数零点的存在性定理的条件“函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0”是结论“f(x)在区间(a,b)内存在零点”的充分不必要条件,其逆命题、否命题均不成立,定理对零点个数的确定也不支持,这都是学生易误解误用之处.因此在定理获得之后,可以设计如下判断题:
例1判断下列结论是否正确,若不正确,请使用函数图像举出反例:
(1)已知函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则f(x)在区间(a,b)内有且仅有1个零点.
(×)
(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)≥0,则f(x)在区间(a,b)内没有零点.
(×)
(3)已知函数y=f(x)在区间[a,b]满足f(a)·f(b)<0,则f(x)在区间(a,b)内存在零点.
(×)
上述判断题的解答,让学生有了及时直面误解的机会,通过反例,从侧面、反面更深入地理解了定理的条件、结论及适用范围.若设置成单选题,将定理本身作为唯一的正确选项,学生在选出正确答案后,容易安于现状,未必愿意深究,因此从认知冲突而言,判断题可能更有效.
2.2 设计连线题,梳理知识关联
在选修2-1或1-1常用逻辑用语中关于命题的否定形式,可以设计如下的连线题:
例2将下列左右2侧互为否定的语句用线段连结:

连线题实质上是多题干对统一题支的选择题,但形式简洁,起到了浓缩的作用.一道连线题可以达到多道选择题的功效.相对而言,连线题的解答具有更广的思维开放性,要求严格界定概念间的关系与区别,容易检验出概念理解的透彻程度.
2.3 设计纠错题,杜绝解题失误
在必修3基本算法语句一课中,学生首次接触编程语言,缺乏感性认识,对其“锱铢必较”的特点不甚明了,很容易出现随意现象.为此,教师现场演示了一些程序出错的例子之后,可以设计如下的改错题:
例3下列语句在输入或执行时都被提示出错,请纠正:
(1)A=B=50; (2)x=1,y=2,z=3;
(3)INPUTx=3; (4)PRINTA+B=C;

纠错题是判断题的延伸,常搭配使用.但对学生的要求更明确,凡是涉及正误判别,或容易发生主观失误的内容,都可以编制,使用尤为广泛.
2.4 设计多选题,防止思维漏洞

图1
在必修5立体几何初步学习之后,鉴于判定定理和性质定理较多,可以设计如下不定项选择题,起到复习整理的作用:
例4如图1所示,给定下列关系,请选择其中尽可能少的作为条件,证明所给的各个结论:
①α∥β;②a∥β;③c∥β;④α⊥γ;⑤β⊥γ;⑥l⊥α;⑦l⊥β;⑧l⊥a;⑨l⊥c;⑩a⊂α;b⊂β;c⊂α;α∩γ=a;β∩γ=b.
(1)要证明α∥β,可以选择条件________;
(2)要证明c∥β,可以选择条件________;
(3)要证明a∥b,可以选择条件________;
(4)要证明α⊥γ,可以选择条件________;
(5)要证明l⊥α,可以选择条件________;
(6)要证明l⊥c,可以选择条件________.
通过一道多选题,简单复习了多种定理,有利于形成对比,也强调了a⊂α,c⊂α等条件的重要性,防止思维漏洞.这样的知识整理,得力于多选题本身的开放性,比单纯的罗列、实际的举例所激发的思维强度大,并且有效.
2.5 设计例举题,鼓励发散思维
函数的综合应用中抽象函数是一类无法回避的问题,为使之具体化,需要学生储备一定的图像知识,培养联想、创造能力.
例5分别用图像列举出满足下面各组条件的函数:
(1)在[0,+∞)上单调递增的偶函数;
(2)图像关于直线x=1对称,在[0,1]和[2,+∞)上单调递增的函数;
(3)图像连续,满足f(0)·f(4)<0且在(0,4)内有3个零点的函数;
(4)满足f(0)·f(4)<0但在(0,4)内不存在零点的函数;
(5)开口向上,有一正一负2个零点的二次函数;
(6)开口向上,在区间[1,2]上恰有1个零点的二次函数;
(7)开口向下,在区间[1,2]上恒大于0的二次函数;
(8)开口向上,在区间[1,2]上恒大于0的二次函数;
(9)开口向下,在区间[1,2]上单调递增的二次函数;
(10)开口向上,在区间[1,2]上单调递增的二次函数.
本例通过学生板书、评议、补充,用直白的题意让学生的思维得到发散的机会,既能促进对函数单调性、奇偶性、零点、二分法等的感性认识,又为解决抽象函数问题、二次函数含参问题打下基础,防止这些题目的隐性条件造成的思维阻隔,让学生在轻松环境下培养“以形促数”的思维习惯.
2.6 设计辩论题,引发深入讨论
在选修2-3排列组合中,平均分配问题是一个易错点,与其教师苦口婆心地教导,不如将2种观点正面摆出,让学生议一议.
例6将a,b,c,d,e,f这6本书平均分给甲、乙、丙3个人,有多少种不同的分法?

像这样的问题组织形式,将认知冲突摆在学生面前,即使无法真的形成激烈的辩论,也至少可以引起学生的兴趣、加深学生的印象.教师视学生情况,完全可以改变数字的大小,降低难度.讨论之后,适时变式为不平均分配及部分平均分配,扩大胜利果实.
2.7 编写应用题,实践“学以致用”
“学习有用的数学”和“养成用数学的习惯”是新课标的理念.能够正确分析题意、建立模型、解数学模型、阐释所得结果的实际意义,这就是实际应用能力.但将一个具体的问题通过简洁而严密的语言整理成一个应用题,则是更高的要求,也才真正能够体现“用数学”.
受时间、设备的限制,当前高中的数学教学依然没有太多机会走出课堂,广泛实践.研究性课题的开展毕竟在时间和参与面上都有较大的限制,不能把“用数学”和锤炼数学语言完全寄希望于偶尔的实践,而忽视了课堂这个主要的学习场所.那么在课堂这样一个“纸上谈兵”式的环境中,怎样才能营造真实、自然的情境,实现“运筹帷幄,决胜千里”?我们作了如下尝试:
准备一只暗箱,其中放置3只白色乒乓球,2只黄色乒乓球,请2名同学按规定次序轮流取球,每次取1只,且不放回,第1个摸到黄球者胜.决出胜负之后将球放回,开始新的一轮.在黑板上记录2人累计获胜的次数,一共进行100次.最终结果显示,先摸的同学胜出的次数为61次,请同学们将此游戏整理成文字,并编写一道涉及分布列的实际应用问题.
规则的描述:暗箱中有3只白球和2只黄球,2种球只有颜色的差别.甲、乙两人依次轮流摸球,每次一只,且不放回,直到摸出黄球为止,首次摸出黄球的为胜方.
问题1设ξ为摸球的次数,求ξ的分布列.




因此ξ的分布列如表1所示.

表1 ξ的分布列
问题2甲与乙谁获胜的概率更大?

问题3摸球次数平均为几次时能决出胜负?
解ξ的期望为

即摸球次数的平均值为2次.
问题4一般地,若有n只白球,m只黄球(n,m∈N*),求P(ξ=k)(k∈N*,且k≤n+1).



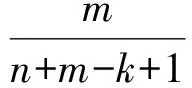




在这个案例中,学生体验了从发现问题到表述问题、设计问题到最终解决问题的完整过程,充分运用了概率与统计知识.
以上7种题型的设置,总的目的,一是用新颖的方式,从正面、反面、侧面等多角度展示知识点的内涵和外延,让学生有一个多方位的理解,可以更通透、更清晰;二是及时暴露学生的理解误区,防患于未然,将易错点直观呈现,引发讨论,加深印象;三是促进课堂的开放性,鼓励学生思考、质疑甚至争论,引起认知冲突,调动学生的求知欲,激活有效思考.
3 题型设计的再思考
3.1 3种基本题型是主体,其他题型为补充
3种题型经过时间和中外文化的考验,事实证明了它们的地位.它们能够很好地呈现大部分教学内容,适当的设计也可以取代上述某些题型,且与试题、教辅相一致,容易编写或者选取,上述题型只是适当的补充.
3.2 其他题型的编纂使用,要注意几个方面
3.2.1 条件充分,科学严密
题目内容的正确性永远是第一位的,所编题目要经得起推敲,不能有知识性的错误.即使是开放性的问题,其切口也要把握牢,让学生易懂、易操作,不超出学生的能力范围,不设计偏题、怪题.
3.2.2 言简意赅,形式优美
在内容正确、表述完整、要求明确的前提下,应力求用语的简练、形式的美观,让学生容易看懂,增强解题兴趣,方便摘抄.
3.2.3 合理选择,不走过场
在等效情况下,还是尽可能选择3种最熟悉的题型,便于学生入手.判断题、多选题、连线题常常可以改成单选题,纠错题、例举题、辩论题也可以转换成解答题,一切以服务教学、服务学生为宗旨.例举题、辩论题在课堂使用中的时间掌控、师生配合上难度较大.若采用了一言堂的处理方法,就无法收到应有的效果,因此要因地制宜,视学生水平和课时数而定,谨慎选用.
3.3 开创发掘更多题型
除上述7种题型外,还可以编写列表题、补图题、多解题、模仿改编题等等.让我们一同努力,丰富课例形式,提高例题与练习的效果.
[1] 罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2001.
[2] 孔德宏,马绍文.美国ACT大学入学考试数学部分介绍及样题[J].数学教学,2006(5):1-6.
[3] 谢绍义.略论数学纠错的教学原则[J].数学通报,2003(10):17-18.
[4] 黄丽生,孙中会.高考《算法初步》的命题趋向与教学建议[J].数学教学,2008(7):12-17.

