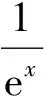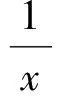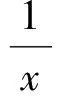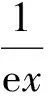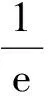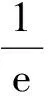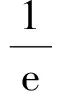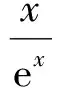从一道联赛题谈导数零点的3类特殊求解策略
● (通州高级中学 江苏通州 226300)
从一道联赛题谈导数零点的3类特殊求解策略
●张春明(通州高级中学 江苏通州 226300)
2009年全国高中数学联合竞赛一试中有这样一道函数题:
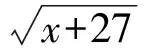
联赛组委会提供的标准答案是巧妙构造系数,利用柯西不等式求解.解答思路尽管精妙,但技巧强、入口窄.其实,还可以利用导数的方法求解,无需太多技巧就可以解决.
解易求定义域为[0,13],且
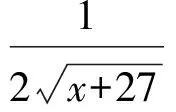
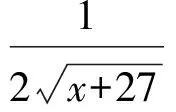
导数是研究函数最值的一个强有力工具.上述解题过程符合高中生的思维习惯,入手容易,运算简单.难点在于求导函数y′=g(x)=0的零点,常规代数解法在这里并不实际,敏锐的“观察力”成为解题的关键.反思高中数学中导数零点的求法,有如下3种较为困难且比较特殊的题型,值得细细品味.
1 零点观察型
已知导数的零点或符号能看出,但利用高中代数方法无法求解.

图1
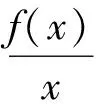
解由g(x)=0,得
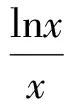
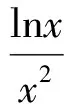
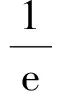
即
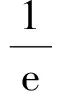
点评导数易求,零点难得,唯“观察”是破解的最优途径.
2 “再次求导”型
这里所讲的“再次求导”有别于二阶导数.“再次求导”是对一阶导数的局部进行二次求导,目的是通过二次求导后的函数的符号变化,判断原函数的单调性情况.
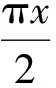
(2009年上海市数学高考理科试题)
解法1(适宜填空题)数形结合,略.
解法2(适宜解答题)
(1)当x=0时,命题显然成立.
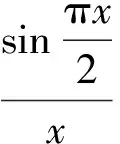
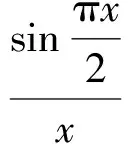


得
g′(α)=-αsinα<0.

g(α) 即 f′(x)<0, 因此f(x)在区间(0,1]上单调递减,得 f(x)≥f(1)=1, 故 k≤1. 点评解法2更具一般性.利用“二次求导”挖出零点,进而实现单调性的判断. 此法常见于利用构造法证明不等式的题型中.当直接构造的函数难以求得零点时,可以整合重组函数表达式,重组的目标是利于求得新函数的零点. 思路1直接构造.令 则 思路2可以适当考虑适度重组整合. 尝试途径1过程表明,此路仍然被卡在零点的得到上,难以奏效(不妨一试). h′(x)=1+lnx, q(x)最大=q(1)=0. 由于h(x)的最小值点与q(x)的最大值点并不相等,因此q(x) 点评“变”的巧,故“求”的简单.2条重组途径看似差异不大,甚至粗看上去途径1更简单,但操作下来却相去甚远.这说明在重组的过程中,要敢于尝试,大胆变形.要选择适合的方案,多想一点,就少算一点. 求导数零点是判断函数性质的前提,文中所提到的3种导数零点的特殊求解策略是高中数学中的难点,也是高考中的热点.深刻理解和熟练掌握,以期发挥导数更大的功能!3 整合重组型