动点问题教学之我见

● (金华市第五中学 浙江金华 321000)

动点问题教学之我见

●施锦华(金华市第五中学 浙江金华 321000)

动点问题是近几年各地中考数学试卷中的一个热点，已成为众多试题中一道亮丽的风景.这类试题的主要特点是一个主题分成若干个小问题，由易到难层层递进，较全面地考查学生的综合理解和分析问题的能力.它区分了学生的综合素质和数学修养，体现了“关注每一个学生的发展”，不同的人在数学上得到不同程度发展的课改理念.下面结合几个典型例题谈谈笔者对“动点问题”教学的看法和体会.

1 数形结合是动点问题教学的灵魂

“数缺形，少直观；形缺数，难入微”.数形结合的思想是研究数学的一种重要思想方法.运用数形结合思想解决“动点问题”就是找准数与形的契合点，根据问题对象的属性，将数与形巧妙地相互转化，以数析形，以形论数，使一些看似无法入手的问题迎刃而解.

(1)直接写出点A，B的坐标；

(2)设点Q的运动时间为t秒，△OPQ的面积为S，求出S关于t的函数关系式；

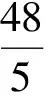
(2009年黑龙江省哈尔滨市数学中考试题)

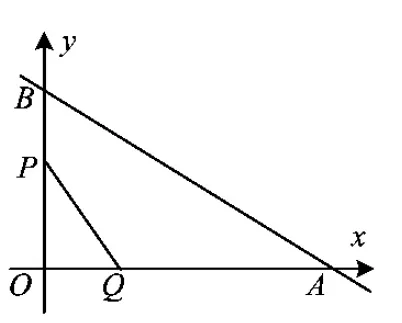
图1

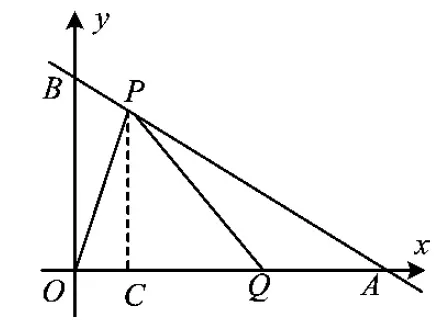
图2

分析(1)A(8，0)，B(0，6).

①当0≤t≤3时，OQ=t，OP=2t,则

②当3

AP=6+10-2t=16-2t.

由△APC∽△ABO,得

于是

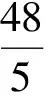
从本例可知，运用数形结合的思想解决“动点问题”可分以下3个步骤：

(1)用含t的代数式表示出含有动点的线段，这一过程要抓住动点所经过的路程来思考，如图1中OP，OQ的表示，图2中AP的表示；

(2)用含t的代数式表示出其他的相关线段，最常见的是通过线段的和差、三角形的相似来达成目的，如图2中PC的表示；

(3)在图形中找到等量关系并根据这些等量关系建立方程或函数模型解决问题.

2 画图分析是动点问题教学的钥匙

解决动点问题的关键是理解图形的运动规律.因此，抓住动点的瞬间状态或相对静止状态，培养学生独立画图分析相对位置关系和形状的变化(形的运动也归结为顶点的运动)，使运动过程直观地展现出来，“动”中捕“静”，以“静”制“动”，是提高解决动点问题能力的基本手段.

例2如图3，直角梯形ABCD和正方形EFGC的边BC,CG在同一条直线上，AD∥BC，AB⊥BC于点B，AD=4，AB=6，BC=8，直角梯形ABCD的面积与正方形EFGC的面积相等，将直角梯形ABCD沿BG向右平行移动，当点C与点G重合时停止移动.设梯形与正方形重叠部分的面积为S.

(1)求正方形的边长.

(2)设直角梯形ABCD的顶点C向右移动的距离为x，求S与x的函数关系式.

(3)当直角梯形ABCD向右移动时，它与正方形EFGC的重叠部分面积S能否等于直角梯形ABCD面积的一半？若能，请求出此时运动的距离x的值；若不能，请说明理由.

(2009年辽宁锦州市数学中考试题)

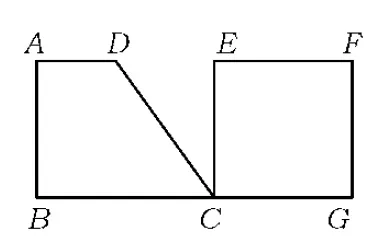
图3

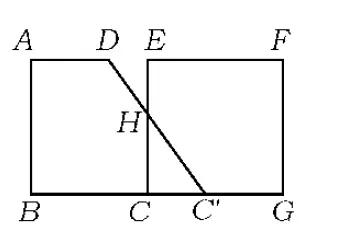
图4

图5

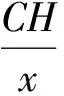
②当4

(3)能；x=5.

画图分析先要“勤”——多画.只有画出特殊位置点处的图形才能确定x的取值范围.例如,本例第(2)小题，画出点D和点E重合时的图形，就能求出分界值x=4；只有画出关键点附近位置的图形，才能找到各种情况下的方程模型或函数模型，例如本例第(2)小题，只有画出图4和图5，才能正确求出相应的函数关系式.

画图分析更要“清”——明晰图形变化的本质.如本例第(2)小题，抓住梯形平移过程中顶点C,D的移动距离一致这一本质特征，就不难表示出DE的长.

3 运用变式是掌握动点问题的途径

运用变式能使问题的本质更为凸显，有利于学生学会从本质看问题，注意从事物之间的联系来理解事物的本质，从而掌握解决动点问题的思路与方法.

运用变式帮助学生理解、掌握动点问题的解题思路，变式的设计要有梯度.例如，在教学例2时,可以设计以下变式：

变式1将条件“当点C与点G重合时停止移动”改为“当点B与点G重合时停止移动”，求出第(2)小题中的函数关系式.

多次尝试后，学生就能画出其余3种情形的图形(如图6～8)，并写出相应的函数关系式.

图6

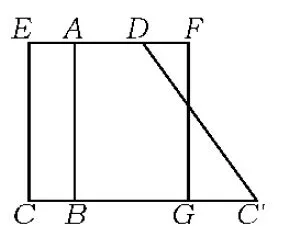
图7

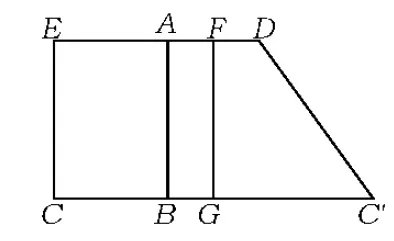
图8

变式2如图9，在△ABC中，∠C=90°，BC=8，AC=6，另有一直角梯形DEFH(HF∥DE，∠HDE=90°)的底边DE落在CB上，腰DH落在CA上，且DE=4，∠DEF=∠CBA，AH∶AC=2∶3.固定△ABC，将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动，直到点D与点B重合时停止.设运动的时间为t秒，运动后的直角梯形为DEFH′(如图10).在运动过程中，△ABC与直角梯形DEFH′重叠部分的面积为y，求y与t的函数关系式.

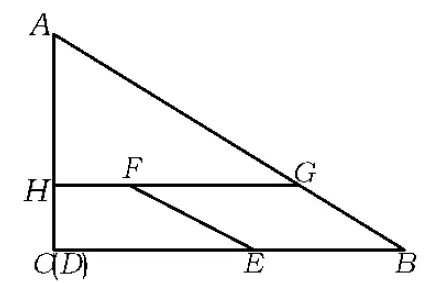
图9

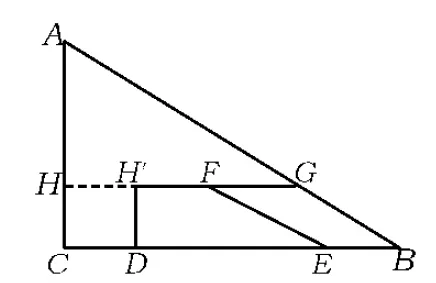
图10

此变式改编自2009年湖南省娄底市数学中考试题，和例2属于同类问题，有较大的相似性，学生经过模仿、思考、尝试，就能进一步熟悉、掌握解决此类问题的方法.

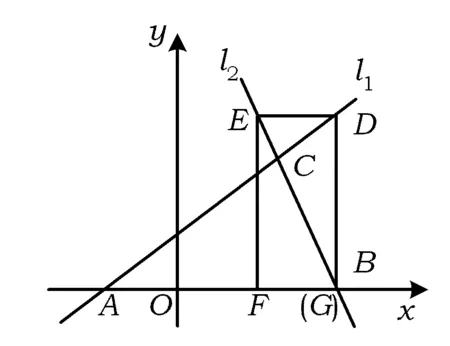
图11

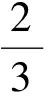
(1)求△ABC的面积；

(2)求矩形DEFG的边DE与EF的长；

(3)若矩形DEFG从原地出发，沿x轴的反方向以每秒1个单位长度平移，设移动时间为t(0≤t≤12)秒，矩形DEFG与△ABC重叠部分的面积为S，求S关于x的函数关系式，并写出相应的t的取值范围.

此变式为2009年山西省数学中考试卷中的题目，在前2个变式的基础上，呈现一个完整的中考压轴题，能给学生一个挑战自我的机会.题型的相似性给学生以一定的信心；题目环境和条件的差别有利于帮助学生脱离单纯模仿的境界，以达到真正掌握应用数学思想方法解决动点问题的目的.

[1] 范鸿．中考数学动点问题中的函数关系赏析[J]．中学数学，2009(18)：35-38.

[2] 吴海宁．动态几何类问题之一——动点型[J]．考试:中考版，2009(3)：21-24.

[3] 于光斌．如何培养学生解答动点、动线和动图问题的解题能力[J]．新课程:教育学术版，2008(7)：126.