矩阵方程Xs+A*X-tA=I的Hermite正定解注记

周裕中， 林利云

(华南农业大学理学院数学系，广东广州 510640)

矩阵方程Xs+A*X-tA=I的Hermite正定解注记

周裕中， 林利云*

(华南农业大学理学院数学系，广东广州 510640)

考虑非线性矩阵方程Xs+A*X-tA=I，其中A是n阶非奇异复矩阵，I是n阶单位矩阵.讨论了该矩阵方程Hermite正定解的特性，改进了以往相应的结论．

矩阵方程； 谱范数； Frobenius范数

考虑非线性矩阵方程

Xs+A*X-tA=I，

(1)

其中A是n阶非奇异复矩阵，A*表示矩阵A的共轭转置,s,t为自然数.最近，许多数学工作者对类似于方程(1)的Hermite正定解作了研究[1-7].

考虑下面的2个一元二次方程

Xs+t-Xt+max(A*A)=0，

(2)

Xs+t-Xt+min(A*A)=0.

(3)

如果A满足

(4)

其中

(5)

那么方程(2)有2个正的实根α2<β1，方程(3)也有2个正的实根α1<β2并且有

0<α1≤α2<ξ*<β1≤β2<1.

(6)

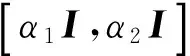
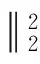
min(X)∪

和

max(X)∪.

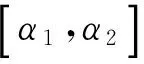
首先给出方程(1)的Hermite正定解的特征值分布情况,证明的过程中需要用到下面著名的Hermite矩阵特征值的乘法扰动定理.

引理1[8]设C是n阶Hermite矩阵,S是n阶可逆矩阵,1(C)≤2(C)≤…≤n(C)是C的特征值,1(S*CS)≤2(S*CS)≤…≤n(S*CS)是S*CS的特征值,则有

min(S*S)k(C)≤k(S*CS)≤max(S*S)k(C)．

∪．

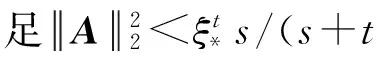
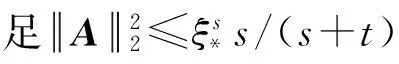
0<α1≤α2<ξ*<β1≤β2<1．

设方程(1)的Hermite正定解X的特征值

0<1(X)≤2(X)≤…≤n(X)≤1，

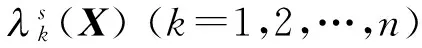
(7)

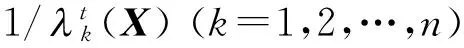
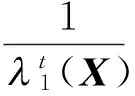
(8)

因此有

(9)

对所有的k=1,2,…,n，由引理1可得

(10)

由Xs=I-A*X-tA和式(7)～(10)，有

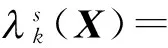
和

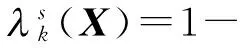
即

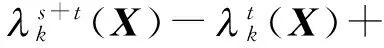
注记1 定理1表明：如果X是方程(1)的Hermite正定解，则X只能是以下3种情形:

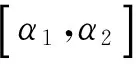
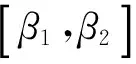
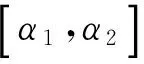
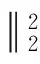
min(X)∪,
max(X)∪．

定理1改进了这一结论.

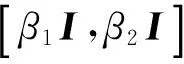
定理2 如果矩阵A满足条件(4)，那么方程

Xs+A*X-1A=I

(11)

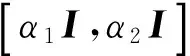
证明当方程(1)中t=1时，条件(4)和条件(5)写成

(12)

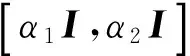
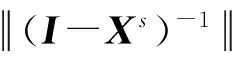
(13)

类似有

(14)

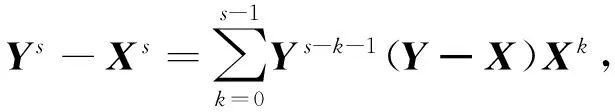
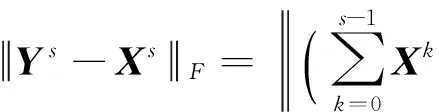
(15)

因为A可逆，所以有Xs+A*X-1A=I和Ys+A*Y-1A=I.从而有

X=A(I-Xs)-1A*,Y=A(I-Ys)-1A*.

(16)

由式(12)～(16)可得

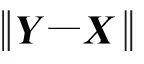
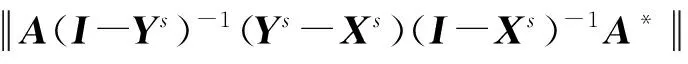
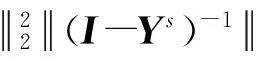
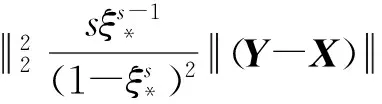
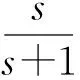
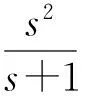
当t≠1时，有下面定理:

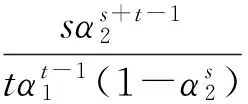
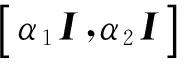
Xt=A(I-Xs)-1A*,Yt=A(I-Ys)-1A*．

因而有

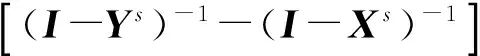
A(I-Ys)-1(Ys-Xs)(I-Xs)-1A*.

(17)

又由

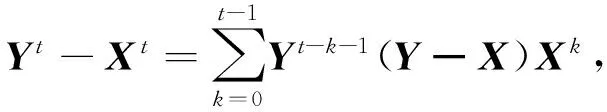
可得

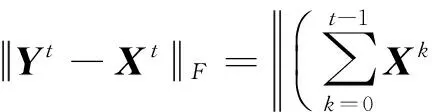
(18)

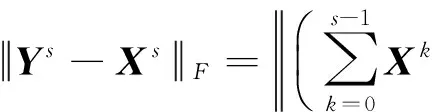
(19)

因而由式(17)～(19)可得

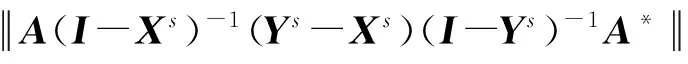
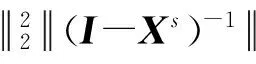
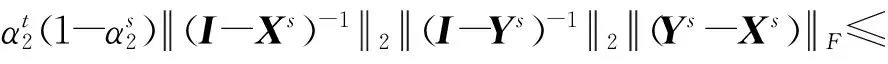
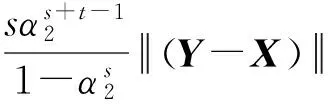
其中第2个等号来源于α2是方程(2)的解，第3个不等式来源于式(19)和

故由定理所给条件可得

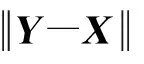
这是一个矛盾.故定理结论成立.证毕.

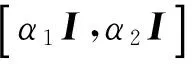
致谢作者对审稿人提出的建议表示衷心感谢.

[1] 陈小山,黎稳.关于矩阵方程X+A*X-1A=P的解及其扰动分析[J].计算数学，2005,27(3):303-310.

[2] ZHAN X.On the matrix equationX+A*X-1A=I[J].Linear Algebra Appl,1996,247:337-345.

[3] XU S F.Perturbation analysis of the maximal solution of the matrix equationX+A*X-1A=P[J].Linear Algebra Appl,2001,336:61-70.

[4] SUN J G,XU S F.Perturbation analysis of the maximal solution of the matrix equationX+A*X-1A=P.Ⅱ[J].Linear Algebra Appl,2003,362:211-228.

[5] LIU X G,GAO H.On the positive definite solutions of the matrix equationsX±ATX-1A=In[J].Linear Algebra Appl,2003,368:83-97.

[6] RAN A C M,REURINGS M C B.On the nonlinear martrix equationXs+A*F(X)A=Q:solutions and perturbation theory [J].Linear Algebra Appl,2002,346:15-26.

[7] ZHANG Yuhai.On Hermitian positive definite solutions of matrix equationX+A*X-2A=I[J].Linear Algebra Appl,2003,372:295-304.

[8] HORN R A，JOHNSON C R.Matrix analysis[M].Cambridge:Cambrdge Uinversity Press,1995.

Keywords： matrix equation; spectral norm; Frobenius norm

【责任编辑 庄晓琼】

ANOTEONTHEHERMITIANPOSITIVEDEFINITESOLUTIONSOFTHEMATRIXEQUATIONXs+A*X-tA=I

ZHOU Yuzhong, LIN Liyun

(Department of Mathematics, College of Science, South China Agricultural University, Guangzhou 510640, China)

The Hermitian positive definite solutions of the matrix equationXs+A*X-tA=Iare studied, whereIis then×nidentity matrix andAis an×nnon-singular complex matrix.Properties of the Hermitian positive definite solutions are investigated,which improves some existing results.

2009-12-10

国家自然科学基金资助项目(10771076)；广东省自然科学基金资助项目(07006700)

周裕中(1969—),男，湖南邵阳人，华南农业大学讲师，主要研究方向：矩阵分析及其应用，Email：zhouyuzhong@scau.edu.cn；林利云(1980—),女，广州梅州人，华南农业大学讲师，主要研究方向：矩阵分析及应用，Email：linliyuan180@126.com.

*通讯作者

1000-5463(2010)03-0004-03

O241.1

A