变量可分离函数的RBF神经网络拟合模型及其VC维

黄榕波， 郭穗勋

( 1.广东药学院数学部， 广东广州 510006；2.广东药学院医药信息工程学院，广东广州 510006)

变量可分离函数的RBF神经网络拟合模型及其VC维

黄榕波1， 郭穗勋2

( 1.广东药学院数学部， 广东广州 510006；2.广东药学院医药信息工程学院，广东广州 510006)

提出变量可分离函数的径向基函数网络拟合模型(Fitting Model based Radial Basis Function network to Variable Separable Function，VSRBF)及其学习算法并分析VSRBF的VC维．VSRBF是一个由多个子径向基函数网络组成的分工协作系统，由于把高维模型分解为低维模型，与传统径向基函数网络(Based Radial Basis Function Network，RBF)相比， VSRBF 不仅明显地降低了系统复杂性而且网络的收敛速度更快. 证明了VSRBF的VC维低于传统RBF的VC维，实验表明VSRBF在处理高维模型的行为明显优于RBF．

分工协作； RBF； VC维

人工神经网络根据输入与输出的样本数据通过学习来拟合输入与输出之间的关系，具有非凡的非线性拟合能力，可以对一个或多个目标同时进行处理. 比如多因素不同水平的实验模型的建立、非线性关系的拟合等，在许多领域得到了广泛的应用[1]. 一般地，当模型的输入因子很多时，为了提高模型的拟合能力，必须增加隐藏层神经元的个数，从而导致模型的系统复杂性的提高，即提高了模型的VC维，系统性能受到影响. 因此降低模型输入维数是目前人工神经网络研究的一个热点．

径向基函数网络(Radial Basis Function Network，RBF)是近十几年来提出的神经网络模型，由于结构简单、学习速度快，在许多领域得到了广泛的应用. 近年来出现了许多关于降低RBF神经网络的输入维数的研究结果. 文献[2]应用独立成分分析(Independent Component Analysis，ICA)和主成分分析(Principal Component Analysis，PCA)降低RBF神经网络的输入维数，结果发现经过PCA技术预处理后模型的性能变差，因为PCA 只用到二阶矩信息，它提取的主因子之间只是不相关而不是独立的，在降维过程中非主因子包含的有用信息丢失了. 而应用ICA提取了RBF的输入因子中的独立成分作为RBF的输入，发现在降低RBF的输入维数的同时RBF的性能得到了改善. 这是因为ICA使用高阶统计矩信息从输入因子中提取独立因子. 然而，ICA抽取的因子是独立成分的近似，仍然会影响模型的性能. 而且如果输入因子彼此独立，ICA无法降低RBF的输入维数．

根据变量可分离特点构建基于径向基函数网络拟合模型VSRBF. VSRBF是一种由多个子RBF组成的分工协作系统，通过把高维输入分解为低维输入作为子RBF的输入，直接降低系统中的子RBF的输入维数，达到降低系统复杂性提高性能的目标．

1 变量可分离函数与VSRBF

1.1变量可分离函数

定义1 设y=f(x)是向量函数，其中

设V的一个直和分解T：V=V1⨁V2⨁…⨁Vq，记

则称向量函数y=f(x)是关于直和分解T的变量可分离函数.

1.2VSRBF的结构及其算法

利用变量可分离的条件构造RBF神经网络拟合模型，VSRBF是一个由多个子RBF组成的分工协作系统. 其结构如图1所示．

VSRBF由输入分解器及q个子RBFr(r=1,2,…,q)组成. 输入分解器把一个高维输入分解成低维输入的直和并分别作为一个子RBF的输入. 即把d维输入x=(x(1),…,x(d))分解成q个低维输入x(r)(r=1,2,…,q)的直和，即：

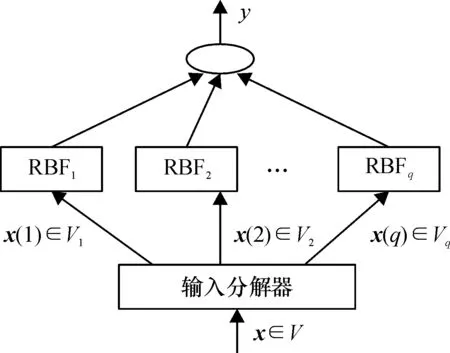
图1 VSRBF 的结构Fig.1 The architecture of VSRBF

x=x(1)⨁x(2)⨁…⨁x(q),

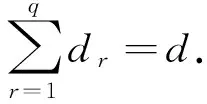
子RBFr(r=1,2,…,q)的输入表示如下：

x(r)=(x(i1),x(i2),…,x(idr))T.

VSRBF的输出等于q个子RBF的输出之和，表示如下：

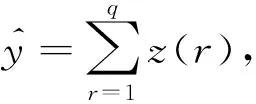
(1)

其中z(r)(r=1,2,…,q)是子RBFr(r=1,2,…,q)的输出．

设训练数据为：(xt,yt)(t=1,2,…,N)，通过最小化式子(2)表示的经验风险函数确定VSRBF中的参数集Θ中的参数．

(2)

其中N为训练数据个数，Θ=Θ1∪…∪Θq,Θr(r=1,2,…,q)分别为RBFr(r=1,2,…,q)的参数集．

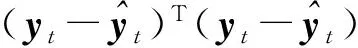
(3)

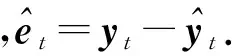
式(3)的详细步骤依赖于RBFr(r=1,2,…,q)模型，这里采用扩展的RBF模型(Extended RBF，ENRBF). 记RBFr(r=1,2,…,q)隐藏层神经元个数为kr，选取核函数φ(s)=exp(-0.5s2)，网络的输出为

(4)

其中

Oj(xt(r))=

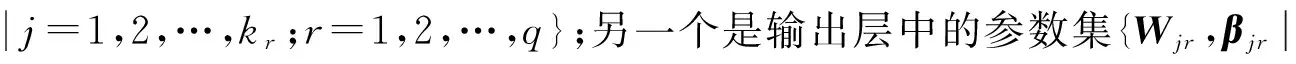
步骤1：通过聚类算法[3]k_mean确定隐藏层参数集{mjr,Σjr|j=1,2,…,kr;r=1,2,…,q}；

步骤2：在最小均方差标准下即最小化式子(2)学习确定输出层参数集{Wjr,βjr|j=1,2,…,kr;r=1,2,…,q}. 详细迭代过程如下：

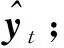
步骤2-2：输出层参数迭代如下：

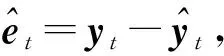
2 VSRBF的VC维

系统复杂性由系统的函数集VC维表示，VC维越高，系统的复杂性越大．

引理1[4]设函数集F是由N个线性无关的函数生成的线性函数集，则：VC(F)=N．

记SVS为VSRBF的函数集；SEN为ENRBF的函数集. VSRBF的参数集ΘVS和ENRBF的参数集ΘEN表示如下：

i=1,2,…,ρVS},

i=1,2,…,ρEN}.

VSRBF与ENRBF的函数集分别如下：

为简明起见，下面均假定网络输出维数为n=1．

定理1 设径向基函网络核函数是确定的，即径向基函网络的隐藏层参数预先确定，ρEN表示ENRBF输出层自由参数的个数,则：

ρEN=kd+k,VC(SEN)=ρEN.

证明ENRBF的输出为：

f(w11,…;w1d,…;wk1,…,wkd,…β1,…,βk,·)=

函数集SEN是下列k(d+1)个函数张成线性函数集:x(i)Oj(x),Oj(x) (j=1,2,…,k;i=1,2,…,d).

由引理1得：

VC(SEN)=k(d+1)=kd+d=ρEN.

定理2 设VSRBF核函数是确定的，即VSRBF的隐藏层参数预先确定，ρVS表示VSRBF输出层参数个数,则：

证明VSRBF的输出为：

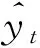
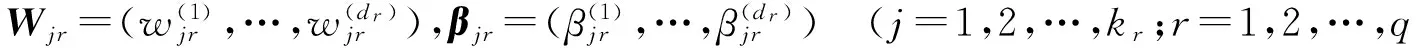
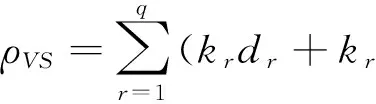
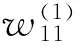
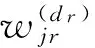
函数集SVS是下列ρVS个函数张成的线性函数集

x(i)(r)Oj(x(r)),Oj(x(r)) (i=1,2,…,dr;

j=1,2,…,kr;r=1,2,…,q).

由引理1有

定理3 设

(1)ENRBF的输入维数为d，隐藏层结点数为k；

(2)VSRBF的q个径向基函数网络的输入维数为dr>0(r=1,2,…,q)，隐藏层结点数为kr>0(r=1,2,…,q). 且

(5)

(3) ENRBF、VSRBF隐藏层参数是固定的；

(4)SEN、SVS分别表示ENRBF、VSRBF的VC维,则VC(SVS)≤VC(SEN).

证明ENRBF输出层参数个数为

ρEN=kd+d.

(6)

把式(5)代入式(6)得：

由定理1和定理2得VC(SVS)≤VC(SEN).

3 实验结果

由下式

y=f1(x1,x2)+f2(x3,x4,x5)+f3(x6,x7,x8,x9)=

sinx1cosx2+x3sinx4-0.4sin2x5+0.5x6cosx7+

0.2x9sinx8

(7)

产生5 100个数据，其中前5 000个数据组成训练集，余下100个数据组成测试集，VSRBF由3个子RBF组成，隐藏层神经元数分别为k1=2，k2=3,k3=3，取学习率为η=0.000 1，扫描训练集200次后收敛，VSRBF和ENRBF在测试集上的行为如图2所示．

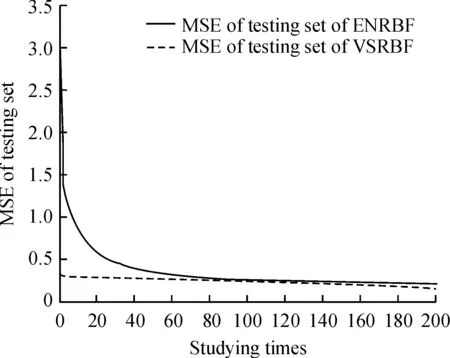
图2 VSRBF和ENRBF在测试集上MSE的比较

Fig.2 The MSE comparison on the testing set between VSRBF and ENRBF

4 总结

VSRBF利用变量可分离特点，把高维问题分解成低维问题，直接降低了系统复杂性，提高了系统的性能. 由于VSRBF的VC维低于ENRBF的VC维，因此学习收敛速度更快．实验表明VSRBF的性能均优于传统的RBF．

[1] DAVEY N, HUNT S P, FRANK R J. Time series prediction and neural networks [J]. Journal of Intelligent and Robotic Systems, 2001, 31: 91-103.

[2] 郭穗勋, 黄榕波. 独立成分分析在径向基函数网中的应用研究[J]. 华南师范大学学报:自然科学版，2004 (3): 42-46.

GUO Suixun, HUANG Rongbo. Study on application of independent component analysis to radial basis function network[J]. Journal of South China Normal University:Natural Science Edition, 2004(3): 42-46.

[3] XU Lei. Rival penalized competitive learning, finite mixture, and multisets clustering[C]∥Proceedings of International Joint Conference on Neural Networks.New York:Institute of Electrical and Electronics Engineers Inc, 1998, II: 2525-2530.

[4] SONTAG Eduardo D. VC dimension of neural networks [J]. Neural Networks and Machine Learning, 1998, 168: 69-95.

Keywords： divide-and-cooperate； RBF； VC dimension

【责任编辑 庄晓琼】

RBFNEURALNETWORKFITTINGMODELTOVARIABLE-SEPARABLEFUNCTIONANDITSVCDIMENSION

HUANG Rongbo， GUO Suixun

( 1. Department of Mathematics，Guangdong Pharmaceutical University, Guangzhou 510006, China;2. College of Medical Information Engineering， Guangdong Pharmaceutical University, Guangzhou 510006, China)

A Radial Basis Function network fitting model to Variable-Separable Function(VSRBF)is presented with its algorithm and its VC dimension is analyzed. VSRBF is a divide-and-cooperate system which is composed of several sub-RBF networks. Since VSRBF decomposes high dimensional model into low dimensional one, to compare with the conventional RBF, its system complexity is reduced remarkably as well as the faster converging speed. It is concluded that the VC dimension of VSRBF is less than that of the conventional RBF, and the experimental result shows that VSRBF performs advantageously comparing with the conventional RBF in high dimensional model.

2010-03-18

国家自然科学基金资助项目(10926191)

黄榕波(1965—),男,广东揭阳人,博士,广东药学院副教授, 主要研究方向：人工神经网络, Email: hrongbo@tom.com.

1000-5463(2010)03-0039-03

TP183

A