Ni掺杂AlN铁磁性的第一性原理研究

曾 坤， 郭志友， 王雨田， 赵华雄, 林 竹

(华南师范大学光电子材料与技术研究所，广东广州 510631)

Ni掺杂AlN铁磁性的第一性原理研究

曾 坤， 郭志友*， 王雨田， 赵华雄, 林 竹

(华南师范大学光电子材料与技术研究所，广东广州 510631)

采用密度泛函理论(DFT)的总体能量的平面波超软赝势方法，结合广义梯度近似(GGA),对Ni掺杂AlN32原子超原胞体系分别进行了几何结构优化,计算和分析了Ni掺杂AlN的结构、能带、电子态密度、集居数及体系总能. 结果表明，Ni掺杂AlN会产生自旋极化，能带结构显示6.25%Ni掺杂AlN呈现半金属性质，有铁磁性，铁磁性可以用Ni和相邻的N之间的p-d杂化机制来解释. Ni掺杂的AlN应该是一种有应用前景的稀磁半导体DMS.

Ni； AlN； 第一性原理； 铁磁性

稀磁半导体被认为是一种理想的制作自旋电子器件的材料，引起了人们广泛的研究兴趣[1]. DIETL等[2-3]的关键性工作使人们的注意力集中到最有可能获得高居里温度的宽带隙的半导体上，他们用基本的铁磁性Zener模型，预言了这些宽带隙的半导体材料的居里温度Tc可能超过室温，如在ZnO、N族化合物半导体，特别是GaN、AlN中掺入过渡金属以形成室温稀磁半导体. 国际上很多实验小组测量中发现在GaMnN居里温度可达800～900 K,AlN中掺入Cr居里温度高于900 K[4-7]. AlN是III族氮化物材料中带隙最宽的，因此AlN基的稀磁半导体具有相当重要的研究价值.

据报导，在Ni掺杂的第一性原理计算中当存在足够的n型载流子时Ni倾向于形成铁磁态[8]. 在实验上, Ni掺杂ZnO已经有不少报道，一些实验表明掺Ni的稀磁半导体有居里温度高于350 K的铁磁性[9-11]. 但是理论和实验上Ni掺杂AlN作为DMS的详细研究鲜有报道. 计算材料学和材料设计允许人们通过理论和计算预报新材料的组分、结构和性能，研究材料的电子结构、表面、界面、光学和结构等性质的本质和起源，以达到从电子层面来设计新材料. 因而计算材料学不仅能模拟试验，提供模拟试验结果，而且可以在制备材料前设计新材料并预测其物性. 第一性原理赝势计算法已经广泛应用于材料模拟[12-13]. 本文采用基于密度泛函理论的平面波赝势法(PWP)对Ni掺杂AlN的32原子超原胞体系进行了几何结构优化计算，并对结果进行了分析，探讨了Ni掺杂的AlN的磁性性质.

1 理论体系、模型和计算方法

1.1稀磁半导体的理论体系

目前稀磁半导体材料的铁磁性起源问题还没有一个统一的理论来处理，最早期人们试图套用稀土金属元素磁性的RKKY(Ruderman-Kttel-Kasuya-Yosida)理论来解释DMSs的磁性. RKKY理论的基本思想是:磁性离子和导带上的电子进行交换耦合作用.

DIETL等人[2-3]提出了平均场的Zener模型，它比较成功地解释了P型的(Ga，Mn)As和(Zn，Mn)Te中的转变温度,揭示了价带中的自旋轨道耦合决定了居里温度的量级和p型的DMSs的易磁化轴的取向. 也正是基于这个模型，DIETL预言了过渡金属掺杂的GaN和ZnO是最有可能实现室温铁磁性的.

SATO和KATAYAMA-YOSHIDA[8]又提出双交换机制去解释铁磁性的起源. 这个理论最初是由Zener提出的，其主要内容是不同价态的磁性离子之间通过“额外”电子进行交换耦合作用. 在DMSs材料中如果相邻的过渡金属原子的磁矩在同一个方向上，那么向上的自旋态之间的杂化作用会使得过渡金属原子的d带宽化. 这些d带上的载流子会降低铁磁结构的能带，使得铁磁序易于生成.

1.2理论模型

本文中所有的计算都是基于AlN超晶胞模型, 如图1a所示. AlN超胞的晶格常数分别为a=b=0.311 nm,c=0.498 nm[14]. AlN超胞中一共有32个原子,掺杂方式是用1个Ni杂质原子去替代AlN超原胞中的1个Al原子,整体掺杂质量分数为6.25%.Ni替位掺杂的超晶胞结构模型如图1b所示.

图1 AlN超晶胞(a)和Ni掺杂AlN超晶胞模型(b)Fig.1 Supercell of AlN (a) and supercell of Ni doped AlN(b)

1.3计算方法

本文的计算工作是由从头算量子力学程序CASTEP Marerical Studio 4.4 软件包中的Castep(Cambridge Serical Total Energy Package)完成[15]. 它始于剑桥大学凝聚态理论研究组开发的一个基于密度泛函理论(density functional theory)结合平面波赝势方法的从头量子力学计算程序. 它主要利用固体物理的Bloch定理处理周期性固态晶格波函数问题，将原本无限多个单电子的周期性晶格简化为只要考虑单位晶格电子的计算.

本文中具体使用CASTEP模块中的方法如下：超软赝势[16], GGA-PBE近似法[17]， Monkhorst-Pack[18]， BFGS算法[19].

2 计算结果和讨论

2.1基本参数

Ni替代AlN超胞中的1个Al原子后，得到的晶格常数为a=b=0.307 nm，c=0.493 nm，比计算纯AlN的得到的a、b分别大0.001 nm,c大0.002 nm. 这主要是由于Ni原子半径要比Al要大，而且Ni的电负性较弱，置换Al原子之后与N形成较强的共价键. 计算得到的N—Ni键长0.195 nm, N—Al键长为0.188 nm. 所以Ni—N键的键长比Al—N键的键长要长，从而增大了晶格常数. 计算得到的N—Ni重叠布居数为0.50，而N—Al重叠布居数是0.61，这说明Ni替代Al，除了键长因此有所增加外，还说明键的共价性相对减弱了.

2.2能带结构

图2给出了质量分数6.25%的Ni掺杂的AlN的自旋极化能带图,费米能级被设定为0.从图中可知，费米面下-8～-1 eV为价带，其宽度大约为7 eV，主要由N的P电子贡献，Ni的d电子也有贡献. 费米面附近的带为杂质带，由掺杂Ni的d电子所形成. 上自旋的能带图中，带隙宽度达到了3.94 eV，和MIWA等的计算4.09 eV比较接近，还是呈现半导体性质[20]. 而下自旋能带发生了分裂，表现出一定的金属性质，因而，整体上(Al，Ni)N呈现半金属性质. 离散的未充满的价带的作用就像是自由空穴一样，因此，在Ni掺杂的AlN中，理论上可实现100%自旋极化载流子的注入. 这表明(Al，Ni)N有可能用作自旋注入.

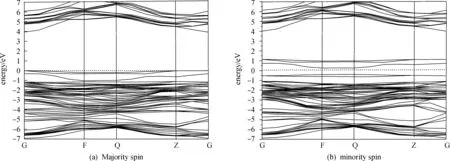
图2 6.25%Ni掺杂的AlN的上自旋(a)和下自旋(b)的能带结构图Fig.2 Band structure of the majority spin and the minority spin of AlN doped with 6.25% of Ni

2.3态密度与铁磁性

下面分析Ni的掺杂对于AlN电子结构的影响.

Fermi面附近的态密度分布往往决定着各种材料的铁磁性质. 如图2所示.自旋向上和向下的态密度分布在Fermi面附近出现了劈裂,这体现了电子的交换相互作用,出现了自旋有序排列. 自旋向上的电子在Fermi面附近有一个大约4 eV的能隙,表现出半导体性，而之所以有金属性是由于向下的电子跨过了Fermi面.综上所述,Ni掺杂的AlN超胞具有半金属性质. 这也与前面能带图的分析结果一致.关于铁磁性的讨论,请看自旋向上和向下的态密度分布存在着一定的差别,这种现象表明此结构存在磁的有序排列.同时在Fermi面附近,自旋向上与向下的电子数并不相等, 这种现象表明有净磁矩,所以整体上Ni 掺杂AlN超胞呈现铁磁性.计算所得的磁距有1.5μB. 考虑稀磁半导体的电子结构，铁磁态可以由齐奈双交换模型或者p-d杂化机制来解释. 图3是超胞中各轨道自旋对净磁矩的贡献，从中可以知道s轨道电子对净磁矩的贡献为0，净磁矩主要来源于超胞中NiN4的Ni的d电子和N的p电子自旋.

图4是超胞中NiN4的Ni的d轨道电子和N的p轨道电子自旋DOS图,费米能级设置为0，正的部分为自旋向上.比较图4a,b,c，d和e可知，对于上自旋来说，Ni-3d和N-2p在-5.5、-4.2、-1.5、-0.5 eV附近重叠或交迭，特别是在-4.2、-1.5、-0.5 eV处几乎是完全重叠的出现非常强的杂化峰，显示了Ni和N之间的非常强的相互作用；对于下自旋来说，费米面上，Ni-3d和N-2p的贡献同样明显，Ni-3d和N-2p在2.8、-0.8 eV重叠或交迭，再参照图3可知,费米面附近的电子态密度主要来自Ni的3d态和N的2p态,且二者的形状极其相似，由此可知它们之间存在杂化作用. 计算表明，在Fermi能级附近的占据态中，对Ni -3d和N-2p的态密度进行积分计算知自旋向上的电子数多于自旋向下的电子数，因此Ni和N的相互作用是铁磁态的，最近邻N原子的2p电子更趋向与Ni的3d电子铁磁序排列. 这些结果表明，Ni掺杂AlN的FM态可以通过p-d杂化机制而解释的.

图4 NiN4的Ni的3d电子(a)和N的p电子自旋DOS图(b,c,d,e)

Fig.4 Spin DOS of Ni 3d (a) and N 2p of the N atom (b,c,d,e) of the NiN4tetrahedron

3 结论

本文采用密度泛函理论(DFT)的总体能量的平面波超软赝势方法，结合广义梯度近似(GGA)，对Ni掺杂AlN32原子超原胞体系进行了几何结构优化，计算和分析了Ni掺杂AlN的结构、能带、电子态密度、集居数及体系总能. 结果表明，Ni替代Al，键长增加，共价性相对减弱了. 下自旋能带发生了分裂，整体上(Al，Ni)N呈现半金属性质. 离散的未充满的价带的作用就像是自由空穴一样，因此，在Ni掺杂的AlN中，理论上可实现100%自旋极化载流子的注入. 这表明(Al，Ni)N有可能用作自旋注入. 另外自旋向上的电子数多于自旋向下的电子数，最近邻N原子的2p电子更趋向与Ni的3d电子铁磁序排列，因而具有铁磁性. 它的铁磁性可以用Ni和相邻的N之间的p-d杂化机制来解释，因此Ni掺杂的AlN应该是一种有应用前景的稀磁半导体DMS.

[1] HU S J, YAN S S, ZHAO M W. First-principles LDA+U calculations of the Co-doped ZnO magnetic semiconductor[J]. Phys Rev B, 2006,73:245205.

[2] DIETL T,OHNO H, MATSUKURA F.Zener model description of ferromagnetism in zinc-blende magnetic semiconductors[J].Science，2000,287: 1019-1022.

[3] DIETL T,OHNO H, MATSUKURA F. Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors[J]. Phys Rev B, 2001,63:195205.

[4] MARK E O,CAMMY R A, STEPHEN J P,et al. Indication of ferromagnetism in molecular-beam-epitaxy-derived N-type GaMnN[J]. Appl Phys Lett， 2001,79: 1312-1314.

[5] REED M L,EI-MASRY N A, RITUMS M K,et al.Room temperature ferromagnetic properties of (Ga, Mn)N[J]. Appl Phys Lett, 2001,79: 3473-3475.

[6] THEODOROPOULOU N, HEBARD A F, OVERBERG M E. Magnetic and structural properties of Mn-implanted GaN[J]. Appl Phys Lett, 2001,78: 3475-3477.

[7] LIU H X, WU S Y, GU LIN,et al.Observation of ferromagnetism above 900 K in Cr-GaN and Cr-AlN thin films[J].Appl Phys Lett，2004,85:4076-4078.

[8] SATO K, KATAYAMA-YOSHIDA H. Electronic structure and ferromagnetism of transition-metal-impurity-doped zinc oxide[J].Physica B， 2001,308:904-907.

[9] SIMAK S I,AHUJA R, ABERG D, et al. Origin of magnetic anisotropy of Gd metal[J]. Phys Rev Lett， 2003, 91：157201.

[10] SCHWARTZ D A,KITTLSTVED K R, GAMELIN D R. Above-room-temperature ferromagnetic Ni2+-doped ZnO thin films prepared from colloidal diluted magnetic semiconductor quantum dots[J].Appl Phys Lett, 2004,85:1395-1397.

[11] 彭坤，周灵平，胡爱平，等. 稀磁半导体Zn1-xNixO的室温铁磁性[J].中国有色金属学报,2007,17(1):35-38.

PENG Kun, ZHOU Linping, HU Aiping, et al. Room temperature ferromagnetism in Zn1-xNixO diluted magnetic semiconductor[J]. The Chinese Journal of Nonferrous metals， 2007， 17(1):35-38.

[12] 陈琨,范广涵,章勇. Mn掺杂ZnO光学特性的第一性原理计算[J]. 物理学报, 2008, 57(2):1054-1060.

CHEN Kun, FAN Guanghan, ZHANG Yong. First principles study of optical properties of wurtzite ZnO with Mn-doping[J]. Acta phys Sin，2008,57(2):1054-1060.

[13] 沈耀文,康俊勇. GaN中与C和O有关的杂质能级第一性原理计算[J].物理学报, 2002,51(3):645-648.

SHEN Yaowen, KANG Junyong. Ab initio calculation of the electron structure of carbon and oxygen impurities in GaN[J]. Acta phys Sin，2002, 51(3):645-648.

[14] ISHIHARA M, LI S J, YUMOTO H, et al. Control of preferential orientation of AlN films prepared by the reactive sputtering[J]. Thin Solid Films, 1998,316(1/2): 152-157.

[15] SEGALL M D,LINDAN P, PROBET M J， et al. First-principles simulation: ideas, illustrations and the CASTEP code[J]. Phys Condens Matter, 2002, 14(11): 2717-2744.

[16] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J].Phys Rev B, 1990, 41: 7892-7895.

[17] JOHN P P, KIERON B,MATTHIAS E. Generalized gradient approximation made simple[J].Phys Rev Lett, 1996, 77: 3865-3868.

[18] HENDRIK J M, JAMES D P. Special points for Brillouin-zone integrations[J].Phys Rev B, 1976, 13: 5188-5192.

[19] FISCHER T H, ALMLOF J.General methods for geometry and wave function optimization[J].J Phys Chem, 1992, 96: 9768-9774.

[20] MIWA K, FUKUMOTO A. First-principles calculation of the structural, electronic, and vibrational properties of gallium nitride and aluminum nitride[J].Phys Rev B， 1993,48: 7897-7902.

Keywords： Ni； AlN; first-principle； ferromagnetism

【责任编辑 成 文】

FIRST-PRINCIPLESTUDYFORFERROMAGNETISMOFNi-DOPEDAlN

ZENG Kun, GUO Zhiyou*, WANG Yutian, ZHAO Huaxiong

(Institute of Opto-Electronic Materials and Technology, South China Normal University, Guangzhou 510631, China)

The geometrical structure of Ni doped 32-atom supercell of AlN was investigated using the ultra-soft pseudopotential method of total-energy plane wave based on the density functional theory (DFT). Band structures, partial density of states, mulliken charges, electron density differences and total-energy of Ni doped AlN crystals were calculated and analyzed in details. The results revealed that the Ni dopants were found spin polarized. Band structures show a half metallic behaviour. The ferromagnetic ground state in Ni-doped AlN can be explained in terms of p-d hybridization mechanism. These results suggest that Ni-doped AlN presents a promising dilute magnetic semi-conductor.

1000-5463(2010)03-0058-04

0641；0649

A