基于思维能力培养的微积分概念教学

周宇剑

（湖南科技学院 数学与计算科学系，湖南 永州 425100）

0. 言

微积分作为描述和处理自然科学、工程技术中实际问题的最准确、最简洁的语言和最强有力的工具,对发展人们的逻辑思维能力、空间想象能力和创造能力起着重要的作用。它以清晰的条理性、严密的逻辑性、高度的抽象性等独特的思维方式和表现形式引导人们在无形中学会解决问题的思维方式、方法。微积分概念的大多数内容融图形、图像、图表、数学符号、文字语言于一体，是培养学生思维能力极好的素材。微积分概念教学宜从以下几方面入手培养学生的思维能力。

1.发矛盾转化的思维，培养辩证逻辑思维能力

逻辑思维包括形式逻辑、数理逻辑、辩证逻辑。形式逻辑的进一步发展即是数理逻辑和辩证逻辑。[1]形式逻辑采用的是自然语言，比较复杂难懂，不易被人们掌握。辩证逻辑则是用运动、变化、发展的观点去研究思维，研究概念、判断、推理的自身矛盾运动和辩证思维的逻辑方法及辩证思维规律等。大学生在中学接触的基本上是形式逻辑和简单的数理逻辑，随着年龄和阅历的增长，他们更需要培养和发展辩证逻辑思维能力。

微积分概念中所蕴涵的认识问题、思考问题、解决问题的方式、方法具有普遍性，符合唯物主义认识论的观点。微积分中有许多充满矛盾的对立概念如有限与无限、曲线与直线、微分与积分、连续与离散、无穷大与无穷小、收敛与发散等。这些矛盾却又能辩证统一的概念促进了微积分的发展与完善。教学中，要善于激发学生思考，积极进行矛盾转化的尝试和实践，促进学生的辩证逻辑思维能力发展。

有限与无限是既有区别又有内在联系的两个对立面，但它们也可以互相转化。例如“1”是确定的有理数，但它可以用一个无穷数列的和：++⋅⋅++⋅⋅⋅来表示；π是个无理数，但它又可以用系列有理数的代数和

一。最让人振奋的是公式“ eiπ+ 1=0 ”的发现，它把两个常用的无理数e与π、虚数单位i、万物的起源数1成功通过简单的运算符号组合成最简单的“0”，实现了有理数与无理数、实数与复数的辩证统一。

极限理论因魏尔斯特拉斯的“ε−δ”语言而获得逻辑严密性。“ε−δ”语言充满着辩证思维，充分体现在用有限量来描述和刻画无限过程，实现了有限与无限之间的矛盾转化。

求曲边梯形的面积的困难就是“曲”与“直”的矛盾，通过把整体的曲边梯形面积分割为局部的小曲边梯形面积之和，由函数的连续性，在小曲边梯形上以直线段替代曲线段，从而把小曲边梯形转化为小矩形，用小矩形的面积近似替代小曲边梯形的面积，再通过求小矩形的面积和的极限而求得曲边梯形的面积。“划分作近似，求和取极限”这种化整为零、积零为整的辩证方法体现了由曲到直的矛盾转化，从而实现了从局部到整体的转化而解决了求任意曲面的面积、不规则立体的体积等实际问题，解决矛盾的思维既直观又形象生动。

又如，在积分中，为了能“凑”微分，dx的形式可以根据题目的需要而千变万化：

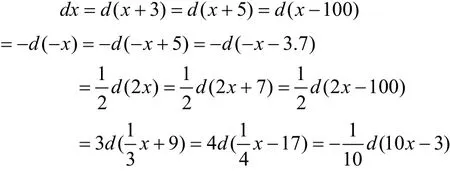
这些矛盾的解决在于辩证逻辑思想的正确引导。由于微积分丰富的辩证思想不是显现在其内容的语言形式上，而是隐含在其概念命题和推理的整体过程中[2]。有时还被成串的逻辑形式掩盖。因此，在教学中，教师要尽可能深入揭示事物内部矛盾，挖掘辩证逻辑思想，并将其延伸到学生的学习、生活中的每一个方面。引导学生仔细品味微积分中解决问题的辩证思维过程及如何通过综合、概括和飞跃式思维解决矛盾。长此以往，潜移默化，就能促进学生的辩证逻辑思维水平的提高。

2.形结合，促进形象思维能力的发展

形象思维是以头脑中的表象作为材料，对表象进行加工的思维过程[3]。它的特征是用形象材料来思维，形象材料最主要的特征是形象性、直观性、具体性。数形结合是形象思维的常见形式，是凭借形和数，经过思维形成概念，再由概念联系形象，进而指导推理、证明、运算的一种思维形式[4]。微积分是描述运动的数学，蕴含丰富的数形结合思想。微积分中的很多问题都体现了形象思维的常见形式——数形化归。微积分中的概念、定理、法则一般都较抽象，学生较难理解。要让学生真正听懂并掌握抽象的微积分概念，离不开数形结合。因此，微积分教学要充分挖掘形象思维的素材，遵循形象思维的规律，给学生充分的思考、观察空间，层层诱导，步步深入，逐步促进形象思维的发展。美国微积分教学改革最具影响的是运用“三原则”讲解微积分基本概念。“三原则”是指:每一个概念以几何、文字描述、代数形式呈现出来。后来“三原则”又发展为“四原则”,在原来的基础上加上“写作”,也就是让学生用自己的语言来表述所学的定理或概念,从而加深对所学内容的理解和认识[5]。其中的1、3项正是我们平时强调的数形结合。

教学中应重视有关概念、定理、法则所反映的几何直观意义与符号表示、文字或口头表述互译能力的培养，帮助学生把抽象的概念“翻译”、“转换”成学生能直接感知、想象或能亲手画出图形的数学形象，借助于形象思维来实现对抽象概念、定理、法则的理解和记忆。促进学生掌握相关概念、定理、法则。

鉴于数学抽象的层次性，可借助于概念的几何意义或几何背景来解释和引入概念、定理及其推论、法则。如连续、导数、微分、积分、定积分、二重积分等概念的引入，可先从几何背景入手，层层递进、诱导，逐步引入，让学生在不知不觉中理解抽象的微积分概念及定理。

如积分上限函数的概念比较抽象、难懂，是学生学习上的一个重点和难点。教学中可由求系列定积分的值与具体图形实例相结合来引入概念。

可由求以下3个定积分值入手：

然后通过定积分的几何意义分析，逐步得到图1：

图1.

再进一步引导学生理解：积分下限不变，每给定一个不同的积分上限值，就有唯一的一个三角形的面积值与之对应。从而引出积分上限函数 y=。通过图像和定积分值的描述，学生很快就能理解积分上限函数的概念。

由于微积分的教学对象是非数学专业的理工科、经济、管理类学生，只要理解概念、性质、定理并灵活运用就足够了，对于它们的证明则可稍作提示，不必花太多时间去证明。如利用几何意义解释定积分的各条性质比给出枯燥的证明更易让学生理解和接受。

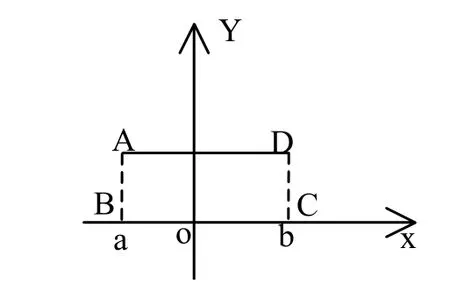
图2.

引导学生观察图2，理解该定积分的值表示x=a，x=b，x轴，函数f(x)=1围成的矩形ABCD的面积值。而这个矩形的一边长为1，另一边长为b-a，所以，矩形的面积值为b-a，从而顺利得出 ∫b1dx =b− a。a再比如通过对函数图像的综合认识，学生积累了有关函数的形象，在此基础上，一气呵成的连贯曲线就是一元连续函数的形象，而二元连续函数的形象则是一张既没有“洞”也没有“裂缝”的曲面。

当然，为了能生动、形象地解析微积分概念、定理、法则，有时可使用多媒体课件，增加直观的数学图形、图像、动画，不仅节约作图时间，而且有利于学生对微积分相关知识的直观理解。

3.重反例、反驳教学，促进创造性思维能力的形成

美国数学家B.R.盖尔鲍姆与J.M.H.奥姆斯特德在《分析中的反例》中指出：“数学由两个大类——证明与反例组成，而数学的发现也是朝着两个主要的目标——提出证明和构造反例进行。”这说明反例反驳思维在数学发现中具有重要意义。反例反驳思想和应用的科学价值同时存在、不容忽视。一个问题能用一个简单的反例来解决，它造成的深刻印象是令人兴奋和备受鼓舞的。反例、反驳作为数学猜想、数学证明、数学解题时的一种辅助和思维的工具，在数学教育方面的意义是值得挖掘和推广的。微积分中最著名的反例就是德国数学家魏尔斯特拉斯于1960年构造的处处连续而又处处不可微的函数：

微积分概念教学中，运用反例、反驳的例子很多。

如判断正误：

（1）无穷大量与无穷小量之积是无穷大量；

（2）无穷大量与有界量的积是无穷大量；

（3）函数y=f(x)在点（ x0， y0）处有切线，y=f(x)在 x0处可导。

直接证明它们的正确与否比较麻烦，但我们采用举反例的方法就简便准确得多。

如当x→∞时，sinx是个有界量，但y =x s inx不是无穷大量，它的极限不存在，所以（2）的结论错误。

又如平面区域D（ p0为D的一个聚点）中的点p以任何方式无限趋于 p0时，函数值都无限趋于某个固定的常数A，才称A为二元函数f(p)当 p →p0时的极限。通过举特殊方式的例子是不能判定二元函数在某点 p0处的极限存在的，但通过反例却可以判定函数的极限不存在。即通过p在D内沿不同路径趋于 p0时，f(p)趋于不同的值，则可判定函数的极限不存在。

反例、反驳教学既有助于学生深入理解有关数学对象的性质，又有助于学生思维的批判性、严谨性和深刻性的发展，促进其创造性思维水平的提高。要举出不同层次的数学对象的反例需要一定的甚至很高的数学修养。寻求反例的过程既需要数学知识与经验的积累，还要充分发挥观察与比较、联想与猜想、逻辑与直觉、逆推、反设、反证及归纳、演绎、计算、构造等一系列辩证的互补的思想方法与技巧。同样一个问题或习题在不同水平的教师或学生手中，具有明显的思维方式与思维深度挖掘的差异。所以，教学中要善于捕捉机会，适时引导学生举出反例反驳相关论点，促进学生的创造性思维能力的发展。

4.重负迁移影响，促进抽象思维的顺利发展

微积分概念中有许多可以通过对概念的正迁移而让学生理解和运用，但也有些概念却不能通过正迁移来实现。教学中要特别重视和强调，不然，学生按常规迁移思维，就会导致对概念公式的错误理解和运用。

研究对象由一元函数增到二元或多元函数时，由于函数自变量个数增加，这种量变就会引起局部的质变，使得二元或多元函数的许多性质与一元函数有着本质的区别。如一元函数在某点的可微性与可导性是等价的，一元函数在某点可导必连续；但二元或多元函数在某点的偏导数即使都存在，也不能保证函数在该点连续和可微。二元或多元函数在某点可微，则函数在该点必连续，且它的偏导数都存在；一阶微分具有微分形式不变性，而高阶微分却不再具有微分形式不变性；在极限均存在的情况下，和、差、积、商的极限等于极限的和、差、积、商（分母的极限不为零）。而函数在某点可导（可微）时，和、差的导数（微分）等于导数（微分）的和、差，但积、商的导数（微分）就不等于导数（微分）的积、商了。

[1]任樟辉.数学思维理论[M].南宁:广西教育出版社,2003.21.

[2]柴冬梅.微积分教学中辩证思维与形象思维的培养[J].成才之路,2007,(17):35-36.

[3]骆川义,刘明杰,孙僵明.文科类专业微积分课程教学中形象思维的应用[J].高等教育研究,2008,25(2):49-52.

[4]庞进生.微积分中数形结合思想的教学探讨[J].周口师范学院学报,2006,23(5):45-47.

[5]高尧来,王世龙. 美国微积分教学改革及其启示[J].理工高教研究,2007,26(3):43-45.