p-群与Abel群的判定

杨 艳

(襄樊学院 数学与计算机科学学院，湖北 襄樊 441053)

p-群与Abel群的判定

杨 艳

(襄樊学院 数学与计算机科学学院，湖北 襄樊 441053)

p-群是有限群中非常重要的一类群，这一点在sylow定理中就得以体现，而pn阶群总是幂零的，因此对pn阶群和交换群的关系可以从两个方面考虑：1)pn阶的群在什么情况下是交换的，并找出相应的类型，2)通过研究群G的sylow子群以判断群G的交换性.

sylow子群；幂零群；p-群；Abel群

群论中，依照群的交换性对群进行分类是很自然也很重要的问题，因此可以把群分为Abel群和非Abel群. 而Abel群的理论作为群论的一个分支本身也具有相当丰富的内容，就像Laszlo Fuchs说过的，群论中很少有性质能够像交换性这样具有深远的影响. 事实上，群论中非常重要的一些概念，如可解、幂零等都是由交换性衍生而来的[1-3].

国内外对于Abel群的研究一直没有停止过，这其中包括对交换性的判定、Abel群的自同构、自由群、有限p-群、可解群、幂零群等诸多问题. Hall. P、Higman. G、Kulikov. L. Ya、Robison. D. J. S等人对这些问题就进行过深入的研究，并取得了很好的结果[4-5].

给出一个群G，判断它是否为Abel群甚至是循环群、有限生成Abel群等是很基础也是很重要的理论.对于不同形式的群，因为它所具有的性质的独特性，通常会找出一些相对应的特别的方法. 同时，也可以从不同的角度对其进行判断，比如它的一些特殊子群、有限群的阶、它的自同构群的结构等. 这部分内容在Abel群理论中是很丰富的.

1 关于p-群的交换性

引理1 非平凡的有限p-群的中心是非平凡的.

定理1 有限p-群是幂零的.

证明：令G是一个有限p-群，且|G|>1，则由引理1可知Z(G)>1， 因此我们可以对群的阶作归纳，即知G/Z(G)是幂零的.

然后做一个自然同态，

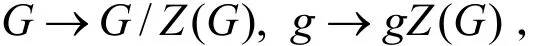
这样可以找到一个G的一个中心列：

定理2 若|G|=p2，则G是Abel群，其中p是素数.

证明：由引理1可知|Z(G)|=p或p2，因此|G/Z(G)|=p或1，即G/Z(G)是循环群，设G/Z(G)=gZ(G)，由此G=g,Z(G)，即G是Abel的.

但当|G|=pn,n≥3时，此定理不一定成立.

例：对称群D8={T,T2,T3,T4,ST,ST2,ST3,ST4}，其中T4=1,S2=1,ST=T−1S，显然|D8|=23，但不是交换群.

接下来重点考察p3阶群的情形.

若群G的阶为p3且G为交换群，则G一定与以下群同构

1) G≅Zp3，此时G为循环群；

2) G≅Zp2⊕Zp;

3) G≅Zp⊕Zp⊕Zp

定理3 若群G的阶为p3且G为非交换群，则G一定与以下群同构：

1) 当p=2时

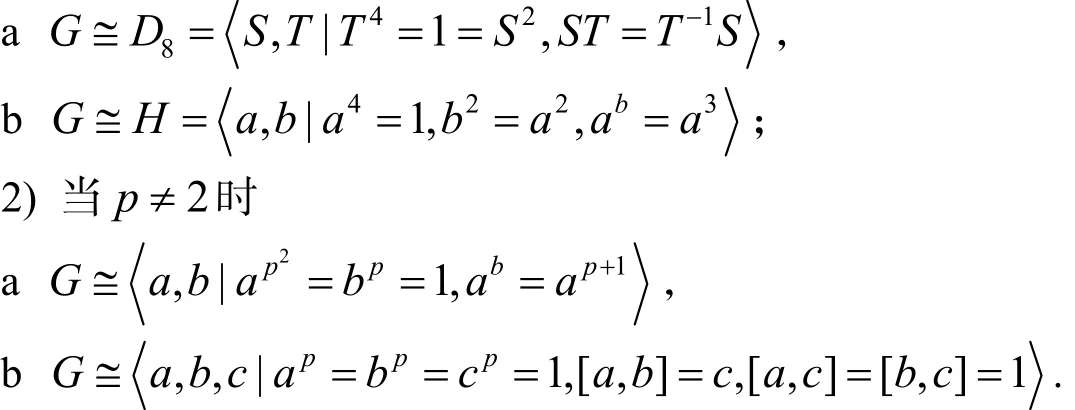
证明：任取G的正规子群N，则因为|G/N|≤p2，G/N为交换群，得

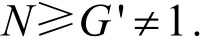
再注意到G中必无p3阶元素，可以分下面两种情形.

设G中有p2阶元素a，这时a是G的极大子群，即aG，因为ap是a的特征子群，所以apG，由前面的分析知G'=ap

1111取i满足ik≡1(mod p)，令b=b1i，则有

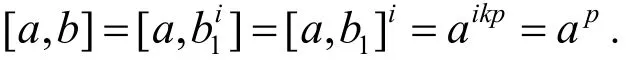
于是G有关系

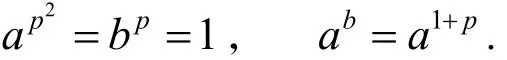
b1的阶不为p. 因为b1p∈a，可令b1p=akp，如果p≠2，则由

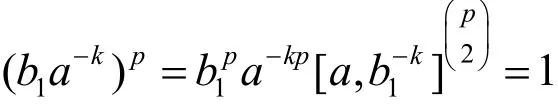
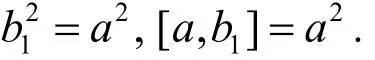
这时以b代b1，得G有如下关系式

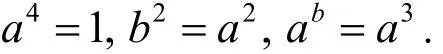
G中无p2阶元素.

若p=2，由G的指数为2可知G一定是交换群.

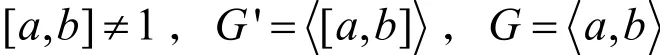
令c=[a,b]，这时有

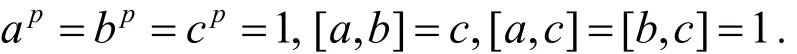
2 Sylow子群与群的交换性

引理2 设G为有限群，A为G的极大交换子群，则A=CG(A).

证明：若CG(A)>A，取x∈CG(A)，令B=x,A，则B交换且B>A，，矛盾于A的选取，故A=CG(A).

引理3 G为幂零群，若H

定理4 设G幂零，则G交换当且仅当对每个sylow子群的极大子群A有CG(A)=NG(A)

证明：必要性显然成立，下面证明充分性.

设P为G的任一sylow子群，A为P的极大子群.则由CG(A)=NG(A)，可知A交换. 若P不交换，则A为P的极大交换子群，由引理2，A=CP(A)=NP(A). 再由引理3，知P=A，矛盾，故P交换，又G幂零，由P的任意性，G交换.

[1] ROSE JOHN S. A Course on Group Theory[M]. Cambridge: Cambridge University Press, 1978.

[2] DEREK J S ROBINSON, GEHRING F W, AXLER SHELDON. A Course in the Theory of Groups[M]. New York: Springer, 1995.

[3] WARFIELD R B. Nilpotent Groups[M]. Berlin: Springer, 1976.

[4] LASZLO FUCHS. .Abelian groups in Hungary [J]. Rocky Mountain J. Math., 2002, 32(4):1181-1195.

[5] CURRAN M J. The automorphism group of a non split metacyclic p-group[J]. Arch. Math. (Basel), 2008, 90(6): 483–489.

Judgment of p-Group and Abel Group

YANG Yan
(School of Mathematical and Computer Sciences, Xiangfan University, Xiangfan 441053, China)

p-subgroup of a finite group is a very important group which can be seen in Sylow theorem . And we know that p-group is nilpotent, so the relation of p-group and Abel group can be considered from two aspects. One is when p-group is abelian. The other is to judge the group is abelian or not through the study of sylow-subgroup of a group.

Sylow subgroup; Nilpotent group; p-group; Abel group

O157

A

1009-2854(2010)11-0017-03

(责任编辑：饶 超)

2010-10-27

应用数学湖北省重点实验室开放基金资助

杨 艳(1981— ), 女, 湖北襄樊人, 襄樊学院数学与计算机科学学院讲师.