刻度平方误差损失下Pareto分布参数的E Bayes和多层Bayes估计

孙 波，罗文强，樊孝菊

(1.襄樊学院 数学与计算机学院，湖北 襄樊441053；2.中国地质大学 数学与物理学院，湖北 武汉430074)

刻度平方误差损失下Pareto分布参数的E Bayes和多层Bayes估计

孙 波1,2，罗文强2，樊孝菊1

(1.襄樊学院 数学与计算机学院，湖北 襄樊441053；2.中国地质大学 数学与物理学院，湖北 武汉430074)

在对给定容量为n的一个Pareto分布样本X1,X2,⋅⋅⋅,Xn,在刻度平方误差损失函数下,利用先验分布讨论Pareto分布参数λ的E Bayes估计和多层Bayes估计.

Pareto分布；刻度平方损失函数；E Bayes估计；多层Bayes估计

Pareto分布是意大利经济学家Pareto将其作为一种收入分布而介绍的，一个多世纪以来，它不仅在经济收入模型中得到应用，在其它领域中也得到广泛的应用.通常用它来描述各种社会经济、物理以及生物现象.例如城市人口、股票价格、保险风险、商业失效、江河流量和某种药理过程后病人的存活时间.在军事领域、天文领域也得到一定的应用. 文献[1]研究了刻度平方误差损失下Pareto分布参数的Bayes估计. 由于推断分布参数的Bayes估计时必须要有确定的先验分布，而某些情况下我们没有办法知道先验分布参数的精确值.本文采用E Bayes和多层Bayes估计两种方法在刻度平方误差损失函数下讨论Pareto分布参数估计的问题，有效的弥补了这一缺陷.

1 Pareto分布和刻度平方损失函数

1.1 Pareto分布

若λ>0，a>0 为实数，则由密度函数f(xλ)=λαλx−(λ+1)确定的分布为称为Pareto分布.其中λ为参数，a>0为已知常数，X1,X2,⋅⋅⋅,Xn是容量为n的简单随机样本，x1,x2,⋅⋅⋅,xn为其观测值，则有

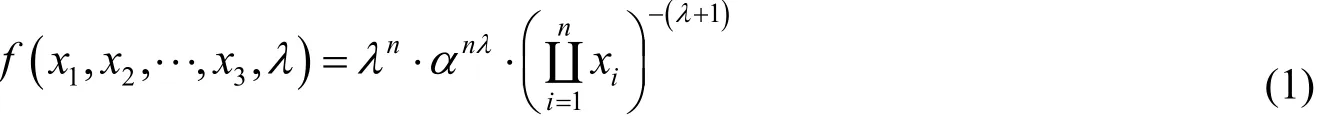
1.2 刻度平方损失函数

决空间中的一个估计，可知L(θ,δ)关于δ的二阶导数为2θk>0，则这个损失函数关于δ是严格凸的， 从

k

而在刻度平方损失函数下，Bayes估计是唯一的. 且在δ=θ处取得唯一的最小值.

2 λ的E Bayes估计

定义1 设样本服从密度函数为f(λ,x)的分布，λ的先验分布为π，其中(a,b)∈D称为超参数，(a,b)的分布为π(a,b).如果λˆ(a,b)是在损失函数LE(λ,δ)及先验分布π下的Bayes估计，λEB(a,b)=

2.1 先验分布超参数的选取

引理1 在刻度平方误差损失函数下，对任意的先验分布，θ的Bayes估计为

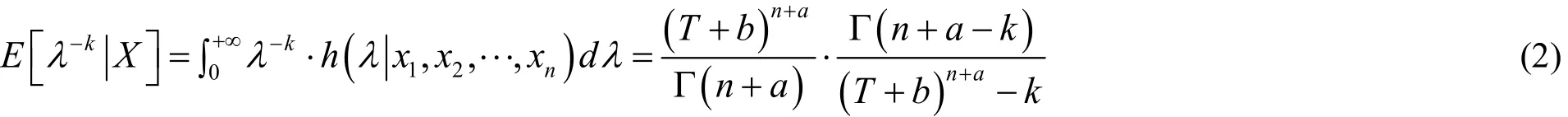
从而得到先验分布取Gamma分布，在刻度平方误差损失函数下，Pareto分布参数的Bayes估计为其中则有定义知刻度损失函数下的E Bayes估计为

3 λ的多层Bayes估计

定义2 设样本服从密度函数为f(λ,x)的分布以及参数λ的先验分布为超参数服从密度函数为π(a,b)的分布，则λ的多层先验密度为λ的多层后验密度为

那么在损失函数下，以π(λ)为先验分布的λ的Bayes估计称为λ的多层Bayes估计.[3]

定理2 刻度平方误差损失函数下，对于第一层先验分布为Gamma分布和第二层先验分布π1(a)=U(0,1)，π2(b)=U(0,c)，Pareto分布参数的λ的多层Bayes估计为

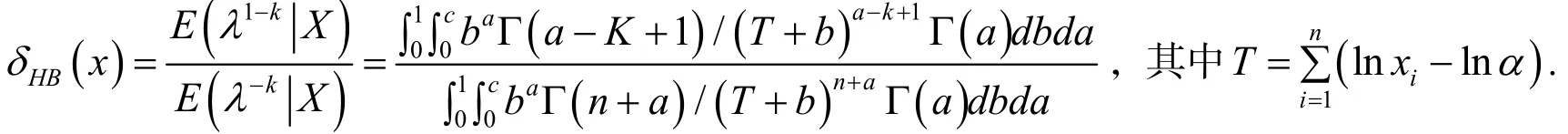
从而参数λ的多层后验密度为

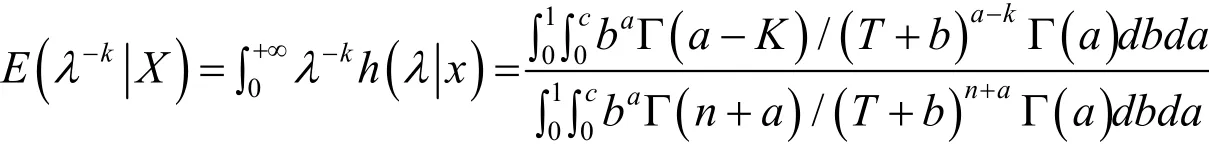
所以有(2)，(3)式得刻度平方误差损失函数(1)下，Pareto分布参数的λ的多层Bayes估计为

孙 波，等：刻度平方误差损失下Pareto分布参数的E Bayes和多层Bayes估计

4 结论

本文采用E Bayes和多层Bayes估计两种方法有效的避免了因无法知道准确的先验分布而不能应用Bayes估计的缺陷，并应用这两种方法对Pareto分布的参数进行估计，分别得出了相应的估计值.

[1] 宋立新, 许俊美. 刻度平方误差损失下Pareto分布参数的Bayes估计[J]. 吉首大学学报, 2008, 29(6): 18-20.

[2] 莱 曼. 点估计理论[M]. 2版. 北京: 中国统计出版社, 2005.

[3] 张琼英. 参数的E Bayes估计和多层Bayes估计[D]. 武汉: 华中师范大学, 2008.

[4] 茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 2版. 北京: 高等教育出版社, 2006.

E Bayesian and Hierarchical Bayesian Estimation of Pareto Distribution Parameter under Scaled Squared Error Loss Function

SUN Bo1,2, LUO Wen- qiang2, FAN Xiao- ju1
(1.School of Mathematical and Computer sciences, Xiangfan University, Xiangfan 441053, China; 2. School of Mathematics and physics, China University of Geosciences, Wuhan 430074, China)

This paper uses prior distribution and study the E Bayesian and hierarchical Bayesian estimation of Pareto distribution parameter under scale squared error loss function w ith a Pareto distribution random sample given.

Pareto distribution; Scaled squared error loss function; E Bayesian estimation; Hierarchical Bayesian estimation

O212.8

A

1009-2854(2010)11-0027-03

（责任编辑：饶 超）

2010-11-20

孙 波(1987— ), 男, 陕西西安人, 中国地质大学数学与物理学院研究生.