岩体弹性模量沿地层埋深变化规律研究
谢向东
(襄樊学院 建筑工程学院,湖北 襄樊 441053)
岩体弹性模量沿地层埋深变化规律研究
谢向东
(襄樊学院 建筑工程学院,湖北 襄樊 441053)
利用国内外关于地应力的实测资料,通过数值方法探讨我国岩体的重要力学参数——弹性模量沿地层埋深的变化规律:10km埋深以上基本是线性增加的,在10km埋深附近会急剧减小. 以丹江口地区为例,依据其表层地应力和岩体弹性模量的试验数据,利用我国岩体弹性模量沿地层埋深的变化规律,反演该区几种主要岩石在不同埋深处的弹性模量.
岩体;弹性模量;水平主应力差;地层埋深
随着对能源需求量的增加和开采强度的不断加大,浅部资源日益减少,许多国家都已进入深部的高应力区进行采矿[1]. 目前,国外许多大型矿山探采深度都在1km以上,最深超过4km[2]. 深部开采工程中产生的岩石力学问题是目前国内外采矿及岩石力学界研究的焦点[3]. 深部岩体处于高地应力、高地温的环境中,所以其力学特性与浅部岩体有很大差别. 近些年来,国内外不少专家学者对不同地方不同种类的岩体进行了高温、高压下的力学性能实验研究,得到了一些很有价值的结论. 但由于实验温度和围压变化范围有限,所以实验结果不能全面的反映深部岩体的力学特性[4]. 研究深部岩体的力学特性,首先要研究其弹性模量随埋深的变化规律. 鉴于此,本文根据国内外实测资料的统计规律性,运用数值方法来探讨深部岩体的弹性模量随埋深的变化规律,以期对国内外的采矿工程起到一定的指导作用.
1 岩体水平主应力差沿埋深变化规律
根据大量的数值模拟,发现岩石弹性模量沿埋深的变化和两个水平地应力(主应力)差沿埋深的变化有一定的对应关系. 为了确定岩石弹性模量沿埋深(本文取地壳浅层20km埋深范围内)的变化规律,下面分三个步骤进行:首先确定两个水平主应力差沿埋深的变化规律;其次探讨岩石弹性模量和两个水平主应力差随埋深变化的关系;最后通过两个水平主应力差沿埋深的变化规律反推岩石弹性模量沿埋深的变化规律.
本文根据以下条件来推断两个水平主应力差沿埋深的变化规律:
1) 德国大陆深钻所得的两个水平主应力差沿埋深(0—25km)变化曲线的形状(图1)[5~7](这是目前国内外最深的钻探资料).
根据图1可以看出:在埋深0—10km范围内,两个水平主应力差是线性增加的,10km—15km达到最大值200MPa—350MPa,然后急剧减小,到15km—25km这个差值基本消失. 这说明当埋深达到15km ~25km时,水平方向的地应力趋于相等.
2) 我国实测水平主应力差的平均值的大小.
目前国内大油田和矿区的地应力实测资料比较多,地域分布也广泛. 2008年,景锋[8]对国内5500m以内的地应力实测资料进行了收集整理,并回归出水平主应力沿埋深变化的表达式,其中最大和最小水平主应力的回归方程为:
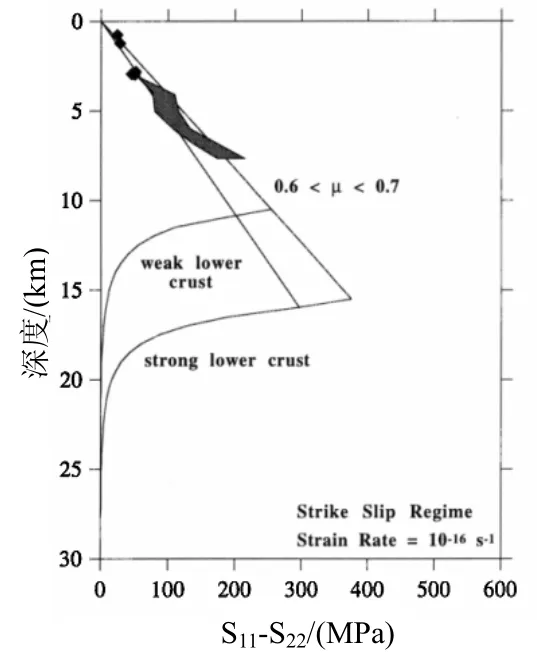
图1 水平主应力差沿深度变化
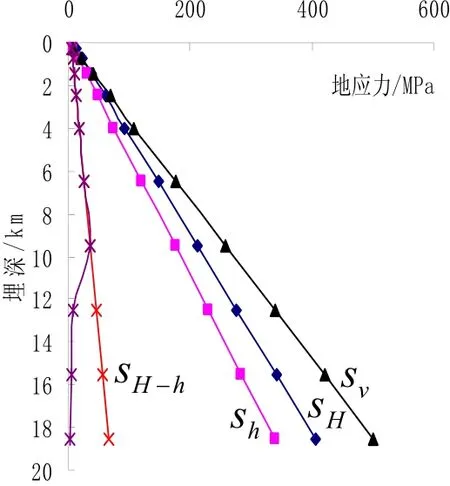
图2 我国平均地应力与埋深关系

根据以上方程绘出平均地应力沿埋深的变化关系如图2所示. 由图2可以看出实测的我国最大水平主应力平均值和最小水平主应力平均值及其差值沿埋深按线性增加,当然这个规律性在5.5km以内是依据实测数据的,而5.5km以下依据上层的规律性. 由图可以看出我国水平主应力的差值沿埋深是线性增加的,在10km深度达到37MPa,这与德国KTB大陆深钻所得差值200MPa—350MPa相差太大. 所以笔者认为我国深部岩体两个水平主应力差沿埋深的变化规律应为图1所示水平主应力差值沿深度变化曲线的形状,只是最大主应力差值减为30MPa—40Mpa(如图2中曲线所示).
2 岩体弹性模量与水平主应力差关系
为了研究岩体弹性模量与两个水平主应力差的关系,本文用有限元软件建立一个长、宽、高分别为200km,200km,20km的模型(图3),在高度方向平均分为十层进行探讨. 模型以辉绿岩为例,岩体物理力学参数为:密度2980kg/m3,弹性模量55.32Gpa,泊松比0.30. 模型的边界条件为:底面约束垂直方向的位移,X轴正面约束X方向的位移,Y轴负面约束Y方向的位移,而X轴负面和Y轴正面施加不同的挤压或拉伸位移,考虑不同的边界位移下S11-S22的变化规律.
工况一:X负面施加120m的挤压位移,Y正面施加50m的张拉位移;
工况二:X负面施加240m的挤压位移,Y正面施加50m的拉伸位移;
工况三:X负面施加挤压位移、Y正面施加拉伸位移分别如图4中(a)、(b)所示.
保持物理力学参数不变,分别计算上述三种工况,根据计算结果绘出S11-S22与H的关系曲线如图5所示. 由图5可以看出如果岩石弹性模量不变,只改变边界条件,那么两个水平主应力的差值沿埋深保持不变. 这说明边界条件的改变只会改变两个水平主应力差值的大小,而不会使其差值大小沿埋深发生变化.
由以上分析推测如果岩石弹性模量沿埋深是变化的,那么水平主应力差沿埋深也是变化的. 所以下面根据图2中水平地应力差沿埋深的变化规律(曲线所示),给计算模型赋予变化的弹性模量(辉绿岩)如表1所示,为了更清楚地表示弹性模量沿深度的变化将表中数据绘于图6中. )

图3 岩石参数反演有限元模型
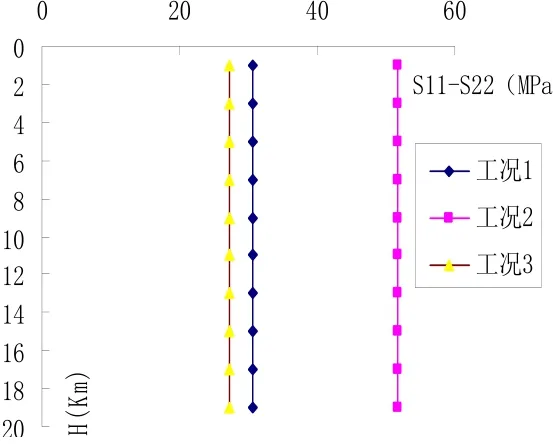
图5 水平主应力差沿埋深的变化
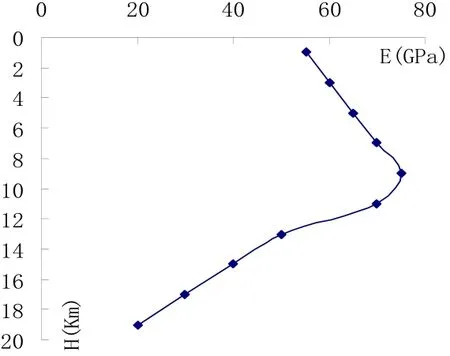
图6 弹性模量沿埋深变化
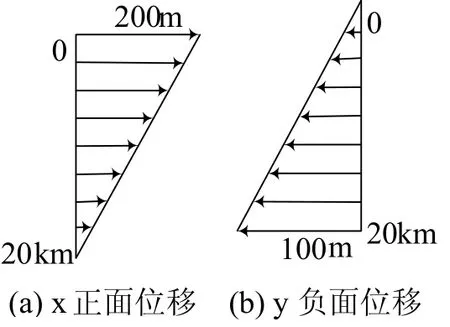
图4 边界位移示意图

表1 弹性模量取值表
取图3所示模型,赋予材料实常数时让弹性模量随深度变化(如图6),而其它实常数不变,施加不同的边界位移,研究S11-S22的值沿埋深的变化规律.
工况一:X负面施加120m的挤压位移,Y正面施加50m的拉伸位移;
工况二:X负面施加挤压位移如图7(a),Y正面施加拉伸位移如图7(b)所示;
工况三:X负面施加挤压位移如图8(a),Y正面施加拉伸位移如图8(b)所示.
对上述三种工况进行计算并将(S11-S22)随埋深的变化绘于图9中,由图可见:不同工况下(S11-S22)—H曲线形状基本相同,且都与E—H曲线十分相似(图6),由此可以认为弹性模量沿埋深变化的曲线形状和(S11-S22)—H曲线形状一致,而边界位移不影响(S11-S22)沿埋深变化的曲线形状,只能整体上改变(S11-S22)值的大小.
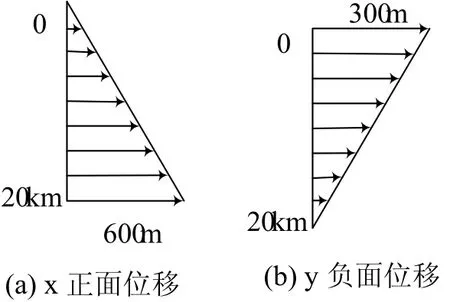
图7 边界位移示意图
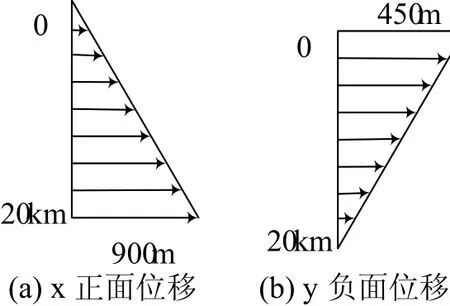
图8 边界位移示意图
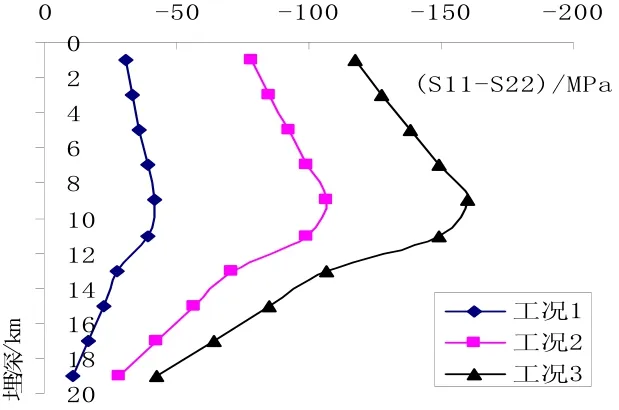
图9 水平地应力差沿埋深的变化
3 岩石弹性模量沿埋深变化规律的确定
根据岩体弹性模量和两个水平主应力差沿埋深有相同的变化规律以及我国深部岩体的两个水平主应力差沿埋深的变化规律,只要知道了表层岩体的弹性模量和两个水平主应力的值,就可以推测同种岩体在不同埋深处的弹性模量. 本文下面以丹江口地区表层(500m埋深内最大水平主应力为17MPa压应力,最小水平主应力为0—10MPa拉应力以及几种主要岩石的弹性模量(来自试验数据)为例[4],采用图2中地应力差值沿埋深变化曲线的形状,来对丹江口地区的几种主要岩石在不同埋深处的弹性模量进行反演.
以辉绿岩为例,调整边界位移和弹性模量参数最终得到一组合理的辉绿岩体地应力资料如图10所示. 与图10地应力相对应的弹性模量即为反演所得的辉绿岩的弹性模量,同样的方法可以得到微风化辉绿岩、碳酸盐岩、砂岩和火山岩的弹性模量沿埋深的取值,下面把反演得到的五种岩石弹性模量沿埋深的取值汇总于表2. 由表2可以看出丹江口地区岩石的弹性模量沿地层埋深10km以上是逐渐增加的,在10km埋深附近会急剧减小. 当然我国其它地区的岩石弹性模量沿埋深的变化可以依据当地的地应力实测数据和表层岩体的弹性模量,利用同样的方法进行反演并确定其大小.
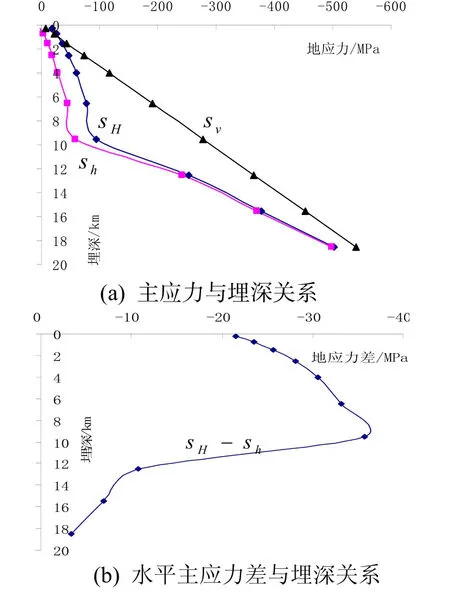
图10 辉绿岩体地应力模拟结果
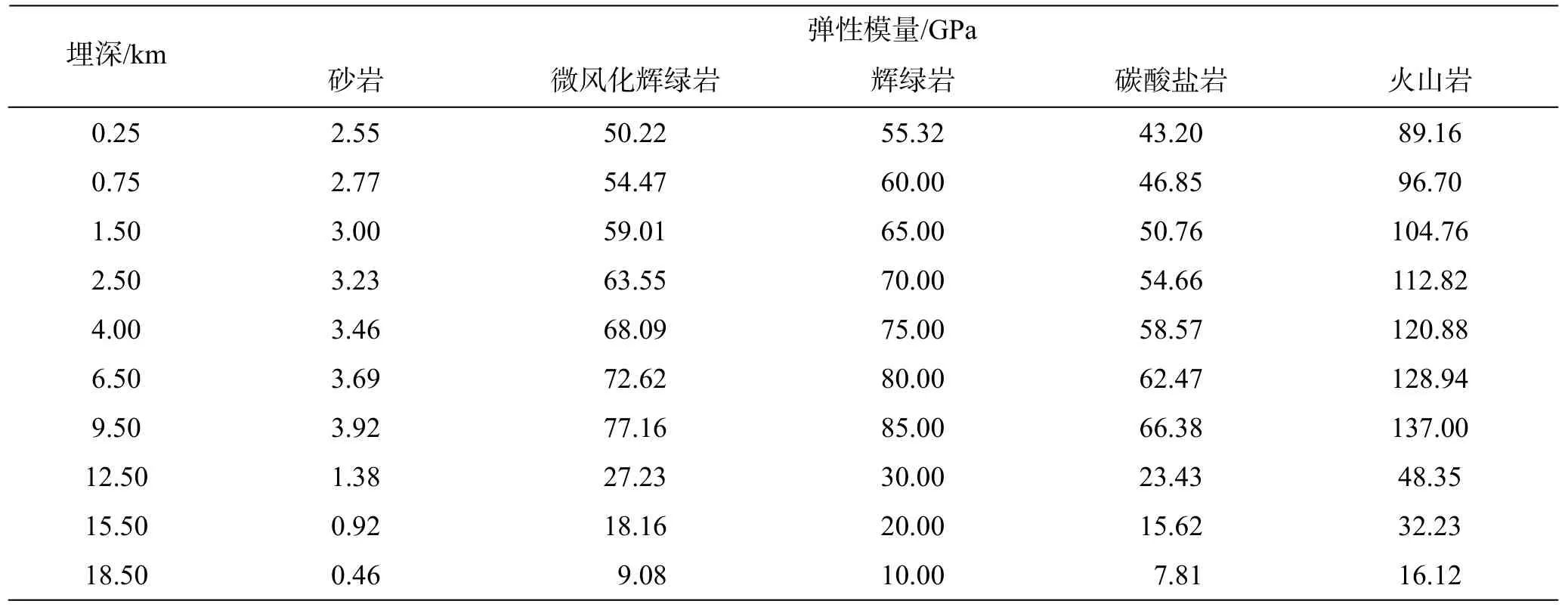
表2 丹江口地区不同埋深处岩石弹性模量
4 结语
本文利用国内外关于地应力的实测资料,通过数值方法探讨了我国岩体的重要力学参数——弹性模量沿地层埋深的变化规律:10km埋深以上基本是线性增加的,在10km埋深附近会急剧减小,这说明10km
埋深附近岩体发生了脆延转化,从而使岩体的水平主应力趋于相等,同时弹性模量也急剧减小. 并以丹江口地区为例,根据其表层地应力和岩体弹性模量的试验数据反演了这一地区几种主要岩石在不同埋深处的弹性模量. 这一推算深部岩体弹性模量的方法对国内外深部开采引起的岩体力学问题的研究具有重要的参考价值.
[1] 康 义, 王恭敏, 孙肇均, 等. 有色金属危机矿山对矿产勘查需求与对策建议[C]//第一届中国探矿者年会论文汇编. 北京: 中国矿业联合会, 2004: 12-18.
[2] 杨志国, 于润沧, 郭 然. 深部高应力区采矿研究综述[J]. 金属矿山, 2007(3): 6-9.
[3] 何满潮, 谢和平, 彭苏萍, 等. 深部开采岩体力学研究[J]. 岩石力学与工程学报, 2005, 24(16): 2803-2812.
[4] 谢向东. 基于流固耦合理论的丹江口水库诱发地震机理研究[D]. 武汉: 武汉大学, 2010.
[5] BRUDY M, ZOBACK M D, FUCHS K, et al. Estimation of the complete stress tensor to 8km depth in the KTB scientific drill holes' Implications for crustal strength [J]. Journal of geophysical research, 1997, 102(B8):18453-18475.
[6] EMMERMANN R, LAUTERJUNG J. The German Continental Deep Drilling Program KTB: Overview and major results[J]. Journal of geophysical research, 1997, 102(B8):18197-18201.
[7] ZOBACK MARK D, HARJES HANS PETER. Injection-induced earthquakes and crustal stress at 9 km depth at the KTB deep drilling site, Germany[J]. Journal of geophysical research, 1997, 102(B8):18477-18491.
[8] 景 锋. 中国大陆浅层地壳地应力场分布规律及工程扰动特征研究[D]. 武汉: 中国科学院研究生院, 2008.
[9] 刘佑荣, 唐辉明. 岩体力学[M]. 武汉: 中国地质大学出版社, 2005.
[10] 陈彭年. 世界地应力实测资料汇编[M]. 北京: 地震出版社, 1990.
Changing Laws of the Young M odulus of Rock Body along Stratigraphic Depth
XIE Xiang-dong
(School of Civil Engineering and Architecture, Xiangfan University, Xiangfan 441053, China)
The changing rules along stratigraphic depth of young modulus of rock body in our country is explored by numerical simulation method, according to the mapping ground stress information in domestic and abroad: basically linear increasing above the depth 10km, and a sharp decreasing near depth 10km.To Danjiang Kou regional for example, the young modulus of several main rock body in different depth was derived, adopting the changing rules of young modulus of rock body in our country along stratigraphic depth and the surface ground stress measured and the test data of rock body young modulus in Danjiang Kou area.
Rock body; Young modulus; Difference of horizontal main stress; Stratigraphic depth
TU375.4
A
1009-2854(2010)11-0009-04
(责任编辑:饶 超)
2010-10-15
谢向东(1975—),男,河南南阳人,襄樊学院建筑工程学院讲师,博士,主要研究方向:工程结构抗震

