蛋白质修正卡方分布函数
王人福,王 星,章社生
(武汉理工大学 统计系,湖北 武汉 430070)
蛋白质修正卡方分布函数
王人福,王 星,章社生
(武汉理工大学 统计系,湖北 武汉 430070)
利用统计分析和数据挖掘的知识,给出了蛋白质残基原子与其他原子的接触距离和接触数的定义,并根据蛋白质的种类的不同,计算了接触距离的数学期望和标准差,得到血红蛋白、激素和肌蛋白残基的概率分布,构造出类蛋白质ASP残基接触数的修正卡方分布函数.
蛋白质;残基;接触数;卡方分布
研究生命科学离不开蛋白质,DNA的生理功能是以蛋白质的形式表达,研究DNA必需研究蛋白质.在新药物的深入开发,蛋白质工程中,人们经常用统计的方法挖掘蛋白质等生命分子的信息特征. 国内外学者从试验、理论和计算等方面对蛋白质进行了大量的研究. 文献[1]对SO2对小鼠肝组织蛋白质的氧化损伤作用及其分子机制进行了实验,得到了蛋白质生命功能的实验数据. 文献[2]根据α-氨基酸和Cα原子的理化特性,研究蛋白质中Cα原子空间拓扑结构,引入Cα原子接触数的概念,讨论了蛋白中Cα原子数目比重、平均接触数以及平均接触数变化率. 文献[3]用数学统计方法计算了两原子之间距离,从蛋白质的数学特征入手,讨论了五类蛋白质的数学特征的分布,指出有进一步研究的必要. 文献[4]通过蛋白质分子内两残基间距的概率分布函数()P r,计算了641个蛋白质分子近程和远程紧密接触对的形成速率,分析了不同蛋白质结构,不同紧密接触对半径以及DNA的绑定时速率的影响. 该文的概率分布函数()P r是半经验的数值计算式,具有构造理论概率分布函数的参考价值. Zhou研究了蛋白质中两原子之间距离的概率分布,在理想气体参考态下,优化出指数为1.61的DFIR函数,其算例表明,DFIR函数有助于构造人工统计能量函数,提高蛋白质设计精度[5]. 在DFIR函数公布以后,有许多文献应用DFIR函数研究蛋白质折叠和设计,以及蛋白质变异等等问题,得到了大量的研究成果. 文献[6-7]应用DFIR函数研究了蛋白质变异和折叠,得到了较好的计算结果. Xu应用DFIR函数预报了DNA核酸类型,其预报精度只有40%,应该有提高的空间[8]. 由于DFIR为指数函数,只用于两原子间距小于20au的工况. 对于更大的间距,需要进一步研究类似于DFIR的概率分布函数.
在文献[2-3]的基础上,本文研究蛋白质原子相互作用,用统计方法研究原子间的距离.
1 数据来源
从RCSB公共数据库中PDB数据库中按蛋白质的种类不同随机选取了三种蛋白质,分别为血红蛋白、激素、肌蛋白. 通过每个蛋白质PDB文件中含有的关于原子名称、原子的坐标以及相对应的残基类型的等信息进行了统计分析.
2 残基原子接触数
2.1 接触数的定义
原子空间位置分布能揭示生命分子中原子的相互作用机理. 在PDB文件中,每一个原子都有空间坐标值. 设第i个原子的空间坐标表示为(xi,yi,zi),第i个原子和第j个原子的空间距离为dij,给定r值,对j求和所得到的值称为第i个原子的接触数:式中,当x<0时,函数δ(x)=1,否则δ(x)=0;ni(r)表示在蛋白质中,所有与第i个原子距离小于r的个数. 给定步长h,ni(kh)表示与第i个原子距离小于kh的原子个数. ni(kh)的差分为d(ni(kh)),对下标i求和,整个蛋白质的接触数
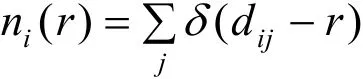
2.2 接触数概率
上面给出了一个蛋白质的接触数的计算公式,则对于任一蛋白质,定义接触数概率:
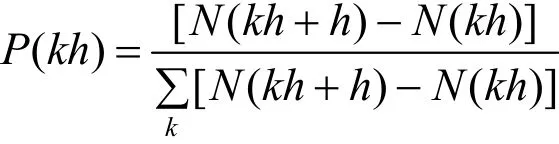
式中,P(kh)表示在所有蛋白质分子中,两原子相距离r落入区间(kh,kh+h)的频率.
若第i个原子限定取蛋白质中残基类型为T的原子,第j个原子遍取蛋白质中的所有原子,则计算出的概率为残基类型为T的接触数概率为P(kh,T,s),s为第s个蛋白质. 于是对于M个蛋白质,残基类型为T的平均接触数概率:
3 结果分析
3.1 血红蛋白
按原子接触数概率随接触距离的分布,不同残基原子的接触距离的数学期望虽然各不相同,但差异很小,大致在31左右波动;并且离散程度即接触距离的标准差也无明显差异,主要集中在17附近. 同时,每种残基对应的接触数概率最大的接触距离也很集中,都在23上下浮. ,可以看出各种残基的接触数随距离分布比较集中,尽管残基中有些原子之间的接触距离超过100,但是总的来说每种残基都有将近91%—94%(具体因残基不同有细微的差异)的原子的接触数的接触距离主要集中在5—60之间. 而且每种残基的接触数的距离分布都非常类似.
3.2 激素
按原子接触数概率随接触距离的分布,不同残基原子的接触距离的数学期望差异较小,大致在29附近,只是残基PRO的接触距离的数学期望值达35.23与其他残基有较大的差距. 同时不同残基的距离分布的离散程度与很相近. 可以看出各种残基的接触数随距离分布比较集中,尽管残基中有些原子之间的接触距离甚至达到100及以上,但是总的来说每种残基都有将近88%—92%(具体因残基不同有细微的差异)的原子的接触数的接触距离主要集中在5—60之间.
3.3 肌蛋白
根据原子接触数概率随接触距离的分布,不同残基原子的接触距离的数学期望相差较小,主要集中在29.6附近. 而且离散程度的差异性也不明显,主要聚集在27附近. 而且每种残基有93%的原子的接触数的接触距离集中在5—60之间,可见各种残基的距离分布不仅很类似而且很集中.
4 接触数的卡方分布
下面开始讨论接触数的卡方分布,残基GLU的概率分布见图1
我们知道自由度为n的卡方分布密度为

设修正卡方分布函数(,)f r n有如下表达式:
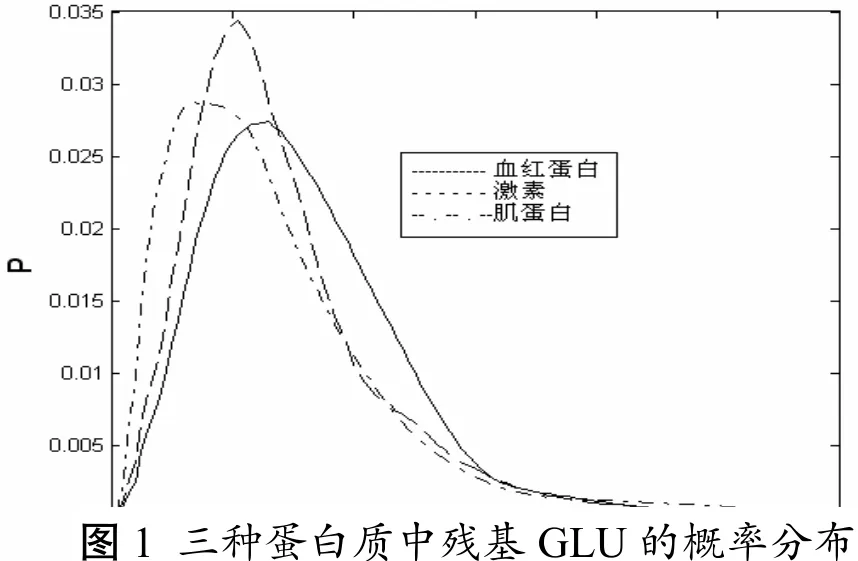
图1 三种蛋白质中残基GLU的概率分布
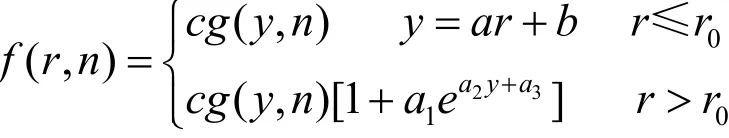
式中有7个未知参数,利用最小二乘思想分段拟合. 先给定卡方分布中的自由度n值;再根据概率密度PT(r)的最大值(此时r=r1)与修正卡方分布函数最大值相等,由此计算出比例值c;再利用最优化的方法拟合得到最优的a和b. 然后计算当r>r1时,第一次实现|f(r,n)−PT(r)|<0.001的坐标r0值. 余下只有三个参数,很容易用最优化方法求出a1,a2和a3的值. 再改变n值,用上面方法重新计算,选取对坐标r=2-120计算误差error=∑|f(r,n)−PT(r )|最小的自由度n的值.
利用以上方法可以分别求出残基为ASP的三种蛋白质的修正卡方分布密度函数:
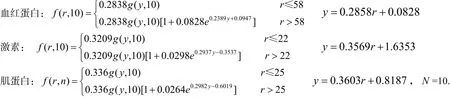
5 结论
根据蛋白质中的原子坐标空间分布,针对血红蛋白、激素和肌蛋白,计算了蛋白质中的原子之间的距离,依据距离的大小值定义了原子接触数,利用PDB文件中的原子坐标数据,计算出接触数的频率及分布,由此构造了修正卡方分布函数,给出了该分布函数的快速优化计算方法. 以ASP残基为例,讨论了血红蛋白、激素、肌蛋白的修正卡方分布函数.
[1] 解静芳, 王学峰, 孟紫强, 等. 1SO2致小鼠肝蛋白质氧化损伤和DNA-蛋白质交联作用[J]. 中国环境科学, 2007(3): 400-403.
[2] 范 宁. 蛋白质Cα原子接触数统计分析及应用[J]. 数字技术与应用, 2010(4): 91-93.
[3] 章社生, 何 康, 范 宁, 等. 蛋白空间结构数字特征统计分析及应用[J]. 武汉工程大学学报, 2010(5): 74-77.
[4] 王向红, 官铬刚. 蛋白质三级结构对蛋白质内部形成紧密接触对速率的影响[J]. 浙江大学学报: 理学版, 2008(4): 400-405.
[5] ZHOU H, ZHOU Y. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction[J]. Protein Science, 2002, 11: 2714-2726.
[6] ZHANG CHI, LIU SONG, ZHOU YAO-QI. Docking prediction using biological information, ZDOCK sampling technique and clustering guided by the DFIRE statistical energy function[J]. Proteins: Structure, Function, and Bioinformatics, 2005, 60: 314-318.
[7] YANG YUE-DONG, ZHOU YAO-QI. Ab initio folding of terminal segments with secondary structures reveals the fine difference between two closely-related all-atom statistical energy functions[J]. Protein Science, 2008, 17: 1212-1219.
[8] XU B S, YANG Y D, LIANG H J, et al. An all-atom know ledge-based energy function for protein-DNA threading, decoy discrim ination, and prediction of transcription-factor binding profiles[J]. Proteins-structure function and bioinformatics, 76: 718-730.
Protein M odified Chi-square Distribution Function
WANG Ren-fu, WANG Xing, ZHANG She-sheng
(Department of statistics, Wuhan University of Technology, Wuhan 430070, China)
Using statistical analysis and data m ining, the definition of contact distance and contact number between residue atoms is given in proteins. According to the different types of protein, the mathematical expectation, standard deviation, and probability distributions of proteins residues are discussed. With least square fitting method, a modified chi-square distribution function of ASP residue is constructed.
Protein;Residue;Contact number;Chi-square distribution
O213
A
1009-2854(2010)11-0024-03
(责任编辑:饶 超)
2010-11-20
王人福 (1991— ), 男, 浙江省衢州市人, 武汉理工大学统计系助理研究员.
王 星(1988— ) , 男, 湖北省荆州市监利县人,武汉理工大学统计系助理研究员.

