经济学的数理分析框架——以市场模型为例

周高宾

(广东金融学院 经济贸易系，广东 广州 510520)

经济学的数理分析框架
——以市场模型为例

周高宾

(广东金融学院 经济贸易系，广东 广州 510520)

数理经济学主体框架分为静态、比较静态和动态三大部分. 每一部分的侧重点各有不同，静态是求解模型均衡解；比较静态关注模型均衡解如何随系统参数扰动而变动；动态侧重均衡解是否能达到及如何达到. 文章以线性局部市场模型为例，分别从静态、比较静态和动态三方面剖析了数理经济分析的整体框架与思路.

数理经济学；静态分析；比较静态分析；动态分析

数学与经济的关系在某种意义上可以抽象成e=f(m)和m=f(e)，其中e代表经济学，m代表数学，两个学科的发展联系密切. 其中e=f(m)表明数学的发展有利于促进经济学的进步，体现在数学为经济分析提供了更严谨的分析技术，每一次数学领域的发展，相应的新思维与工具在经济领域的应用都将极大的推动经济学的发展[1]；m=f(e)表明经济学科的发展也增加了对数学工具的需求，从而引起数学工具的供给增加，推动数学学科的发展. 对经济学科而言，更关注数学学科对经济学科的影响. 现代经济学与传统经济学的主要区别之一是分析经济问题语言的不同，传统经济主要通过文字或几何语言说明与分析经济问题，而现代经济学则更注重利用数学模型刻画和分析经济现象. 单纯从语言层面来看，文字逻辑和数学逻辑并无实质差别，但相对而言，数学语言较少产生歧义，使用数学语言的经济学更加确切地表明经济原理的含义，减少理解上的歧义. 数理经济学便是数学与经济学的一种有机结合，更确切的说，数理经济学不是经济学的一个学科分支，而是一种经济分析方法，是利用数学语言描述经济问题，运用已知的数学定理进行推理的一种方法. 相对于文字描述而言，数学方法有以下优点：首先，便于推理，且表述更加言简意赅；其次，可以应用大量的数学定理，推导出直觉无法直接感知到的经济规律；最后，可更好地从定性的角度上分析经济问题. 因此，数理分析方法在现代经济分析中越来越普遍. 经济学的数理分析框架可分为静态、比较静态、动态三大部分，每一部分的侧重点各有不同. 笔者以市场模型为例，分别从静态 、比较静态和动态三个方面剖析经济学数理分析方法的框架与思路.

1 经济学的数理分析框架与思路

在非时间参数的经济模型中，经济系统可抽象为如下方程[2]：

当讨论这种不含时间变量模型时，许多分析的经济问题的答案都可以由方程(1)的解来回答，它的解为：S:Ω→X，其中S(a)={x∈X;F(x;a )=0}解的含义是将每个参数向量映射到系统变量的均衡值的集合.

根据分析时关注的侧重点不同，可以将经济模型分为静态与比较静态.

1.1 静态模型[3]

简言之，静态模型的核心目标是经过求解得到(3)式，具体地说，对于给定的a，模型的解集合是什么，它是否为空，若解集不是空，则它的维数是多少，即关于均衡的存在性与唯一性问题. 下面以线性形式的局部商品市场模型为例阐述.

仅考虑一种商品模型中包括三个变量：商品需求量(dQ)、商品供给(dS)及商品的价格(p). 根据市场均衡条件以及供给需求定理，可以抽象出以下模型：

静态分析(7)式表明：在给定系统参数(,,,a b c d)时系统变量(,P Q)的均衡解为即模型的解存在且唯一. 图1阐述的是静态分析过程. 在系统参数给定的前提下，在P-Q空间得到商品需求曲线1D和供给曲线S，并求解出均衡解1E.

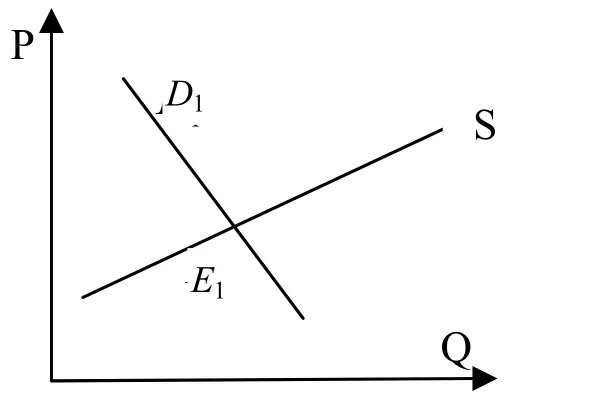
图1 静态分析

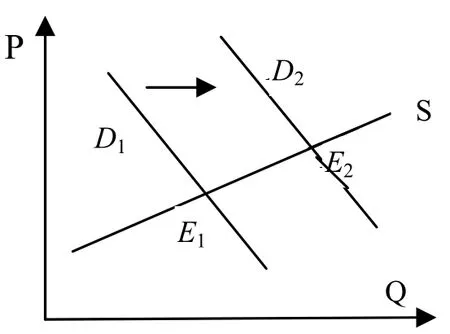
图2 比较静态分析

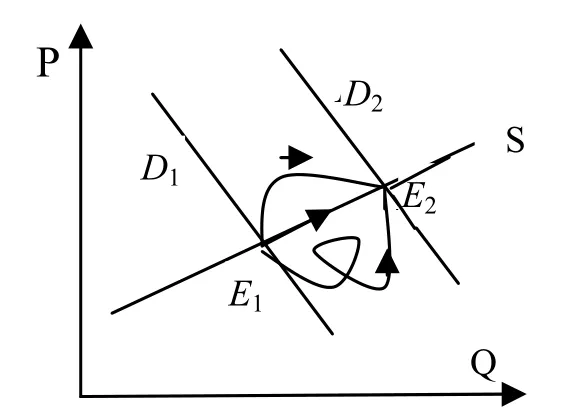
图3 动态分析

1.2 比较静态模型

比较静态中“比较”的含义是新静态均衡与旧静态均衡两者相互比较，在均衡解存在且稳定的前提下，侧重分析随着参数a的改变，均衡解S(a)变化的轨迹[4]. 具体而言，随着系统变量所处的“环境”(a)的改变或某些控制变量的改变，均衡解将沿着什么方向变化，变动的速度如何，分析的实质是求系统变量的均衡解对系统参数变化的比率. 因此，导数(变化率)这个数学概念自然而然的引入到比较静态分析中. 根据S(a)是否能以参数显示表达出来，比较静态分为显函数形式与隐函数形式.

1.2.1 比较静态显函数形式

经济模型经过求解可以得到(3)式，即系统变量xi以显性方式用a表达出来，因此可以直接以系统的参数来表示系统变量的均衡解，系统变量x的解集为S(a). 出于分析的简便，假设只变动系统参数中的一个，其余保持不变，逐次求解∂xi∂ai(实质为偏导)，来描述系统变量所在的“经济环境”(a)的变动对系统变量均衡解的影响，或者说系统变量的均衡解对外来冲击(∂ai)的反映方向(导数∂xi∂ai的符号)与反映速度(导数∂xi∂ai的大小).

−

继续以线性形式的局部均衡商品市场模型为例进行阐述，式(7)中均衡价格p的解S(a)含有四个参数a、b、c、d，可分别解出p−关于四个参数的偏导，并利用已知参数信息判断其符号. 如解出p−关于a的

比较静态分析(8)式表明，“经济环境”(a)的变动对经济系统变量均衡解的影响是均衡价格p−对外来冲

−击(a)的反应方向为正，反应速度为1(b+d)；同理也可以进行均衡数量(Q)的比较静态分析.

1.2.2 比较静态隐函数形式

由于以下两个原因，求解不出系统变量的显函数形式. 现实经济问题中，由于系统变量与系统参数之间的关系复杂且不明确，求解系统变量的显函数形式难度较大. 或系统变量与系统参数之间非完全函数关系(非完全函数关系是指经济分析中抽象出的函数都是对现实经济的一种近似描述，所以有时简约的隐含数F(x;a)=0，反倒是理想的描述方式)，没有必要求系统变量的显函数形式[5]. 因此往往只能得到抽象的方程组(2)，而无法得到方程组(3). 在此种情况下只能进行隐函数形式的比较静态分析——虽然不能得到方程组(3)，但可以利用隐函数定理、全微分等方法，解出∂xi∂ai，并利用已知参数信息来判断∂xi∂ai的大小.

仍以线性形式的局部均衡商品市场模型为例进行阐述，Qd表示需求，P为价格，Y0为收入且是外生参数，需求是价格和收入的函数，且关于价格反向变动，关于收入正向变动. 供给Qs仅是价格p的函数，且供给与价格反向变动. 当无法预知相关函数的具体形式时，根据市场均衡条件和供给需求定理，该问题

进一步假设函数D和S连续且光滑，其中Qd，Qs为系统变量，Y0是系统参数. 令Q=Qd=Qs，并化简，可将市场模型表示为：根据已知可得：F1、F2具有连续偏导且系统变量的雅可比行列式J不为零.

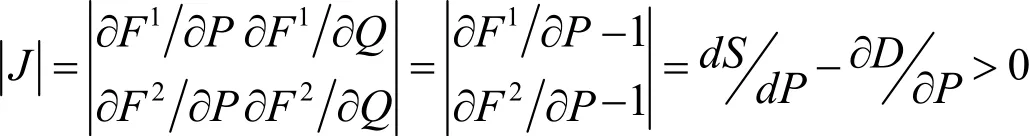
进一步假设均衡解存在(只有存在，比较静态分析才有意义)，根据隐函数定理可得：

−

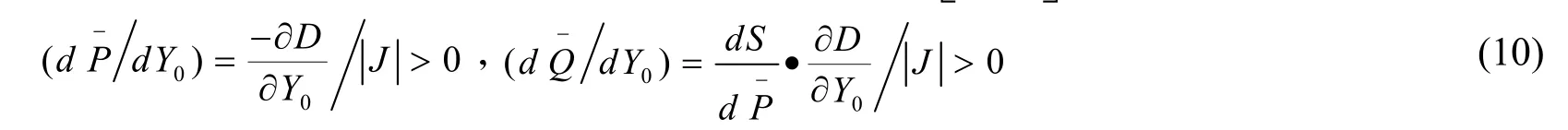
(10)式表明，“经济环境”(a)的变动对系统变量均衡解的影响是：均衡价格P对外来冲击(Y0)的反应方向为正，反应速度为(−∂D∂Y0)J ；均衡产量Q−对外来冲击(Y0)的反应方向为正，反应速度为−(dS d P)*(∂D∂Y0)J . 该结论正是商品需求函数中的命题，即由收入增加造成的需求曲线向上移动会导致更高的均衡价格和更大的均衡产量. 图2所描述的是比较静态过程，当系统参数Y0产生一正向扰动，需求曲线D1移动到D2，均衡点由E1变动到E2.

1.3 动态模型

比较静态研究的是在新均衡有定义且可达到的前提下，侧重分析系统参数变化如何引起均衡的变动，注重对新、旧均衡进行比较，而未涉及旧均衡向新均衡调整的过程，并且调整过程中的时间因素也未纳入分析范畴. 因此，它必然忽略了由于模型内在的不稳定性(内在不稳定性即指系统内变量本身是时间的函数，随时间的变化而变. 这就造成了均衡解稳定与不稳定之分)导致新均衡难以达到的可能性. 那么对调整过程的研究属于动态经济学范畴，此分析思路更加关注变量随时间变化方式及均衡稳定性. 动态分析是在经济系统调整过程所需时间足够长的假设下，系统变量能否调整到均衡水平. 设为系统内变量x的均衡解，且x是关于时间的函数x(t)，当时间足够长是否收敛于，当收敛于则称系统为动态稳定，

−如不收敛于x，则称动态不稳定. 还是以线性形式的局部均衡商品市场模型为例. 在上文的比较静态模型中，其中一条假设是系统内变量在受到系统参数扰动时，经过调整，能达到系统均衡解且稳定. 但是系统变量在调整的过程中，不仅价格随时间变化而变化，而且商品数量也随时间变化. 因此价格和产量都是关于时间的函数，即P(t)和Q(t). 根据市场供求法则，在某一时刻价格对时间的变化率总是与该时刻的超额需求成比例，可得价格关于时间的微分方程：

2 结语

本文分析了静态、比较静态和动态分析的定义及相互关系. 静态是求解模型均衡解，比较静态关注模型均衡解如何随系统参数的冲击而变动，动态侧重均衡是否能达到及运行的轨迹. 本文以简单的线性局部市场模型为例，阐述数理经济分析框架. 静态、比较静态和动态分析作为分析问题的方法，初级和中级经济学多使用静态与比较静态分析方法，如AD-AS模型分析均衡的价格和产出(静态分析)，以及均衡产出与价格如何随外部扰动而变化(AD-AS曲线的移动，比较静态分析)；IS-LM框架是求解均衡利率和产出(静态分析)，以及外部扰动下均衡利率与产出的变动(IS-LM曲线的移动，比较静态分析)；高级经济学更多使用动态方法分析跨期经济问题，例如经济增长、跨期消费、跨期货币需求等. 本文市场模型使用的是单期均衡框架，该框架特征是一个均衡条件和几个行为方程的联立，利用方程组形式对经济现象加以描述与分析.均衡分析关注的是稳态，即价格提供激励，在价格和理性行为主体的“自利之心”指引下，厂商与家庭相互独立地采取策略并最终完成资源的有效配置.[6]虽然理论上的均衡点在经济运行中很难实现，但系统在未达到均衡点之前，系统机制总是保证非均衡点向均衡方向运行. 数理分析在现代经济分析中越来越普遍，但需要明确的是，数理经济学的定量分析方法其目的在于加强我们对经济学定性的理解.[7]

[1] 蒋中一. 数理经济学的基本方法[M]. 北京: 商务印书馆, 1995.

[2] ANGEL DE LA FUEUTE. 经济数学方法与模型[M]. 上海: 上海财经大学出版社, 2003.

[3] 蒋中一. 动态最优化基础[M]. 北京: 商务印书馆, 1999.

[4] 林毅夫. 经济学研究方法与中国经济学科发展[J]. 经济研究, 2001(3): 18-24

[5] 钱颖一. 理解现代经济学[J]. 经济社会体制比较, 2002(2): 54-61.

[6] 田国强. 中国国营企业改革与经济体制平稳转轨的方式和步骤——中国经济改革的三阶段论[J]. 经济研究,1994(11): 6-13

[7] 林毅夫. 本土化、规范化、国际化：祝贺创刊40周年[J]. 经济研究, 1995(10): 8-16.

M athematical Analysis Structure of Econom ics: w ith a Case of Market Model

ZHOU Gao-bin
(International Economy and Trade Department, Guangdong University of Finance, Guangzhou 510420, China)

Mathematical economics consists of three parts: statics, comparative statics, and dynam ics. Each part has its own emphasis. This paper, taking market model as an example, tries to depict the structure of the mathematical method for economy.

Mathematical econom ics; Static analysis; Comparative static analysis; Dynamics analysis

F011

A

1009-2854(2010)11-0013-04

（责任编辑：陈 丹）

2010-09-27;

2010-10-25

周高宾(1979— ), 男, 江西余江人, 广东金融学院讲师, 中山大学博士生, 主要研究方向: 货币金融.

−