让冰冷美丽的“ε-N”极限定义成为火热的思考

董方亮，金为民

（鹤壁职业技术学院，河南 鹤壁 458030）

让冰冷美丽的“ε-N”极限定义成为火热的思考

董方亮，金为民

（鹤壁职业技术学院，河南 鹤壁 458030）

数学具有两重性——火热的思考和冰冷的美丽。数学教育应该把教科书上数学的学术形态化为学生易接受的形式，数学的严谨呈现为“冰冷的美丽”，数学的发现和理解却是“火热的思考”。本文以数列极限教学为例，对体现数学的两重性进行了探讨。

火热的思考；数列极限；建构主义；数学思想方法

数学教育的奠基人、荷兰数学家H.Freudenthal（1908～1990）有一句名言：“没有一种数学思想，以它被发现时的那个样子发表出来。一个问题被解决以后，相应地发展成一种形式化的技巧，结果使得火热的思考变成了冰冷的美丽。”说明数学具有两重性——火热的思考和冰冷的美丽。

然而，当今的数学教学，大多呈现出数学“冰冷的美丽”的一面，忽视了数学的另一面——“火热的思考”。许多数学教学呈现给学生的是精确的定义、严格的程式、缜密的逻辑、高度的抽象，把数学切割为一个个公式、符号、定理、习题，数学留给学生的印象是思维的体操，是一大堆题目，是抽象、散乱、遥远、不可捉摸、不讲道理。从小学到大学，对这样一们不知从哪里来到何处去的课程，许多学生内心的彷徨与无奈有增无减。难怪时常有学生问同样的问题：“学习数学有什么用？” 其实，许多老师也说不清。

随着社会、经济的不断发展，高等数学的应用已渗透到自然科学、工程技术、生命科学、社会科学、经济管理等众多领域，成为解决各种实际问题的工具，特别在经济领域的应用更已日益深入。同时，社会对人们数学素养的要求越来越高，不论他从事何种职业，都需要学习数学、了解数学和运用数学。因此，数学教育应该为更多的学生提供一条理解数学、享受数学、学会数学的途径，教学中应该把数学的学术形态化为学生易接受的形式，在一些基本概念、基本理论、基本定理建立时，不能满足于形式地、演绎地给出，要把数学本质用问题形式、直观形式等揭露出来，经过火热的思考来理解数学，而不是被动地接受定义、定理等结论。在倡导创新教育的今天，火热的思考更为重要。

下面以数列极限教学为例，谈谈笔者的一些做法。

大家知道，高等数学是用极限的理论和方法研究函数的，极限是它的武器和工具, 极限的思想方法贯穿高等数学的始末。而极限概念是一个群体，各概念之间有着紧密的逻辑联系，数列极限又是极限理论的基础，因而更显得数列极限尤为重要。怎样教数列极限，才能使学生真正了解它的直观背景，掌握它的精神实质，理解它的思想方法，熟悉它的实际应用，而不至于只是形式地去“理解”它的定义，机械地去“掌握”它的方法呢？重要的是如何引导学生从数列极限的“描述性”定义向“精确性”定义过渡，从一般的叙述语言向“ε-N”语言转化。这一教学重点和难点必须从教和学两个方面突破。建构主义提倡在教师指导下，以学习者为中心的学习。也就是说，既强调学习者的认知主体作用，又不忽视教师的指导作用，两者相得益彰、和谐发展，为突破难点提供了有力的支撑。

建构主义理论把“情景”、“协作”、“会话”和“意义建构”作为学习环境的四大要素。为突破数列极限的教学难点，笔者通过多媒体课件演示模型精心设计了“问题环境”，再通过师生之间的“会话”、“协作”，逐步完成学生的“意义建构”。

一、以模型驱动思维，引导学生认识“无限”

教学中先从《庄子。天下篇》中“一尺之棰，日取其半，万世不竭”中，使学生初步认识“无限”。然后利用多媒体课件演示“无限”的数学模型，引导学生辩证的认识“无限”。

模型（课件演示）我国古代（公元3世纪）数学家刘徽的“割圆术”：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”意思是：圆内接正多边形的边数越多，正多边形的周长与圆的周长误差就越少，正多边形的边数再增加，一直到正多边形的边不能再分割时，则正多边形的周长就是圆的周长。

首先，这句话的要点在于“割之又割”，没有“割之又割”，就没有“以至于不可割”，也就没有了“合体”之说。因而“割之又割”是一种变化过程，是一种没完没了的变化过程，即“无限”变化过程，所以“无限”实质上是一种永不停止的变化过程。

其次，“割之又割，以至于不可割，则与圆周合体而无所失矣。”这是思维上的一种认识，是思维上的一种飞跃——辩证思维。“不可割”是思维上的不可割，是思维上的一个“终结”，不是实际上的，实际上永远达不到“不可割”。有了这种思维认识就顺理成章地有了“合体”之说。永不停止的“无限”变化过程，有时也有一个“终结”，而这个“终结”不是实质上的“终结”，而是一种变化趋势。

二、以具体数列深化思维，引导学生形成“描述性定义”

1.多媒体演示以下数列，描绘数列的图象

（多媒体课件动感表示）将这四个数列直观表示在直角坐标中，描绘出每个数列的图形(略)。

2.通过观察引出“描述性”定义

让学生观察分析数列的图形后不难发现：当项数n无限增大时，数列（1）的一般项无限接近于常数0；数列（2）的一般项无限接近于常数1；数列（3）的一般项无限接近于常数1；而数列（4）的一般项xn

在1与-1之间摆动，不趋向于某一个确定的常数。

教师：当项数无限增大时，如果数列的一般项能无限接近于一个常数，则称这个常数为数列的极限。这就是数列极限的“描述性”定义（同时板书此定义）。

三、“ε-N”精确化定义的形成和概括过程

1.在“会话”、“协作”中让学生主动构建知识

用《几何画板》考察数列（2）的图像，学生可亲自参与，用鼠标拖动图形中标注的拖动点，观察数列的一般项随n变化的过程，反复实践，反复体验何谓“趋向于”。在此基础上，老师与学生进行“会话”、“协作”共同再认识“描述性”定义，为“描述性”定义向“精确化”定义过渡作准备。

2.在交流协作中完成“ε-N”精确化定义

如何用准确、精炼的数学语言来刻划“n无限增大”、“xn无限接近”呢？经过学生间的交流协作，在若干次的修改、补充、完善后，形成如下的表述：

极限的“ε-N”定义：∀ε＞0无论它多么小，∃正整数N，当n＞N时的一切项xn，恒有则称常数a是数列{xn}的极限，记作

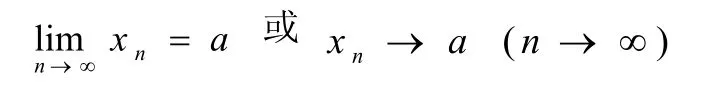
四、“ε-N”精确化定义的进一步分析

至此，教师还须对“ε-N”定义中的语言作进一步的解释，要指出：

①ε与N的逻辑关系是先有ε后有N，关系不容颠倒。定义中的N是变化过程的界限，N由相应的ε来确定，ε越小，N越大，有时也记为N(ε)，但并不意味着N由ε唯一确定。因为ε取定后，N的选取并不唯一（老师可用上面的例子再作解释）。

②ε是任意给定的正数，它具有两重性。一是它的任意性，因此它不是一个固定的常数，以保证要多么小就有多么小，它刻划xn无限接近于a的程度；二是它的相对固定性，ε一经取定，就相对固定了下来，以便根据它去求出N，但ε的本质是一个常量。

④定义中并不是、也不需要数列{xn}的所有项xn均满足＜ε，而是当n增大到一定程度时，比如n＞ N以后的所有项满足＜ε就可以了，至于N之前的有限个项是否满足＜ε并不影响常数a是数列{xn}的极限。

五、从理性认识又回到感性认识，对定义作几何解释

至此，同学们对数列的极限已经有了一个明确的并且直观的认识。

六、用极限的“ε-N”定义来证明数列的极限

需要说明的是：对于给定的ε，能够说明N确实存在即可，没有必要求出最小的N是什么。因此，为了求解方便，我们总是把不等式作适当的放大，利用放大之后的式子小于ε，解不等式得到N。

还可以再举几个证明极限的例子，本次课就可以结束了。

[1] 张奠宙，张荫南. 新概念用问题驱动的数学教学[J]. 高等数学教育，2004，3.

[2] 徐利治. 数学方法论选讲[M]. 华中工学院出版社，1998.

[3] [ 瑞士]皮亚杰. 发生认识论原理[M]. 商务印书馆，1995.

[4] 郭运瑞. MM教育方式与数学创新教育的教学原则[J]. 职业技术教育，2001，3.

[5] 同济大学. 高等数学[M]. 高等教育出版社，2003.

From the Icy Beauty of “ε-Ν” Limit Method to Emotional Thinking

DONG Fang-liang，JIN Wei-min

Mathematics is dual, “Passionate thinking” and “icy cold beauty”. Mathematics education should convert the academic form on the textbook to an easier way for the student. The precision of mathematics presents a kind of “icy cold beauty”. But the discoveries and comprehension of mathematics reflect “ passionate thinking”. This paper will take the numerical sequence limit as an example, and tentatively talk about the duality of mathematics.

Passionate thinking; numerical sequence limit; construction principle; mathematic thinking method

O171

A

1008-7427（2010）06-0159-02

2010-03-23

河南省教育厅自然科学研究项目，项目编号：2007110019。作者董方亮系鹤壁职业技术学院讲师。