利用 Jacobi椭圆函数展开法求解特殊类型的方程
沈水金
(1.上海大学 理学院,上海 200444;2.绍兴文理学院 数学系,浙江绍兴 312000)
利用 Jacobi椭圆函数展开法求解特殊类型的方程
沈水金1,2
(1.上海大学 理学院,上海 200444;2.绍兴文理学院 数学系,浙江绍兴 312000)
利用未知函数的变换,将非线性演化方程转换为以新未知函数及其偏导数为变元的多项式型的非线性偏微分方程,再应用 Jacobi椭圆函数展开法,求解 sine-Gordon方程和 Dodd-Bullough-M ikhailov方程的精确周期解,所得的周期解包含孤波解.该方法同样适用于求解其他非线性演化方程.
非线性演化方程;Jacobi椭圆函数;精确周期解;孤波解
Abstract:By transformation of a dependent variable,a nonlinear evolution equation (NLEE) is converted into a nonlinear partial differential equation(NPDE)with apolynomial type of a new dependent variable and its partial derivatives.A Jacobi ellip tic function expansion method is p roposed to construct the exact periodic solutions of several nonlinear equations—sine-Gordon equation and Dodd-Bullough-Mikhailov equation.Periodic solutions obtained with this method include the solitary solutions and the shock wave solutions.Themethod can also be app lied to other nonlinear evolution equations.
Key words:nonlinear evolution equation;Jacobi ellip tic function;exact periodic solution;solitary solution
自 1834年 Russell第一次发现孤波现象、1967年 Gardner等利用反散射方法求得 KdV方程的孤波解之后,寻找非线性演化方程[1-2](nonlinear evolution equation,NLEE)的显示解成为非线性领域中的热门课题之一,尤其是寻找高维非线性演化方程的孤波解和类孤波解.为了获取非线性演化方程更多的精确周期解,人们提出了许多种方法,如 Hirota双线性算子、Bäcklund变换、Darboux变换、Painlevé展开法等.近年来,刘适达等[3-4]提出的 Jacobi椭圆函数展开法在求解非线性演化方程中得到了广泛应用.该方法不仅能求得非线性演化方程 (组)的精确周期解 (其中包含孤波解),并且通过对 Jacobi椭圆函数展开形式进行适当修改[5-6],得到更多的精确周期解.但无论如何,Jacobi椭圆函数展开法都需要通过对 Jacobi椭圆函数次数的平衡[7]来求得 n值.因此,对于方程中出现的类似 sin u,eu等无法直接通过次数的平衡来求 n值的特殊式子,必须要对其进行等价替换,从而满足次数平衡的要求.本工作主要通过用未知函数的等价替换,将非线性演化方程替换为,以新未知函数及其偏导数为变元的多项式型[8]的非线性偏微分方程,再通过 Jacobi椭圆函数展开法求解精确周期解.
1 Jacobi椭圆函数展开法
考虑非线性波动方程

其行波解为

式中,k和 c分别为波数和波速.
将 u(ξ)展开为 Jacobi椭圆正弦函数 snξ的级数,有

其最高阶数为 O(u(ξ))=n.因为

式中,cnξ和 dnξ分别为 Jacobi椭圆余弦函数和第三种 Jacobi椭圆函数,且具有如下性质:

类似地,可以认为

在式 (3)中选择 n,使得非线性方程 (1)中的非线性项和最高阶导数项平衡,从而求得方程的精确周期解.特别地,当 m → 1时,snξ=tanhξ,式 (3)就转化为
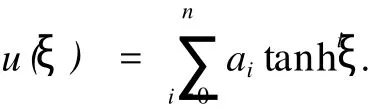
所以,Jacobi椭圆函数法包含了双曲正切函数展开法.
2 特殊方程的等价替换
Jacobi椭圆函数展开法需要通过对式 (1)中的非线性项和最高阶导数项平衡来求式 (3)中的 n值.对于个别特殊类型方程中存在的类似 sin u,eu等的式子,无法直接通过平衡求解,因此,有必要对类似 sin u,eu等的式子进行等价替换.不妨作未知函数的替换:

显然,若 v(x,t)是方程 (10)的解,则替换式 (7)所得到的 u(x,t)必定是方程 (9)的解,因此,方程 (9)与方程 (10)等价.
3 求解方程
3.1 sine-Gordon方程的精确周期解
由未知函数的替换公式 v=eiu,得

则方程 (9)与方程 (10)等价,因此,只需求方程 (10)的精确周期解.令
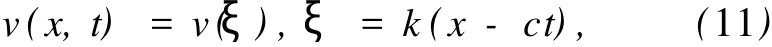
将式 (11)代入方程 (10),得

通过对最高阶导数项和非线性项平衡,得 n=2,因此,可以假设方程 (12)有如下形式的解:


将式 (13)~(15)代入式 (12),得

通过吴消元法求得此方程组的解,情况如下.
情况1:

此时,方程 (12)的解为



这就是 sine-Gordon方程的双曲正切函数解,利用此解能求得该方程的孤波解.
情况2:
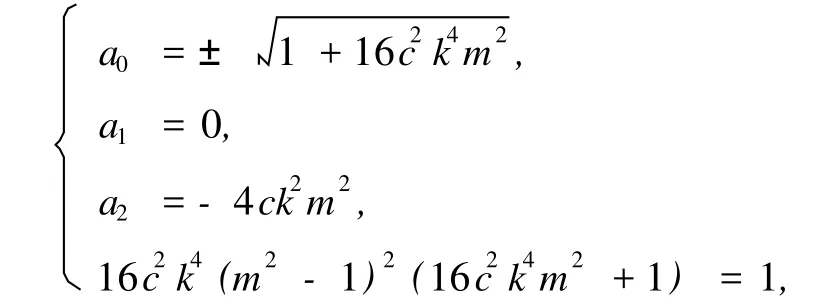
此时,方程 (12)的解为


3.2 Dodd-Bullough-M ikha ilov方程的精确周期解



将式 (11)代入方程 (19),得
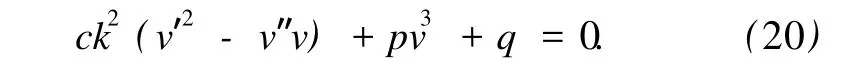
通过次数平衡,求得 n=2,因此,可以假设方程 (20)有如下形式的解:
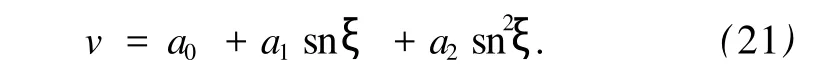
将式 (21)代入方程(20),令所得方程的各项系数为0,得
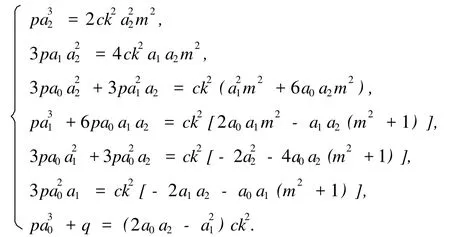
通过吴消元法,求得该方程组的解为



4 结 束 语
本工作利用 Jacobi椭圆函数展开法求解特殊类型的方程,关键在于利用未知函数的等价替换,将非线性演化方程转变成为多项式形式的非线性偏微分方程.不同类型的未知函数需要不同类型的等价替换公式,从而得到非线性演化方程的精确周期解.最后指出,对于各种替换得到的等价方程,可以利用不同的求解方式来求得精确周期解.
致谢:衷心感谢导师夏铁成教授的指导和帮助.
[1] 范恩贵.可积系统与计算机代数 [M].北京:科学出版社,2004:14-24.
[2] YANG L,ZHU Z G,WANG Y H.Exact solutions of nonlinear equation[J].Physics Letters A,1999,260(1/2):77-84.
[3] 刘式适,傅遵涛,刘适达,等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用 [J].物理学报,2001,50(11):2068-2073.
[4] L IU SK,FU Z T,L IU SD,et al.Jacobi elliptic function expansion method and periodic wave solution of nonlinear wave equations[J].Physics Letters A,2001,289(1/2):69-74.
[5] ZHOU Y B,WANG M L,WANG Y M.Periodic wave solutions to a coupled KdV equations with variable coefficients[J].Physics Letters A,2007,308(1):31-36.
[6] 张善卿,李志斌.Jacobi椭圆函数展开法的新应用 [J].物理学报,2003,52(5):1066-1069.
[7] FAN E G. Extand tanh-function method and its app lications to nonlinear equations[J].Physics Letters A,2000,277(4/5):212-218.
[8] WU W T. Polynomial equation-solving and its application,algorithms and computation[M].Berlin:Sp ringer-Verlag,1994.
(编辑:孟庆勋)
Applications of Jacobi Elliptic Function Expansion M ethod to Several Special Nonlinear Equations
SHEN Shui-jin1,2
(1.College of Sciences,Shanghai University,Shanghai200444,China;2.Department of Mathematics,Shaoxing University,Shaoxing 312000,Zhejiang,China)
O 175.2
A
1007-2861(2010)04-0383-04
10.3969/j.issn.1007-2861.2010.04.011
2009-01-12
沈水金 (1980~),男,硕士,研究方向为计算数学.E-mail:zjssj595@yahoo.com.cn

