一种改进的全阵空间平滑技术*

(空军工程大学 导弹学院，陕西 三原 713800)

1 引 言

近二十多年来，信号波达方向(DOA)估计研究受到广泛重视，在雷达、声纳、通信中尤为重要。基于信号子空间的MUSIC(Multiple Signal Classification)算法和ESPRIT算法是目前比较好的DOA估计算法。MUSIC算法利用阵列协方差矩阵R的噪声子空间和信号子空间的正交性进行DOA估计，对于非相干或相关程度较小的空间信源具有良好的分辨性能。然而，当信号相干时，信号源的协方差矩阵就会变成奇异阵，信号子空间将向噪声子空间扩散，这时，MUSIC算法的分辨性能就会恶化甚至失效。

空间平滑最初是由Evans[1]提出来的，后来Shan[2]进行了完善，其基本思想是把主阵划分为若干相重叠的子阵列，然后对子阵的协方差矩阵求平均(各子阵列的向量以各自的第一个阵元为基准，两相干信号的相位差由于波达方向不同，使空间平滑产生随机相位调制，因而可以对引起秩亏缺的信号解相关)。利用这种方法，我们可以得到满秩的协方差矩阵，然后用MUSIC算法。在这些传统的方法中，能处理的相干源最大范围是2N/3(N为阵列的阵元数)[3-4]，可检测相干源数目与子阵孔径大小成为矛盾，随后提出一些增强平滑技术方法[5]和利用互相关矩阵信息的前后向平滑[6]等在一定程度上增强了对空间相干源的解相关能力，但计算量比较大。Nizar在文献[7]中提出C-SPRIT进行非圆信号如二进制相位键控(BPSK)和M进制幅度键控(MASK)DOA估计，随后又利用C-SPRIT思想，提出CMUSIC方法[8]来解决非圆相干信号DOA估计，利用N个阵元估计N-1个非圆相干信号DOA，但也只是使信号源有相干变为相关，并没有彻底解相关。利用本文的算法，能处理的最大相干源数目为N-1(为全阵的自由度)，而且在处理SNR较低或波达角相邻近时的相干源也有效。

2 算法分析

假设一个N元等距线阵(ULA),假定P个窄带平面信号源波达方向角分别为θ1,θ2,…,θp,那么，N个阵元接收的信号矢量可以写为

(1)

式中，sk(t)代表第k个信号，其源波达角为θk；a(θk)表示N元阵的导向矢量；n(t)是N×1的均值为零、方差为σ2的加性高斯白噪声。阵列导向矢量可以写成

(2)

式中，上标T代表转置，

(3)

式中，λ是波长，d是相邻阵元的间距，N×P的阵列响应矩阵和P×1的信号矢量可以写为

A(θ)=(a(θ1),a(θ2),…,a(θP))

(4)

和

S(t)=(s1(t),s2(t),…,sP(t))T

(5)

接收到的信号矢量可以写为

X(t)=A(θ)S(t)+n(t)

(6)

图1 阵元

本文方法用N元子阵，每个子阵的阵元数等于全阵列N，由图1，子阵1写为

Y1(t)=A(θ)S(t)+n1(t)

(7)

式中，

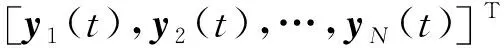
(8)

(9)

(10)

(11)

A(θ)Φ*S(t)+n2(t)

(12)

式中，

(13)

(14)

子阵3可以写为

A(θ)(Φ*)2S(t)+n3(t)

(15)

A(θ)(Φ*)N-1S(t)+nN(t)

(16)

式中，

(17)

(18)

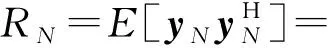
AH(θ)+σ2I

(19)

式中，上标H表示对矩阵进行共轭转置操作，RS=E[s(t)s(t)H]是P×P的信号协方差矩阵，如果存在相干信号，Rs的秩小于P，那么我们可以用R1,R2,…,RN的平均得到满秩的矩阵。

(20)

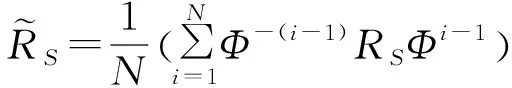
考虑一个8元ULA阵，传统的方法让每个子阵的阵元数为6，我们可以发现子阵4和子阵5在最后平均得到协方差矩阵时并没有被用到，并且其它子阵的阵元数也少于8(全阵的阵元数)。很明显，本文的方法比传统方法利用了更多的资源。

图2 本文方法与前后向平滑方法在子阵阵元数上的比较(在子阵6中y1等于

3 仿真与分析

我们用几个仿真例子来证明本文所提方法的有效性，统一使用8元阵，快拍数为500。

仿真1，考虑3个等能量的相干源，DOA分别为θ1=-40°、θ2=-20°、θ3=0°，信噪比(SNR)为-10 dB。仿真结果如图3所示。其中，图3(a)中很难精确地在-40°～-20°和0°观察到峰值，多次实验结果的DOA峰值都不一样。然而，在图3(b)中我们可以清楚地看到3个尖峰，并且DOA估计比较准确，多次实验的峰值位置都基本相同。这证明了本文方法在信噪比较低情况下的有效性。

(a)前后向平滑方法

(b)本文方法图3 仿真结果

仿真2,对两个等功率相干源，信噪比为5 dB,其波达角是θ1=10°、θ2=15°，分别作50次蒙特卡罗仿真。子阵阵元数是7，为前两种方法条件下两个相干源下最多的阵元数。比较前后向平滑以及加权前后向平滑，两种方法中峰值的位置都偏离了真实值。如图4所示，因本文所提出的方法每个子阵阵元数等于8，而其它的方法所涉及子阵阵元数小于8，所以此方法更为精确。从图4中可以看出，本文所提出的方法估计的DOA峰值位置在真实值，而其它两种方法则偏离较大。

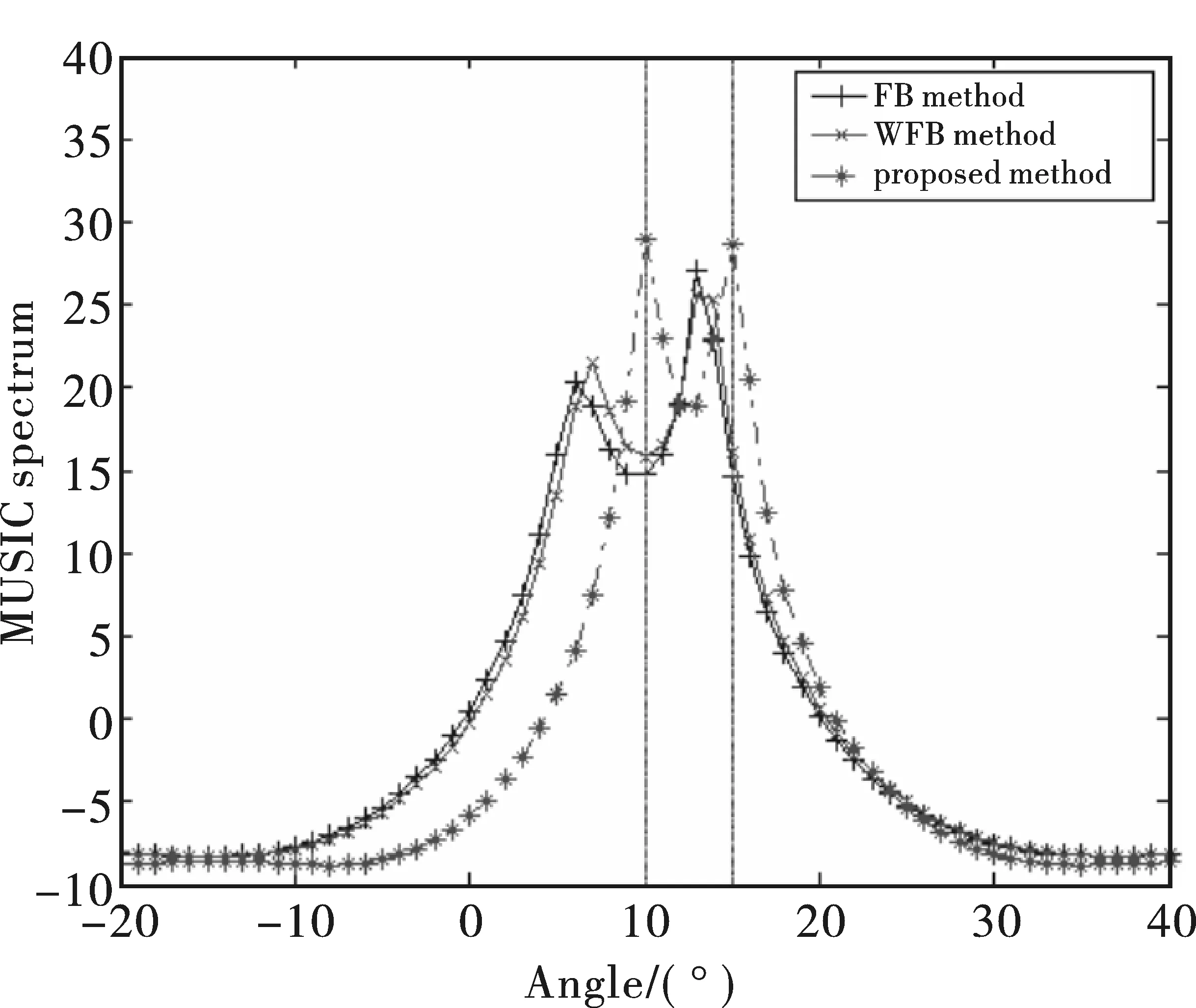
图4 波达角分别为10°、15°,信噪比为5 dB时仿真比较图

在下面的仿真中，分别对波达角为10°、15°，信噪比是10 dB的等功率相干源求均方根误差，在不同的相关系数条件下进行仿真，结果如图5所示，可以看出本文方法均方根误差比前后向平滑以及加权前后向平滑均方根误差都小。同样，在不同信噪比的情况下，如图6所示，结果均体现该方法的优越性。其中图5和6比较的是不同DOA的估计均方根误差的结果。从图中可以看出，本文方法估计信号DOA的方差均要比前后向平滑、加权前后向平滑方法的要低。

仿真3，用本文的方法，我们可以估计N-1个相干源，N为阵元数目，但传统方法无法做到，图7验证了本文方法的可行性。相干源数目为7，波达方向角(DOA)为-60°、-40°、-20°、0°、20°、40°、60°,信噪比为0 dB。

传统的方法由于采用前后向平滑技术，使得阵列孔径有所损失，估计信号DOA数目大大减少。而本文方法不采用前后向平滑技术，利用子阵之间的虚拟平滑，达到无孔径损失的效果，使得估计的DOA数目达到最大，为阵列的最大孔径(极限值)。

(a)波达角为10°

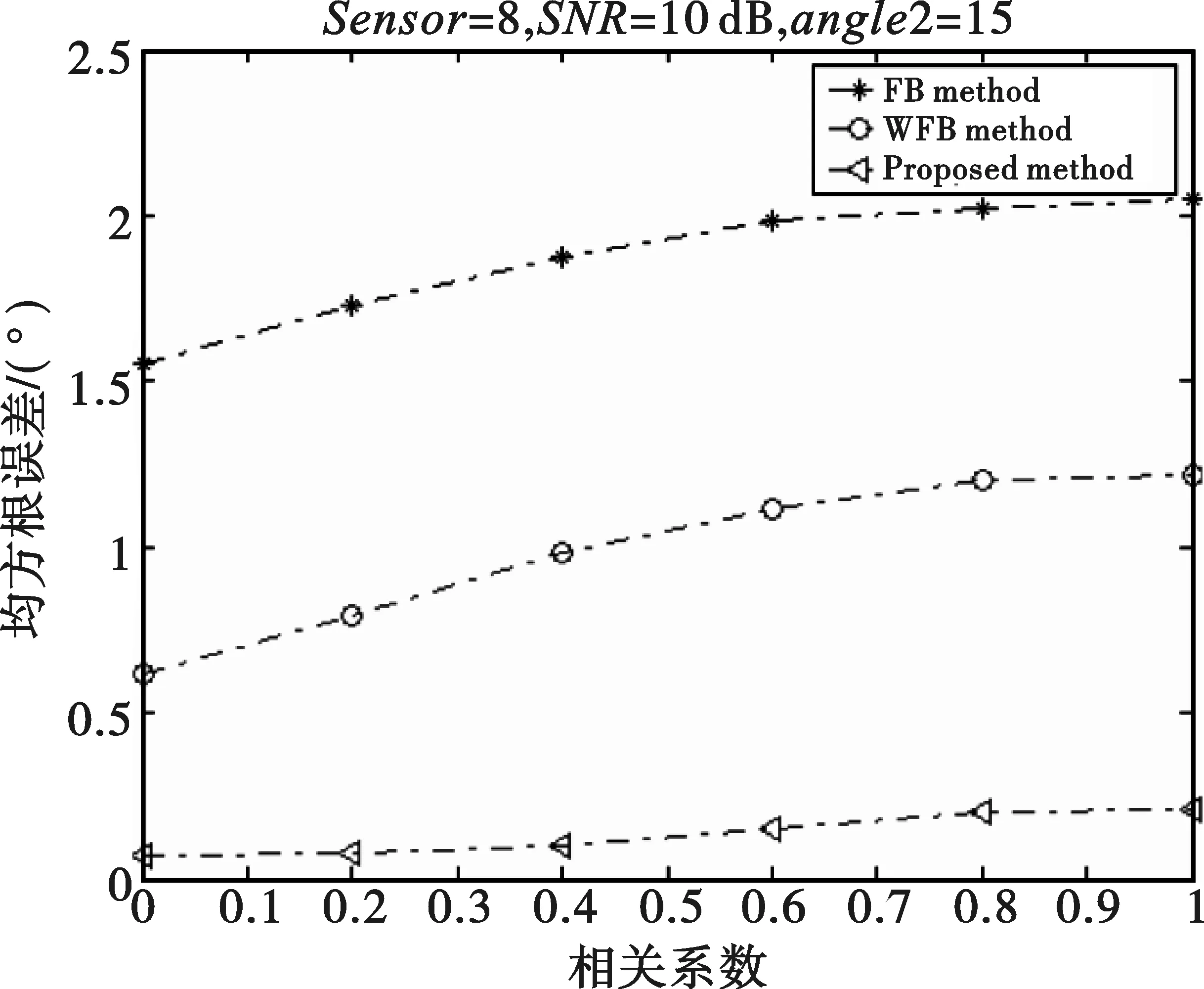
(b)波达角为15°图5 SNR=10 dB时不同相关系数均方根误差

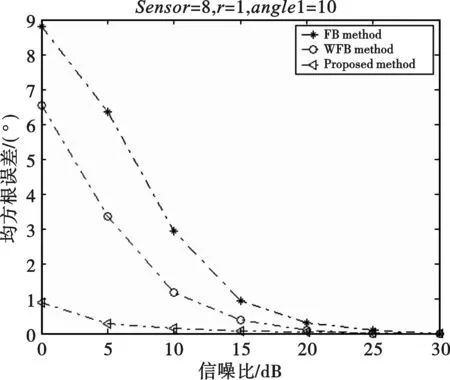
(a)波达角为10°

(b)波达角为15°图6 不同信噪比下均方根误差

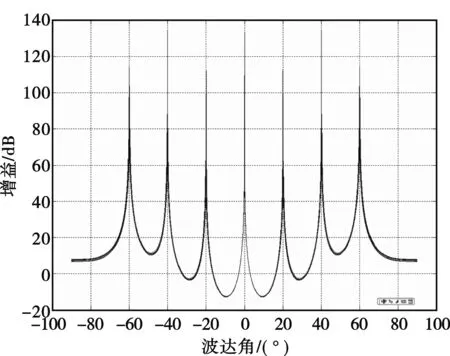
图7 用本文方法10次试验得到的空间谱估计(阵元数为8，相干源为7，信噪比为0 dB)

4 结 论

本文提出了一种可以充分利用全阵进行相干源估计的方法。该方法相对于传统方法的优越性是显而易见的，尤其当相干源数目较大或未知时，本文方法可以估计的相干源数等于全阵时的最大数，是全阵估计信源的上限。并且，由于本文方法没有孔径损失，在同样DOA数目的估计情况下，单个信号DOA估计精度会得到大大提高，尤其是低信噪比的情况下，其优越性更加明显。

参考文献：

[1] Evans J E, Johnson J R, Sun D F.Application of advanced signal processing techniques to angle of arrival estimation in ATC navigation and surveillance system[R]//Technical Roport 582.Lexington,MA:M I T Lincoln Lab,1982.

[2] Shan T J, Han M Wax, Kailath T.On spatial Smoothing for Direction-of-Arrival Estimation of Coherent Signals[J].IEEE Transactions on Acoustic, Speech and Signal Processing, 1985,ASSP-33(4):806-811.

[3] Yoram Bresler, Albert Macovski.On the number of signals resolvable by a uniform linear array[J]. IEEE Transaction on Acoustics, Speech and Signal Processing, 1986,ASSP-34(6):1361-1375.

[4] Ronald T Williams, Surendra Prasad, Mahalanabis A K,et al. An improved spatial smoothing technique for bearing estimation in a multipath environment[J].IEEE Transactions on Acoustics, Speech and Signal Processing,1988,36(4):425-432.

[5] Choi Y H.Subspace-based Coherent Source Localisation with Forward/Backward Covariance Matrices[J].IEE Proceedings Radar Sonar Navigation,2002,149 (3):145-151.

[6] 王布宏, 王永良, 陈辉. 相干信源波达方向估计的加权空间平滑算法[J]. 通信学报,2003,24(4):31-40.

WANG Bu-hong,WANG Yong-liang, CHEN Hui.Weighted Spatial smoothing for Direction-of-Arrival Estimation of Coherent Signals[J]. Journal on Communications,2003,24(4):31-40. (in Chinese)

[7] Nizar Tayem,Kwon H M.Conjugate ESPRIT (C-SPRIT) [J].IEEE Transactions on Antennas and Propagation,2004,52(10):2618-2624.

[8] Amjad Salameh,Nizar Tayem. Conjugate MUSIC for non-circular sources[C]//Proceedings of 2006 IEEE International Conference on Acoustics, Speech and Signal Processing. Toulouse:IEEE,2006:877-880.