基于非线性最小二乘的三星座时差定位综合算法*

李 悦，2，柳 征3，伍渝江

(1.兰州大学 数学与统计学院，兰州 730000；2.解放军61541部队，北京 100094；3.国防科技大学 电子科学与工程学院，长沙 410073)

1 引 言

三星座时差定位系统[1]通过三颗星测量同一脉冲的TOA(Time of Arrival)，形成两路时差曲面，加上地球面的约束，实现对地面辐射源的定位。但在实际中，被侦察辐射源往往在卫星过顶时段关机，规避侦察，达到反侦察的目的。这种情况下，三星座定位系统只能在过顶前、后的一小段时间捕获有关目标的少量数据，这种数据被称为弱观测数据，并将此类目标源所处的区域称为弱观测区。现有三星座定位方法多采用牛顿迭代或解析法[2]，利用两路时差数据和地球模型进行定位解算，当过顶时段无法获得有效数据时，现有方法不能充分利用弱观测数据，对弱观测区目标定位精度较差，并且受目标高程误差影响较大，当目标没有先验高程信息支持时，定位精度不理想[2]。

针对上述问题，本文重点研究弱观测数据定位综合处理问题，提出一种基于非线性最小二乘(NLS)的时差定位综合算法。

2 三星座时差定位综合算法

如图1所示，三星座仅在过顶前和过顶后的实线区域对目标辐射源进行了有效观测，而过顶时的虚线区域辐射源关机规避。根据文献[2]的定位误差分析可知，采用牛顿迭代法定位在过顶时段定位效果较好，过顶前、后定位效果相对较差。因为文献[2]的定位方程采用了地球模型作为约束，所以高程假设在很大程度上影响了定位精度。时差定位综合算法将过顶前的数据同过顶后的数据配对综合处理，在一次定位运算中通过同时运用过顶前、后的两组观测数据，提高定位精度，同时定位方程不依赖地球模型作为约束，对近地目标定位精度稳定，不受高程影响。

图1 弱观测数据定位示意图

假设目标真实位置为X(x,y,z)，三星座在过顶前和过顶后的观测位置分别为

(1)

(2)

对目标进行观测可得到4个有效时差值[3-5]，据此可进行三维定位[1]。假设三星座在过顶前位置得到的两组时差测量值为t1、t2，在过顶后位置观测得到的两组时差测量值为t3、t4。在没有测量误差时，ti与真实时差相等，当引入误差后：

cti=fi(X)+ni,i=1,2,3,4

(3)

式中，c为电磁波传播速度，ni为误差项，为方便将cti记为ri：

ri=fi(X)+ni,i=1,2,3,4

(4)

方程组可以重写为

(5)

式中 ‖·‖2表示2-范数。可以将方程(4)写成一个向量等式:

r=f(X)+n

(6)

测量误差n为多元随机变量，其协方差矩阵记为4×4的正定矩阵N：

N=E[(n-E(n))(n-E(n))T]

(7)

因为N为对称的正定矩阵，所以N有逆。在三星座定位系统中，我们认为真实位置X为未知的非随机变量，测量误差n为零均值高斯噪声。由文献[6-8]，r关于X的条件密度函数为

则式(8)的极大似然估计为使P值最大的X，令

Q(X)=[r-f(X)]TN-1[r-f(X)]

(9)

可知式(8)的极大似然估计等价为Q(X)最小。

事实上,这种最小化Q(X)的估计方法对非高斯噪声也是合理的，因为N-1在方程(9)中仅被视为权系数矩阵。

距离方程f(X)为非线性方程组，将f(X)线性化，在迭代点X0附近泰勒展开，保留前两项有:

f(X)=f(X0)+f′(X0)(X-X0)

(10)

(11)

将式(10)代入式(9)得:

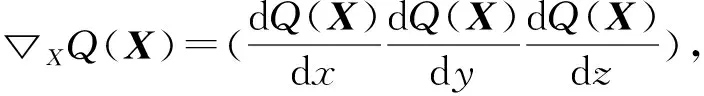
迭代格式为

3 误差分析

本节给出时差定位综合算法同文献[2]中牛顿迭代法的误差理论分析及GDOP分布。

3.1 时差定位综合算法误差分析

式(13)经过简单的变换可得：

由式(15)可以看出，估计误差受到线性化和噪声的影响，假设线性化误差为零，则对真值的估计是无偏的，且误差为

(16)

令

(17)

则式(16)可以写成:

(18)

定位误差协方差矩阵为

(20)

定位误差的GDOP分布[9]为

(21)

3.2 牛顿法误差分析

由文献[2]可知，牛顿法迭代格式为

Xk+1=Xk-[g′(Xk)]-1g(Xk)

(22)

式中，g(X)为定位方程组，处理方法同3.1，得:

(23)

误差协方差矩阵为

定位误差的GDOP分布为

(25)

4 仿真结果和分析

本节给出两组仿真结果：4.1节将时差定位综合算法与文献[2]提出的牛顿迭代法的定位误差GDOP图进行对比分析，来验证时差定位综合算法对弱观测数据的处理能力；4.2节中给出了两个相差3 km高程的真实定位点，通过比对分析，给出高程对两种算法定位精度的影响。比对指标主要考虑定位误差。鉴于三星时差定位的应用背景是对全球可能辐射源的定位，因此应当采用全球平均误差较小的地心大地坐标下的地球椭球。目前,以GPS为代表的应用中用的都是WGS-84坐标系[10]，因此，本文仿真中所用地球椭球都采用WGS-84坐标系的地球椭球，方程为

(26)

式中a=6 378 137 m,e2=0.006 694 379 990 13。卫星的高度约为1 000 km，星间距约为110 km，成三角形分布，过顶前后观测时间间隔为700 s。

过顶前卫星真实位置为A1(-2.2552×106,5.7649×106,4.3409×106)m，B1(-2.1702×106,5.7321×106,4.4235×106)m，C1(-2.2578×106,5.706×106,4.4286×106)m。

过顶后卫星真实位置为A2(-4.6821×106,5.9947×106,2.5667×105)m，B2(-4.6411×106,6.0212×106,3.5363×105)m，C2(-4.7180×106,5.9603×106,3.8311×105)m。

在式(14)、(22)的迭代过程中，初始迭代点的选择会影响解的精度[11]，我们不进行讨论。在仿真过程中使用卫星A观测时刻星下点作为初始迭代点，在实际应用中可以采用文献[2]的解析解作为时差定位综合算法的初始迭代点。

4.1 定位误差GDOP分布图

本小节给出3种定位方法在不同误差条件下的定位误差GDOP分布。其中定位方法1为时差定位综合算法；定位方法2为牛顿法，在图3中我们将牛顿法过顶前后的两次定位误差GDOP分布图合在一起给出；定位方法3是将牛顿法在过顶前、后的两次定位结果的算术平均作为定位结果。3种方法的误差GDOP图如图2～4所示。

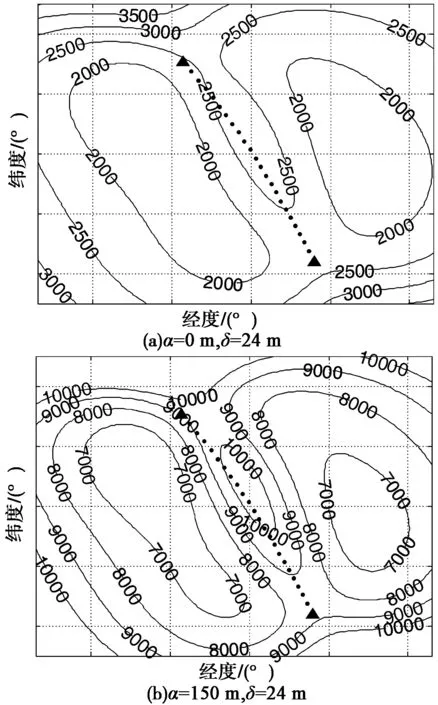
图2 方法1定位误差GDOP分布图

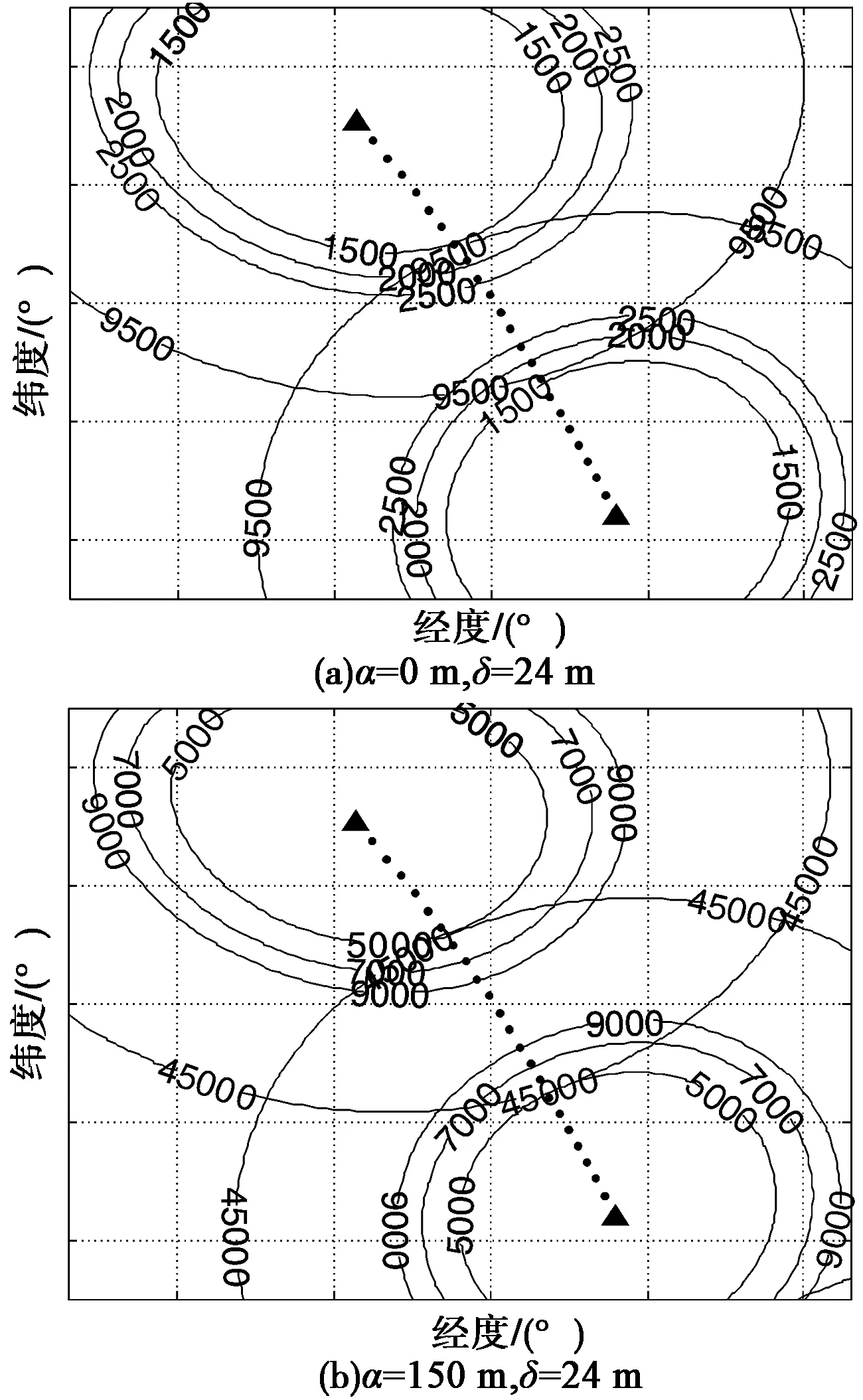
图3 方法2定位误差GDOP分布图

图4 方法3定位误差GDOP分布图

图2～4给出了3种定位方法对零高程目标在不同的测距误差和星址测量误差条件下定位产生的误差GDOP分布，图中黑色实心三角表示三星座在观测位置的地面投影，三角间的连接虚线为卫星航迹的地面投影。弱观测区域为图中卫星航迹的中垂线附近。当α=0 m、δ=24 m，方法1对弱观测数据的定位误差主要分布在2 000 m以内，少量分布在2 000～2 500 m；方法2定位误差主要分布在2 500～9 500 m；方法3产生的误差为2 500～3 000 m。当α=150 m、δ=24 m时，方法1对弱观测数据的定位误差主要分布在7 000～9 000 m，方法2定位误差主要分布在9 000～45 000 m，方法3产生的误差为8 000～12 000 m。可以看出，在两种误差条件下，方法1对弱观测区目标的定位精度要高于方法2和方法3。

为了更清楚地表现3种方法的各自定位优势，我们给出相对误差GDOP图，即将两种不同方法的误差值做比值，则GDOP图的1等高线将定位好坏明显区分。如图5所示，我们仅就α=150 m、δ=24 m一组误差条件做相对GDOP对比。

图5 相对定位误差GDOP分布图

图5(a)是方法3与方法2的相对GDOP图，小于等高线1的区域表示方法3定位精度高于方法2，可以看出，方法3对弱观测区目标定位要好于方法2。图5(b)是方法1与方法2的相对GDOP图，可以看出，方法1对弱观测区目标定位要好于方法2。图5(c)是方法1与方法3的相对GDOP图，表明方法1对弱观测区定位好于方法3。通过对相对误差GDOP图的分析，显然，方法1对弱观测区目标的定位精度是最高的。

4.2 不同高程目标定位实验

运用4.1节中的3种定位方法对两个有高程差的弱观测区目标在不同误差条件下定位，为方便理解，目标改用经纬高坐标，WGS-84坐标系的坐标转换参照文献[2]。目标A(128.8,25.492,0)、B(128.8,25.492,3000)，这两点仅在高程有差异。定位误差结果如表1所示。其中方法2有两组结果，分别为过顶前、后两次定位的误差。

表1 定位误差对比Table 1 Comparison of position error m

通过对表1数据纵向比较，显然方法1对弱观测数据在两种误差条件下定位效果都要好于方法2和方法3。通过横向数据比较，发现方法1定位精度并不受高程影响，在0高程和3 km高程上，定位误差基本保持稳定。方法2和方法3的定位误差都随高程增加而增加，这是由于定位方程依赖地球模型方程，高程对方法2和方法3定位误差的影响文献[2]中有详细的讨论。当观测目标可以确定高程时，例如对海面舰船目标的观测，认为目标零高程，可以将方法1的结果在高程面做投影得到结果，这样可以提高定位精度。

5 结 论

基于WGS-84模型的时差定位方法在电子战、导航等领域有较为广泛的应用。实际应用中，因为卫星轨道相对固定，所以目标往往对卫星侦察进行规避，导致卫星在过顶时段不能获得有效数据。因此，研究弱观测区的时差定位方法应该是具有实际意义的。

本文以处理三星座弱观测区数据为背景，提出了一种基于NLS的时差定位综合方法，分析了该方法对目标定位的原理，并对其定位误差进行了理论推导与数值分析。通过与其它方法的比较表明，在弱观测区该方法能获得更优的定位结果，同时该方法不受目标高程影响，对近地目标能够提供稳定的定位结果。

参考文献：

[1] 孙仲康，周一宇，何黎星. 单多基地有源无源定位技术[M].北京:国防工业出版社，1996.

SUN Zhong-kang , ZHOU Yi-yu , HE Li-xing. Sigle/Mulit-Bulti-Base Active and Passive Location Technology[M].Beijing: The National Defense Industry Press,1996. (in Chinese)

[2] 钟丹星. 低轨三星星座测时差定位方法若干问题研究[D].长沙:国防科学技术大学，2002.

ZHONG Dan-xing. Research on some technology problems of Low-Earth-Orbit 3-satellites location system using TDOA measurements[D]. Changsha: National University of Defense Technology, 2002. ( in Chinese)

[3] Schmidt R O. A new approach to geometry of range difference location[J]. IEEE Transactions on Aerospace Electronic Systems,1972, 8(4): 821-835.

[4] Hahn W R,Tretter S A.Optimum processing for delay-vectorestimation in passive signal arrays[J]. IEEE Transactions on Information Theory, 1973, 19(9): 608-614.

[5] Spirito M A.On the accuracy of cellular mobile station location estimation[J]. IEEE Transactions on Vehicle Technology,2001, 50(5): 674-685.

[6] Mensin C,Plass S.Positioning algorithms for cellular networks using TDOA[C]//Proceedings of Internationnl Conferen ce Acoustics Speech Signal Processing (ICASSP).Toulouse,France:[s.n.],2006: 513-516.

[7] So H C,Chan Y T,Chan F K W.Closed-form formulae foroptimum time-difference-of-arrival based localization[J]. IEEE Transactions on Signal Process, 2008, 56(8): 2614-2620.

[8] Torrieri D J.Statistical theory of passive location systems[J]. IEEE Transactions on Aerospace Electronic System,1984, 20(2): 183-197.

[9] Levanon N. Lowest GDO Pin 2-D scenarios[J]. IEE Proceedings of Radar Sonar Navigation, 2000, 147(3): 149-155.

[10] 郗晓宁,王威,高玉东.近地航天器轨道基础[M].长沙:国防科技大学出版社,2003.

XI Xiao-ning, WANG Wei,GAO Yu-dong. Fundamentals of Near-earth Spacecraft Orbit [M]. Changsha: National University of Defense Technology Press, 2003 .(in Chinese)

[11] 袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,1997.

YUAN Ya-xiang,SUN Wen-yu. Optimization Theory and Methods[M]. Beijing: Science Press,1997.(in Chinese)