多分类器融合的快速高维特征聚类图像分割*

黄荣顺1，吴宏刚1，刘思远

(1.中国民用航空局 第二研究所，成都 610041；2.中兴通讯 成都研究所，成都 610041)

1 引 言

图像分割可认为是多维特征向量的分类问题，对图像进行分割也就是对表达像素特征的多维特征进行分类。为了完整表达图像中像素的特征，进行聚类的多维特征向量必然包括像素的灰度或颜色特征、像素空域约束特征及运动特性等特征(在本文中，由于研究的重点是静止图像的分割问题，因此我

们忽略了像素的运动特征)。在多维数据的分类方法中，模糊C均值聚类算法(FCM)[1]由于引入了体现人类认知特性的模糊隶属度的概念，在图像分割中得到了非常广泛的应用，但由于在传统FCM算法中，聚类特征只有像素的灰度或颜色特征，并没有充分考虑到像素间的空域约束特征，因此FCM算法聚类的特征是不完整的，不能取得令人满意的分割效果。

针对FCM算法以上缺点，许多学者提出了改进的聚类算法[2-3,7]。文献[2]提出了基于Gibbs随机场的FCM算法(GFCM),它使用单分类器进行分类，将Gibbs随机场描述的空域约束信息以乘积的形式引入到FCM目标函数中。与GFCM的单分类器分类方式相似，文献[3]提出基于核函数距离测度以及空域约束的FCM算法(KFCM-S)，KFCM-S算法在FCM目标函数中以加和的形式引入了基于像素邻域均值的空域约束条件。虽然文献[2，3]中的算法在图像分割时考虑了空域约束关系，一定程度上解决了FCM存在的问题，但也增加了计算的复杂性，延长了计算时间。

与文献[2，3]的单分类器分类方法不同，本文提出一种多分类器融合快速高维特征数据分类图像分割算法。我们将高维特征数据分类问题分解为多个低维特征数据的分类，即基于灰度及颜色特征的最佳模糊分类以及基于空域约束的统计分类。通过多分类器融合的方法将不同分类器得到的分类结果进行整合，得到最后的分类结果。实验证明：本文算法不仅在分割性能上优于GFCM、KFCM-S算法，并且在计算时间上大大快于以上两种算法。本文第二节给出了快速高维特征数据聚类图像分割的理论模型及系统结构设计，第三节讨论了系统中的关键技术，第四节给出了实验结果及其分析。用了Dechirping技术及FFT快速算法，不但所需器件简单易行，而且测量精度及实时性较好，并可同时对多个通道间的相对时延进行测量。理论分析及仿真结果证明了这种测量方法的有效性。

2 理论模型

设图像y={yij|(i,j)∈I}，其中yij为像素点(i,j)的灰度(颜色)特征，二维点阵I={(i,j)|i∈[1,M],j∈[1,N]}为图像的支持域；欲将图像分为K类，需要对表达像素特征的高维特征向量fij=(yij,sij),(i,j)∈I进行分类，其中sij为像素点(i,j)的空域约束特征。在这里，我们定义sij为：图像中除点(i,j)外，其余像素点的分类情况。由于空域约束特征sij与图像中其它像素的分类情况相关联，因此如果直接对特征向量fij进行聚类，其计算过程十分复杂。为降低复杂性，我们将高维特征向量fij的聚类问题分解为yij和sij两个低维分量的聚类。因为像素的灰度或颜色是其最直观的特征，因此我们首先对特征yij进行最佳模糊聚类。对于空域特征sij的分类则较为复杂，我们首先基于最佳模糊分类的结果获得了图像空域约束特征sij，然后根据图像的空域统计约束准则得到基于空域约束特征sij的统计分类器。为了充分利用不同分类器的优点，我们将这两类分类器进行多分类器融合，然后根据分类器融合的结果进行图像分类。基于以上讨论，建立图像分割模型如图1所示。

图1 快速高维特征数据聚类图像分割模型

3 关键技术分析

3.1 像素灰度(颜色)最佳模糊分类器设计

为提高分类速度，在本文中，我们使用加权FCM[4]算法快速得到像素灰度(颜色)最佳模糊分类器Uopt。在加权FCM算法中，分类的样本为灰度或颜色特征yl,l∈[1,L]，其中L为灰度级数或颜色数， 欲将图像分为K类，构造加权FCM模糊聚类目标函数如下：

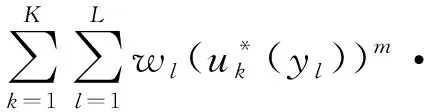
(1)

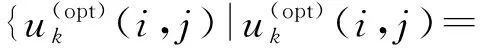
(2)

由此，可得最佳模糊分类准则：

(3)

其中，xij表示像素点(i,j)的分类状态。

3.2 空域约束特征获得

经过最佳模糊分类器，我们可以得到图像的具体分类情况x={xij|xij∈r,(i,j)∈I}。因为像素点(i,j)的空域约束特征sij定义为：图像中除点(i,j)外，其余像素的分类情况，因此可得sij为

sij={xmn|(m,n)≠(i,j),(m,n)∈I},
(i,j)∈I

(4)

3.3 空域约束统计分类器设计

图像分割中的空域约束准则可描述为：像素的分类由图像中其它像素的分类状态所决定。设随机场X={Xij|(i,j)∈I}为定义在I上的分类状态随机场，其中：离散随机变量Xij表示像素点(i,j)的所属类别，其取值空间为类别集合r；设随机场Xij={Xmn|(m,n)≠(i,j),(m,n)∈I}为点(i,j)的分类约束随机场。根据图像分类的空域约束准则，后验概率P(Xij=k|Xij=sij),(i,j)∈I描述了像素分类的空域约束力大小，因此我们选择其作为空域约束分类器的分类测度函数，则分类判决准则为

(5)

下面，着重讨论后验概率P(Xij=k|Xij=sij)的计算方法。根据贝叶斯公式可得：

P(Xij=k|Xij=sij)=P(Xij=k,Xij=sij)/

P(Xij=sij)

(6)

在本文中，我们认为像素的分类只决定于其邻域像素点的分类状态，因此图像分类随机场X可视为定义在邻域系统η上的Markov随机场。根据Hammersley-Clifford 定理[4]，X的联合分布概率为

P(X=x)=1/Z·e-U(x)

(7)

(8)

因此，根据式(5)、(6)、(7)可得：

(9)

(10)

由式(8)、(9)可得,后验概率P(Xij=k|Xij=sij)为

(11)

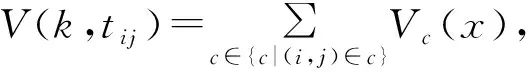
V(k,tij)=I(k,t1)+I(k,t2)+I(k,t3)+I(k,t4)+

I(k,t5)+I(k,t6)+I(k,t7)+I(k,t8)=

8-Nk

(12)

式中，Nk为在(i,j)的邻域中类别取值为k的点的个数。

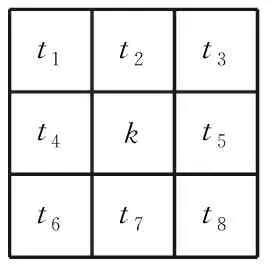
t1t2t3t4kt5t6t7t8

根据式(10)、(11)，可得：

(13)

为表达简单，将后验概率P(Xij=k|Xij=sij)记为Pk(i,j)，根据式(13),可得空域约束后验概率测度矩阵：P={Pk(i,j)|k∈r,(i,j)∈I}。

3.4 多分类器融合

为了充分发挥不同分类器的优点，我们将最佳模糊分类器及空域统计约束分类器进行多分类器融合[6]，得到优化的分类结果。在这里，我们使用线性加权的方式进行多分类器的融合，其融合后的分类测度函数为

(14)

多分类器融合的分类准则为

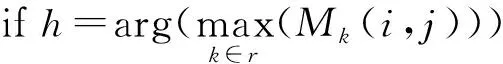
(15)

从式(14)可以发现，融合参数αk、βk直接影响着最后的分类性能，当αk=1、βk=0时，复合分类器退化为标准的FCM模糊分类；当αk=0、βk=1时，复合分类器变为空域统计约束分类；在本文中，我们采用试验的方法确定αk、βk的值。

4 实验结果及其分析

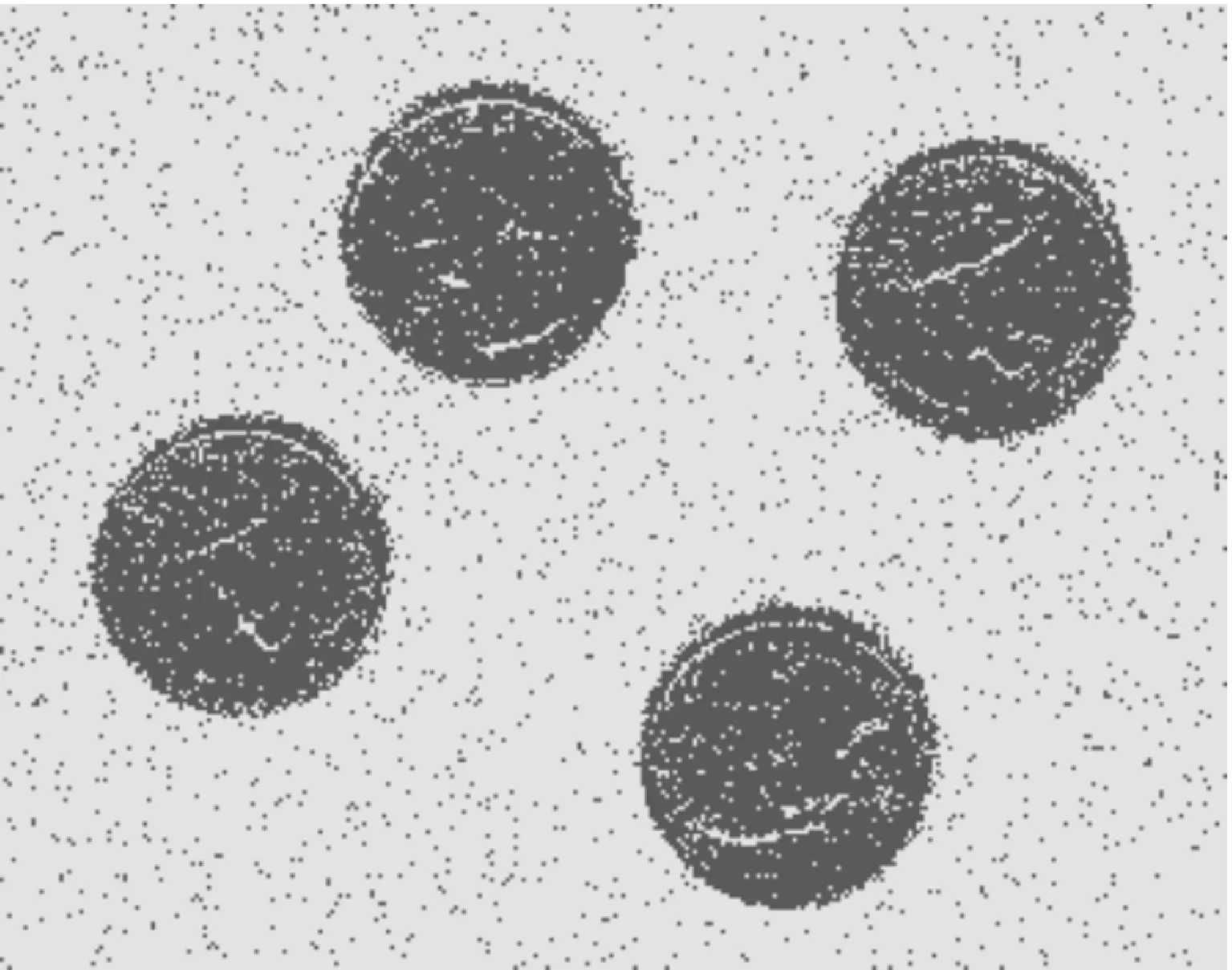
图3显示了对于真实图像的分割结果比较。图3(a)为受到椒盐与高斯混合噪声污染的真实图像，其分类数K=2；其中图3(b)为最佳模糊分类器的分类结果；图3(c)为空域约束统计分类器的分类结果；图3(d)为GFCM算法分类结果；图3(e)为KFCM-S算法分类结果；图3(f)为多分类器融合的分类结果，其中分类器融合系数αk=0.33,βk=0.65,k=1,2。

从图3中可以发现：最佳模糊分类抵御噪声的能力最差，其分类的结果也最差，而其余方法均取得了较好的分类效果。相比之下，KFCM-S算法与多分类器融合的分类结果最好。

我们对50幅大小为217×181、噪声水平为1%～9%的脑部MR T1加权图像进行了分割性能测试，图4显示了部分实验结果。其中，图4(a)为噪声水平为7%的脑部MR T1加权图像，其分类数K=3；图4(b)～(f)与图3(b)～(f)相似，分别为5种不同分类器的分类结果，其中多分类器融合的融合系数为：αk=0.5,βk=1.55,k=1～3。

(b)最佳模糊分类器的分类结果

(c)空域约束统计分类器的分类结果

(d)GFCM算法分类结果

(e)KFCM-S算法分类结果

(f)多分类器融合的分类结果

从图4中可以发现与图3类似的结果，与最佳模糊分类相比其余4种分类算法均有效地抑制了噪声的影响，在总体上，多分类器融合与KFCM-S算法要略好一些。在图像分类细节的保护上，不同算法之间有着较大差异。图4(c)～(f)中黑色圆圈所圈示的部分显示了不同算法对于分类细节的保护情况。在图4(c)、(d)中由于强调了图像分类的连通性，其分类细节未得到很好的保留，而在图4(e)、(f)中, 多分类器融合算法与KFCM-S算法则很好地保护了图像分类的细节信息。表1显示了不同分类算法在不同噪声水平下平均正确分类率的比较。

从表1中可以发现：随着噪声水平的增加，各种分类算法的性能均有所下降，但FCM算法下降的最快，而快速高维特征数据聚类算法的性能在不同噪声水平下均略优于其它算法。

表2显示了不同算法对于脑部MR T1加权测试图像平均计算时间的比较。

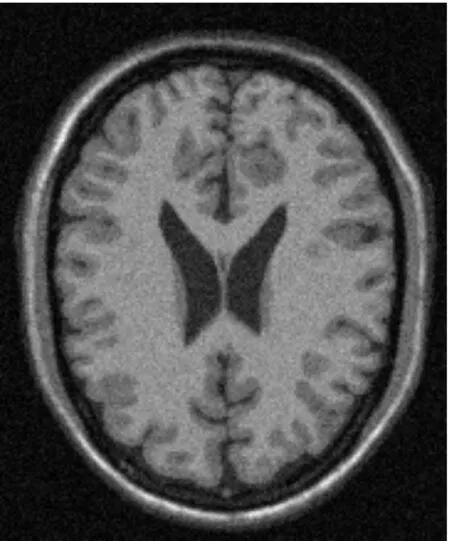
(a)脑部MR T1加权图像

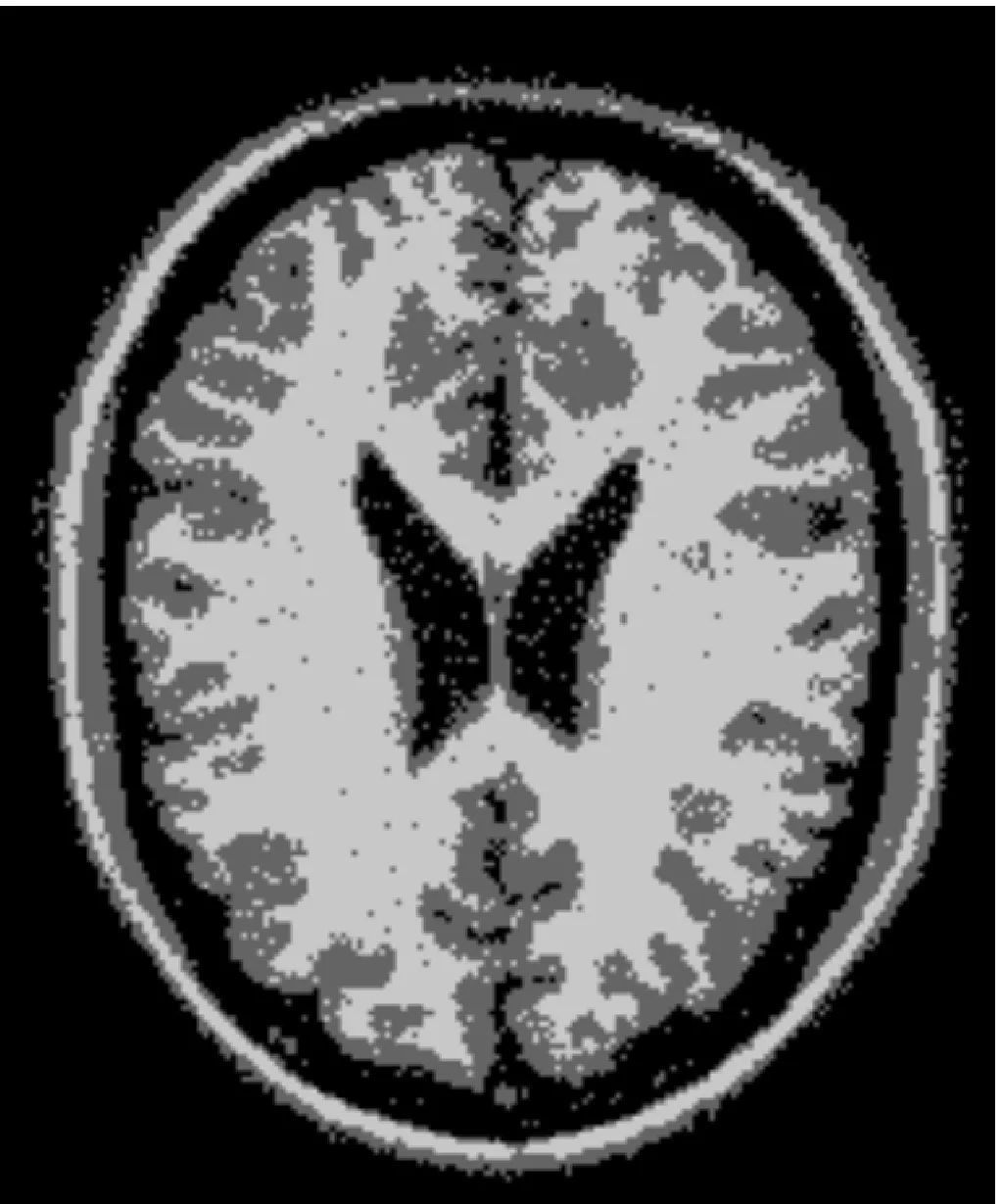
(b)最佳模糊分类器的分类结果

(c)空域约束统计分类器的分类结果

(d)GFCM算法分类结果

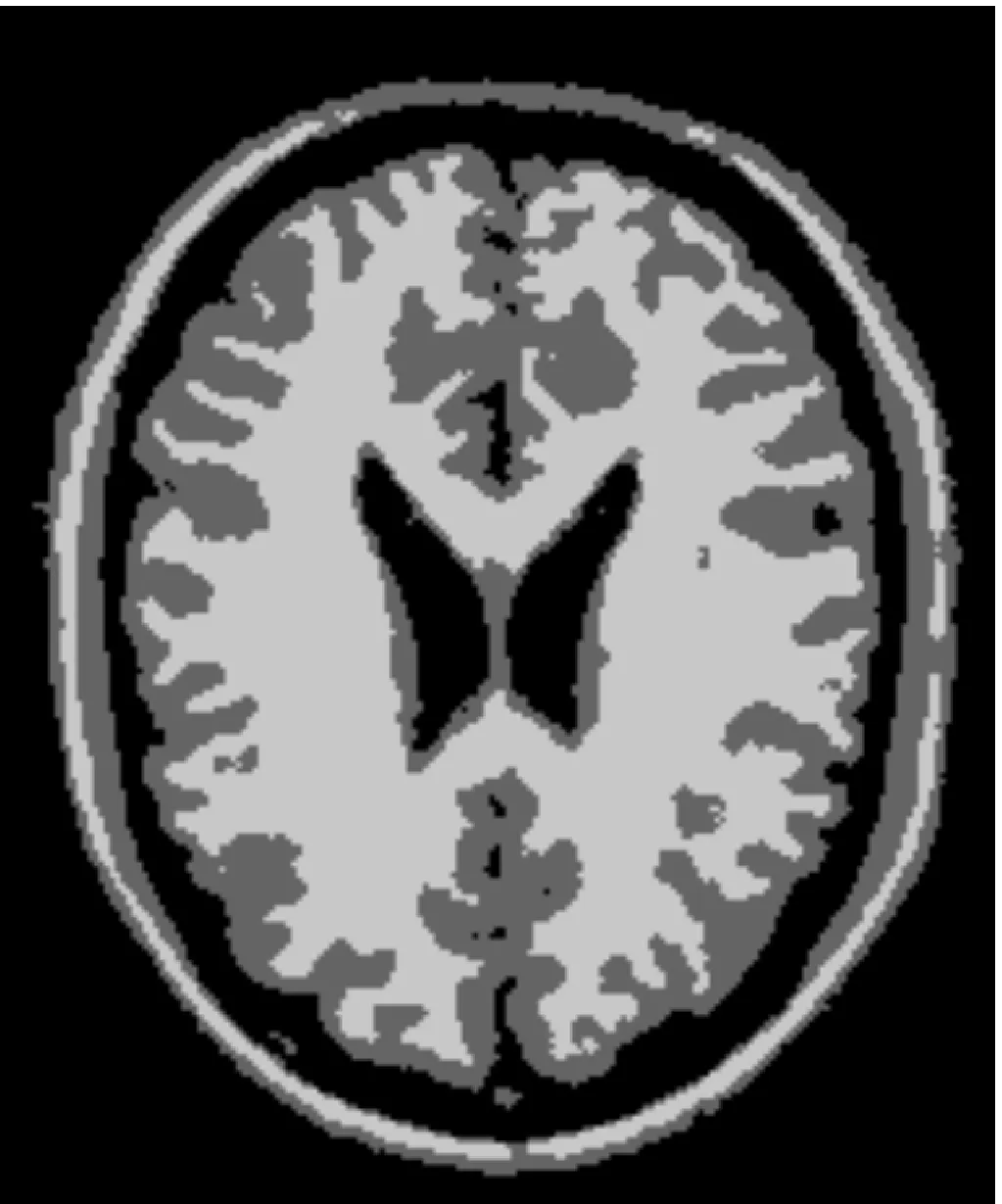
(e)KFCM-S算法分类结果

(f)多分类器融合的分类结果

表1 算法平均正确分类率比较Table 1 Comparison of mean accuracy rate for clustering %

表2 算法平均计算时间的比较Table 2 Comparison of mean time cost s

由表2可以发现：快速高维特征数据聚类算法在计算速度上明显优于GFCM与KFCM-S算法，与FCM算法接近。从图3、4及表1、2中可以得出：与其它分类方法相比，快速高维特征数据聚类算法有着很好的分割性能，并且大大提高了计算速度。

5 结 论

本文提出一种多分类器融合快速高维特征数据分类图像分割算法，将基于高维特征数据聚类的图像分割问题分解为多个低维特征的分类问题，并通过多分类器融合将各低维分类器的分类结果进行整合，从而得到最后的分类结果。实验结果表明：在拥有更好分割性能的同时，本文提出的算法保持了计算的简捷性，提高了算法的实用性，在图像分割中取得了较好的效果。今后的工作将集中在多分类器融合参数αk、βk及分类数目的自适应选择上。

参考文献：

[1] BEZDEK J C.Pattern recognition with fuzzy objective function algorithms[M]. New York:Plenum Press,1981.

[2] 冯衍秋，陈武凡,等. 基于Gibbs 随机场与模糊C均值聚类的图像分割新算法[J]. 电子学报, 2004, 32(4)：645-647.

FENG Yan-qiu, CHEN Wu-fan, et al. A New Algorithm for Image Segmentation Based on Gibbs Random Field and Fuzzy C-Means Clustering[J]. Acta Electronica Sinica, 2004, 32(4)：645-647.(in Chinese)

[3] CHEN S, ZHANG D. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure[J]. IEEE Transactions on Systems, Man and Cybernetics ,2004, 34(4): 1907-1916.

[4] 高新波，李洁，姬红兵. 基于加权模糊c均值聚类与统计检验指导的多阈值图像自动分割算法[J]. 电子学报, 2004，32(4):661-664.

GAO Xin-bo, LI Jie,JI Hong-bing. A Multi-threshold Image Segmentation Algorithm Based on Weighting Fuzzy c-Means Clustering and Statistical Test[J]. Acta Electronica Sinica, 2004, 32(4):661-664.(in Chinese)

[5] DERIN H, ELLIOTT H. Modeling and segmentation of noisy and textured images using gibbs random fields[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1987(1):39-55.

[6] KITTLER J, HATEF M, ROBERT P W, et al. On combining classifiers[J]. IEEE Transactons on Pattern Analysis and Machine Intelligence, 1998，20(3):226-239.

[7] 武小红，周建江. 可能性模糊C-均值聚类新算法[J].电子学报， 2008, 36(10):1996-2000.

WU Xiao-hong, ZHOU Jian-jiang. A Novel Possibilistic Fuzzy C-Means Clustering[J]. Acta Electronica Sinica, 2008, 36(10) : 1996-2000.(in Chinese)