基于短时傅里叶变换的相位编码信号分析*

(中国西南电子技术研究所，成都 610036)

1 引 言

在现代战争中，辐射源的识别对许多重大战略决策具有重要的指导意义。随着新体制雷达的不断出现和雷达信号形式的日益复杂，传统的分析方法己经不能满足电子侦察的要求。电子对抗除了要求对雷达信号进行常规的分析，如到达时间、到达角、载频、脉冲宽度、脉冲重复频率和极化方式等之外，还必须对雷达信号脉内细微特征进行分析和提取，以便有效地识别雷达信号，判断目标的威胁程度。因此，详细分析雷达信号的各种细微特征，包括脉内、脉间和脉组的细微特征及有意和无意的调制，将为雷达信号的分选和识别提供有力的帮助。

雷达信号脉内调制特性分析起源于21世纪80年代初，国内外已经作了大量的研究，有多种估计算法和相关技术,主要包括谱相关分析法、调制域分析法、数字中频处理法[1-2]等。在有些应用场合，如要求准确识别相同相位编码调制样式的信号时，仅仅知道其调制样式是不够的，还必须对编码序列进行恢复，从而准确判断出具有相同调制样式但具有不同编码序列的信号。因此，上述方法还存在一定缺陷。

由于相位编码信号在相位跳变处有突变特性，本文提出的利用短时傅里叶变换(STFT)得到信号的时频分布，通过相参积累的方法找到相位编码信号的跳变位置，从而检测码元；最后，通过分析跳变位置处相位的变化情况，恢复得到编码信息。该方法的优势在于在较低信噪比情况下也可以得到较好的解码结果，在工程上有一定的应用价值。

2 算法原理

2.1 短时傅里叶变换

对于时间信号f(t)，其窗口Fourier变换定义为

(1)

当窗口函数满足一定的标准化条件时，具有反演公式：

(2)

满足窗口函数条件为：t·g(t)∈L2(R)和g(t)∈L2(R)的窗口Fourier变换称为短时傅里叶变换，二维函数F(ω,τ)(-∞<ω<∞,-∞<τ<∞)反映了信号f(t)在时刻τ附近的局部频谱特征，随着τ的推移，F(ω,τ)刻画了信号f(t)在时、频两域的信息。

STFT是通过窗函数g(t)将一维信号f(t)映射成时间-频率域上的二维函数。它的主要优点是若信号f(t)在给定的时间间隔和频率间隔内具有大多数能量，则其STFT将局域化于该区域内；而在信号没有多少能量的时间和频率间隔处，其STFT接近为0；其主要的缺陷在于对所有频率都使用单一的窗函数，所以STFT的分辨率在时间-频率域内处处相同。

2.2 滑动窗的短时傅里叶变换递归算法

在实际应用中，需要对式(1)进行离散化，同时为了得到信号的时频特性，还要对信号进行滑动取值。设x(m)与g(m)(m=0,1,2,…)分别为离散时间信号与窗函数，设选取窗口长度为L，则有：

令

则：

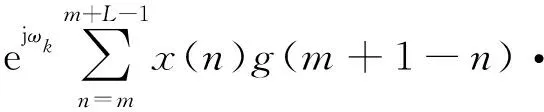
e-jωk(n-m)-x(m)g(1)ejωk+

x(m+L)g(L-1)e-jωk(L-1)=

[T(m,k)-x(m)g(1)]ejωk+

x(m+L)g(L-1)e-jωk(L-1)

(3)

式中，代表时间标尺的m在样点范围[0，N-1]内滑动取值；L为计算STFT的时间窗长度；频率点ωk在信号频率范围[2π(f0-B/2),2π(f0+B/2)]内等间隔取样。因此利用递归算法，滑窗STFT与小波变换等方法比较，可以大大提高运算速度。

2.3 相位编码信号码元检测

要获得相位编码信号的码元检测曲线，需要利用短时傅氏变换的结果求出相邻数据段之间的相参性。为此，定义如下时间序列作为信号的瞬时相参度指标：

η(m)=|T(m,ωa)|+|T(m+L,ωb)|-

|T(m,ωc)+T(m+L,ωc)e-jωcL|

(4)

式中，ωa、ωb分别为|T(m,ωk)|和|T(m+L,ωk)|的峰值频率，而ωc的取值为

(5)

从以上定义可见，η(m)在信号相位出现不连贯突变时刻呈现出峰值。因此，通过对η(m)序列进行峰值检测，即可以检测出码元及其边缘位置(时刻)。门限可以根据η(m)中的最大值ηmax由经验来确定。

2.4 相位的估计

要恢复相位编码信号的编码序列，需要获得跳变点处的相位信息。为适应较低的信噪比要求，可将长脉冲数据按样点数L均匀分割成M段，对每段进行相关积累以提高信噪比。假设已经粗测得信号的频率为fc，对各段信号进行相关积累如下：

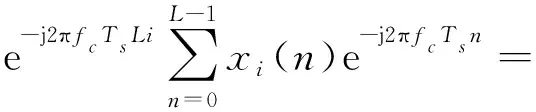
L·Aej(φi-2πfcTsLi+θ)+ni

(6)

式中，θ=π(fo-fc)(L-1)为常量，ni为混在信号中的噪声分量的谱相关结果。对于常规信号，由于第i段数据的初相φi=φo+2πfoTsiL，因此，yi可表示为

yi=L·Aej(φo+θ+2π(fo-fc)TsiL)+ni=

L·Aej(β0+2πfΔTsiL)+ni

(7)

式中，相位常量β0=φo+θ，频率残差fΔ=fo-fc。测量yi的相位并解相位模糊得：

βi=β0+2πfΔTsiL,i=0,1,2，…,M-1

(8)

利用最小均方误差准则由式(8)可以估计频率残差分量和初相，其估计式为

(9)

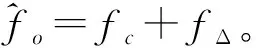
2.5 相位编码信号分析

对PSK信号的分析主要利用测量到的码元初相参数，同时也必须利用频率测量结果来进行时间上的同步。总结以上分析可得解码步骤如下：

(1) 求出频率序列的平均频率作为信号的中心频率；然后从第一个码元初相测量值开始，根据中心频率预测下一码元的初相，与该码元的实测值相减，得到相邻码元的相位差序列；

(2) 令第一个码元的符号为零，下一个码元符号则根据它与前面码元的相位差来确定，若相位差是π/2的k倍(四舍五入)，则其符号为上一码元符号加上k；

(3) 依此往下推，解算出所有码元；

(4) 对所有码元按4取模运算，将符号值调整在0～3之间；

(5) 检测编码符号中是否有1或3，如果无则信号被识别为二相编码信号，并将所有符号除以2，得到二相编码信号的解码；如果有，则信号被识别为四相编码信号，其解码结果不变。

3 仿真实验

3.1 相位编码信号分析结果

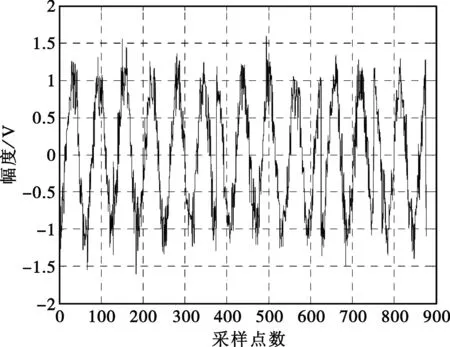
图1 10 dB BPSK信号

图2 短时傅里叶变换结果

图3 检测码元跳变点曲线

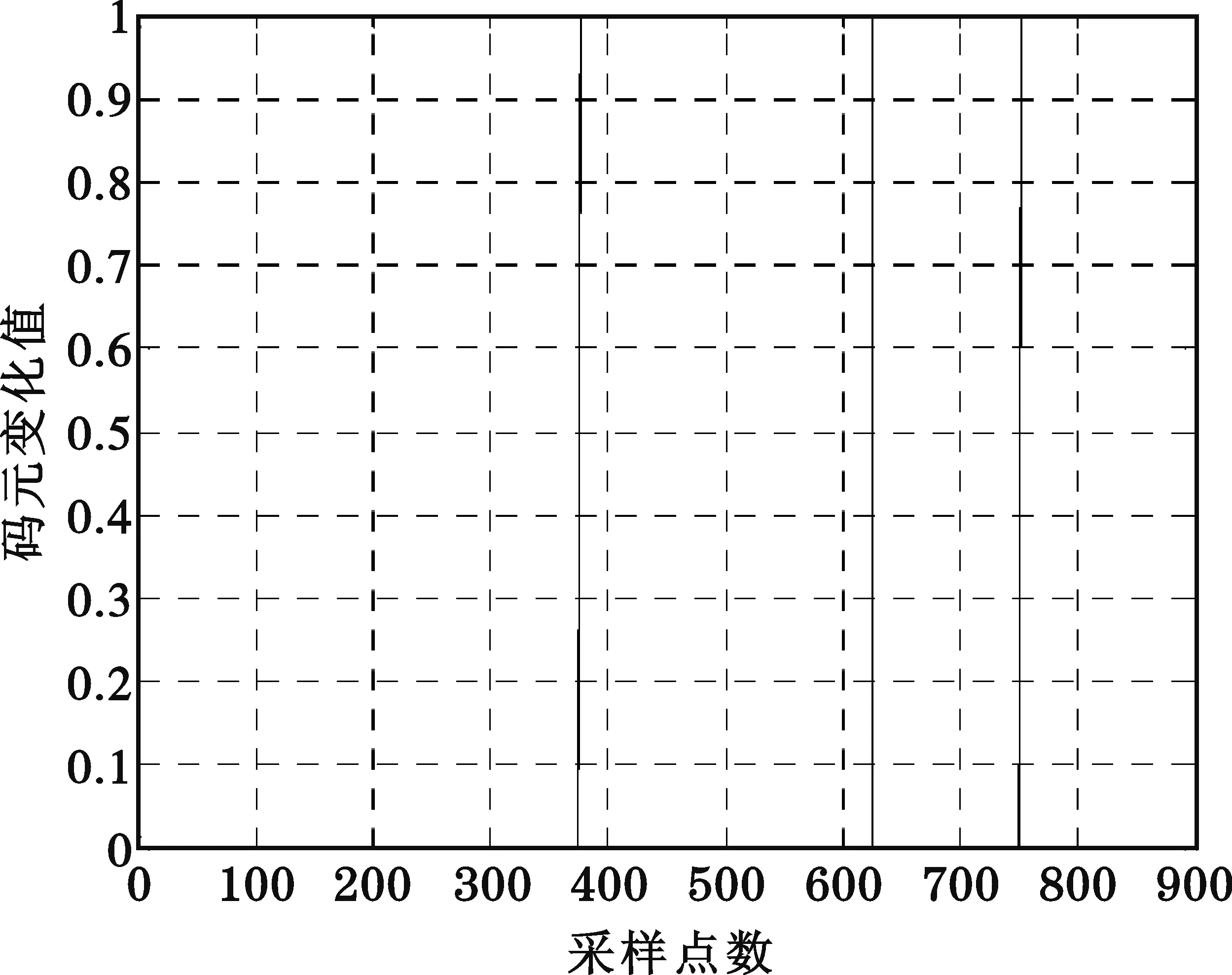
图4 解码结果

为了验证方法的有效性，我们分别对BPSK和QPSK信号进行了仿真分析。图1～4是BPSK信号的分析结果，其中BPSK信号选用了7位Barker码，信号载频4 MHz，码宽0.5 μs，采样频率为250 MHz，信噪比为10 dB。

图5～8是QPSK信号的分析结果。其中QPSK信号选用了16位Frank码，信号载频4 MHz，码宽0.5 μs，采样频率250 MHz，信噪比10 dB。

由图1～8可以看出，该方法能够在较低信噪比情况下实现对相位编码信号的频率测量和解码。

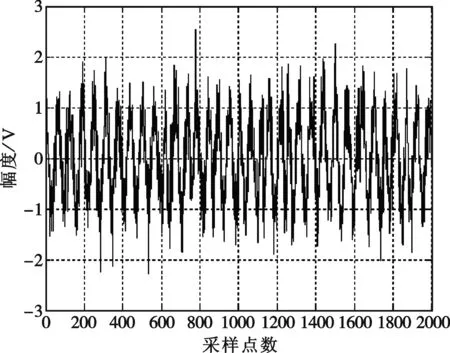
图5 10 dB QPSK信号

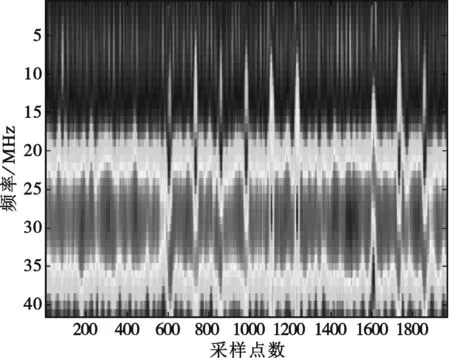
图6 短时傅里叶变换结果

图7 检测曲线

3.2 窗函数选择对算法的影响

为了分析短时傅里叶变换中窗函数对算法的影响，我们在不同信噪比和不同窗函数条件下分别对BPSK和QPSK信号进行了蒙特卡罗试验。我们选取较有代表性的窗函数，包括矩形窗、汉明窗、Blackman窗、切比雪夫窗和Kaiser窗，最后统计得到解码正确率，如图9和图10所示。

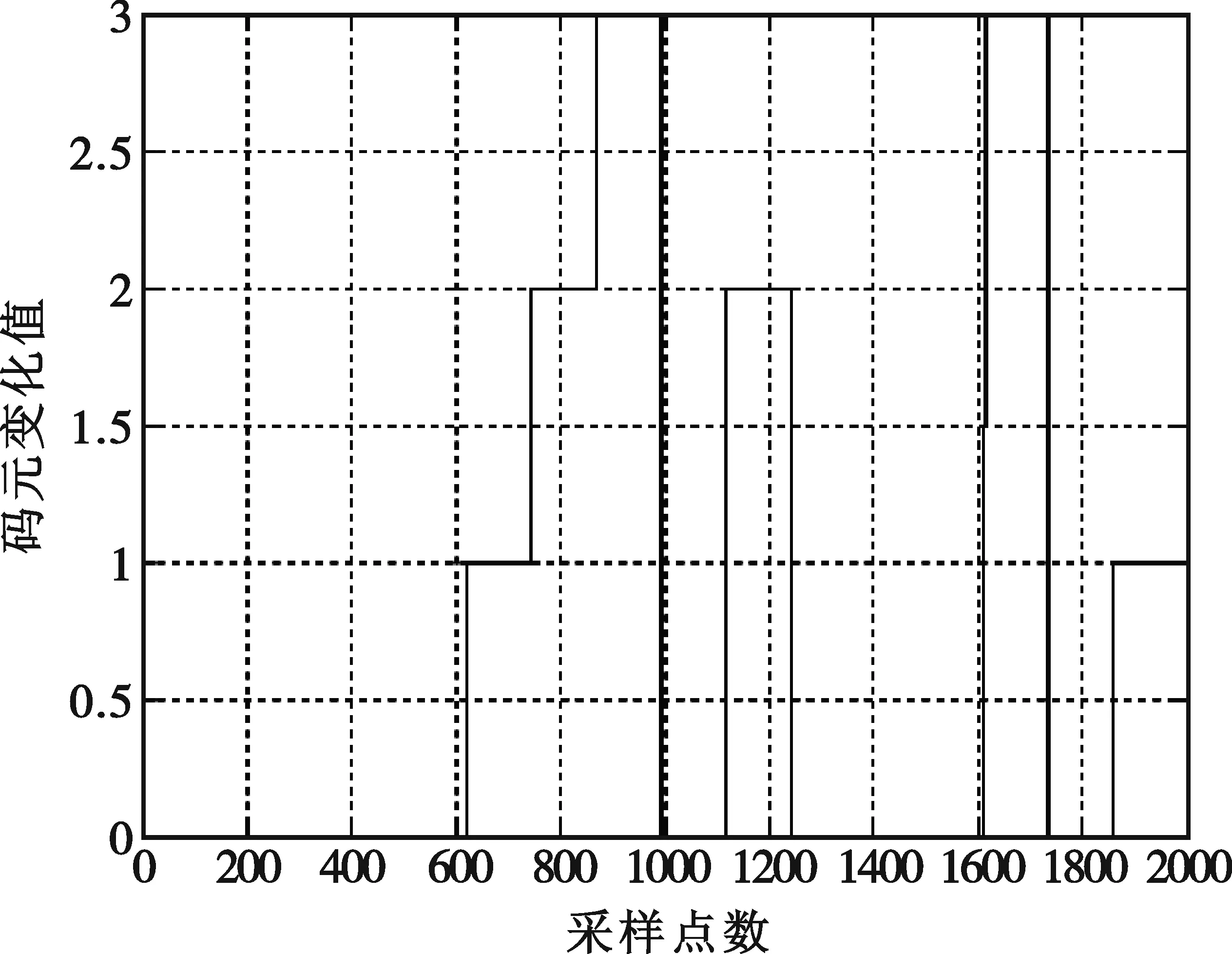
图8 解码结果

图9 BPSK信号解码正确率与窗函数的关系

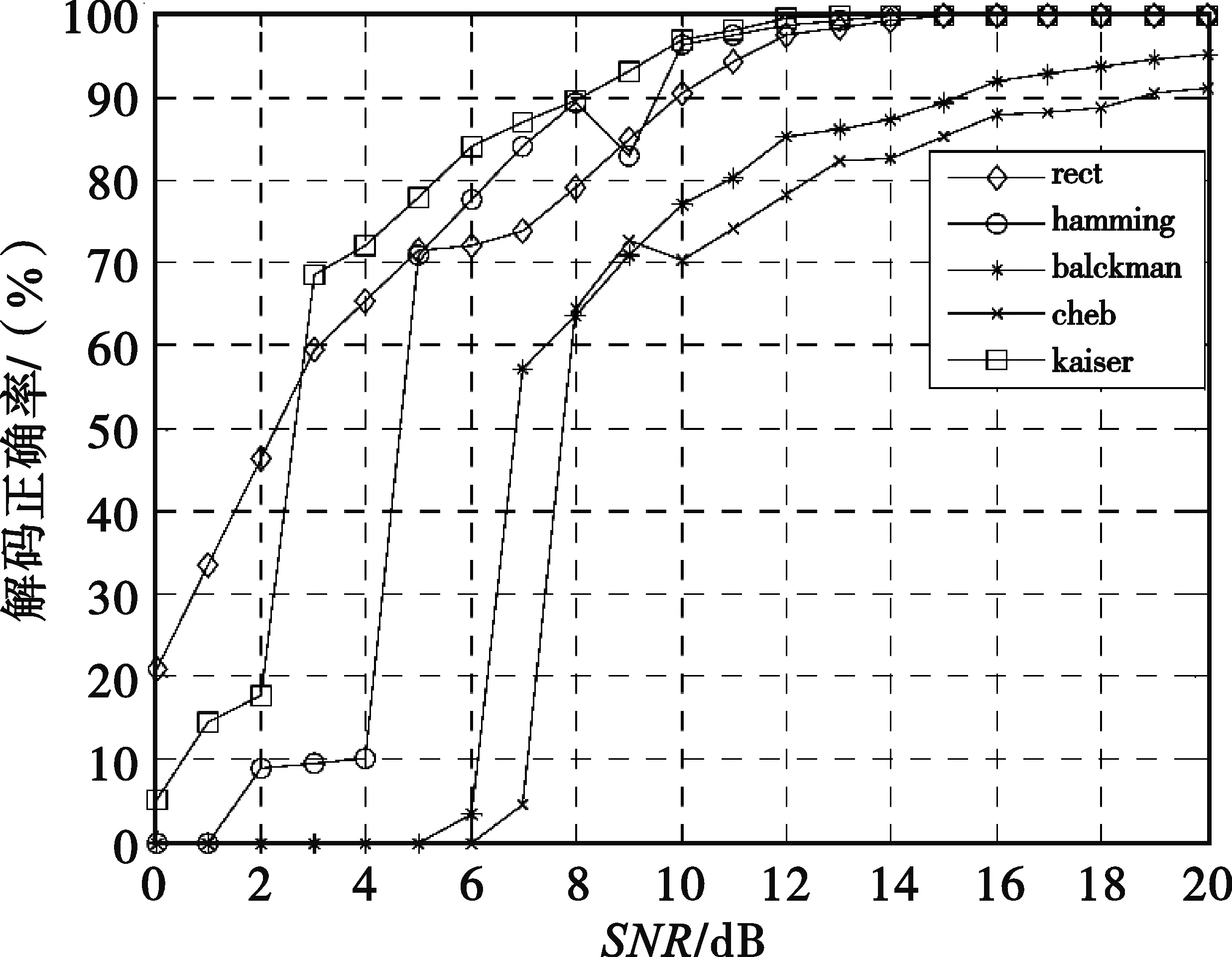
图10 QPSK信号解码正确率与窗函数的关系

由图可见，窗函数的选择对算法有一定影响，通过选择合理的窗函数如汉明窗，能够进一步降低算法对信噪比的要求。

4 结 论

本文根据相位编码信号在相位跳变处的突变特性，采用短时傅里叶变换(STFT)结合相参积累的算法找到相位编码信号的跳变位置，从而检测到码元；然后通过分析相位在跳变位置处相位的变化情况，恢复得到编码信息。该方法与时频分布、小波变换等方法比较，处理速度较快，在较低的信噪比情况下也可以得到较好的处理结果，在雷达信号细微特征分析等方面有一定的工程应用价值。

参考文献：

[1] 黄知涛,周一宇. 一种有效的BPSK/QPSK信号调制识别方法[J]. 电子对抗技术, 2005, 20(2): 10-13.

HUANG Zhi-tao,ZHOU Yi-yu.An Effective Approach to the Recognition of BPSK/QPSK Signals[J].Electronic Warfare Technology,2005,20(2):10-13.(in Chinese)

[2] 赵冰,罗丰,吴顺君. 相位编码信号的谱相关分析与调制参数估计[J]. 雷达与对抗,2005(3):34-37.

ZHAO Bing,LUO Feng,WU Shun-jun.Spectral Correlation analysis and moducation Parameor Estimation of PSK Signals[J].Radar&Ecm,2005(3):34-37.(in Chinese)

[3] 穆世强，熊健，陈天麒. 脉内调制特性的中频解调分析[J].电子科技大学学报,1993, 22(3):237-242.

MU Shi-qiang,XIONG Jian,CHEN Tian-lin. Analysis of IF Demodulation with intra-pulse Modulation Characteristics[J].Joural of University of Electronic Technology of China,1993,22(3):237-242.(in Chinese)