准完全重构余弦调制滤波器组的最优化设计*

(解放军信息工程大学 信息工程学院，郑州 450002)

1 引 言

完全重构(PR)滤波器组和准完全重构(NPR)滤波器组在信号处理中有着非常重要的应用。余弦调制滤波器组(CMFBs)是滤波器组中比较高效的一种，其设计和实现的复杂度相对较低，并且具有极好的频率选择性。PR或者NPR系统的设计通常是通过非线性约束优化的迭代算法实现。当变量和约束的数目增加时，最优化算法对原型滤波器的初始值相当敏感。因此,需要对原型滤波器的设计方法和初始值的选取原则进行深入研究，以获得更快的迭代收敛速度和更好的性能[1]。

设计高阻带衰减的原型滤波器是设计PR滤波器组的难点。事实上，即便是能够得到满足要求的原型滤波器，其设计过程也相对较为复杂。为满足完全重构和高阻带衰减的要求，原型滤波器的阶数通常会很大[2]。而原型滤波器阶数的增加在一定程度上增大了待优化的参数个数，同时加大了非线性优化的难度。如果适当放宽完全重构的条件，使用NPR滤波器组，则用较少阶数的原型滤波器即可获得高的阻带衰减。在重构误差可以接受的前提下，能使NPR滤波器组的运算量明显降低。NPR滤波器组具有更广泛的实用性,因此本文主要研究NPR滤波器组的设计问题。

在NPR滤波器组的设计方面，大多数的设计方法把重点放在了使用线性相位原型滤波器组的NPR CMFBs上。文献[3]中提出了一种低时延的NPR CMFBs的设计方法，在较少信道时能获得较小的滤波器长度。文献[4]提出了一种基于二阶锥规划的CMFBs设计算法。文献[5]采用了单参数优化的方法选择合适的等波纹原型滤波器设计CMFBs。本文在这些方法的基础上研究了使用过渡带具有平方根余弦滚降特性的原型滤波器设计NPR CMFBs的方法。这种原型滤波器是线性相位原型滤波器的一种改进。使用这种原型滤波器，可以更好的满足NPR CMFBs所需的幅度平坦条件，从而设计出具有低重构误差的滤波器组。本文把滤波器组的设计问题归结为一个凸极小极大最优化问题，用二阶锥规划算法可以得到最优化解[6]。设计结果表明本方法设计的NPR CMFBs的重构误差更小，并且有较大的阻带衰减。由于使用了平方根余弦滚降原型滤波器，滤波器组第一个和最后一个分析滤波器的通带波纹得到了有效的抑制。而这往往是普通的CMFBs设计方法中难以避免的问题[7]。

2 设计原理

CMFBs的原型滤波器的频率响应可以写作

P(ejω)=PM(ejω)e-jωD/2

式中,D/2是滤波器的设计群时延。对于一个M通道的NPR CMFBs，分析滤波器通过调制原型滤波器获得：

(1)

(2)

式中,k=0，1，…，M-1;n=0,1，…,N-1;p(n)是原型滤波器的冲激响应;N是原型滤波器的长度;D/2是系统时延。

要使得滤波器组重构有意义，必须保证其有正常的频带选择性，即通带平坦特性和阻带衰减特性。系统的传输函数[8]：

(3)

通过使|T0(ejω)|尽可能地接近一个常量可以使重构的幅度衰减达到最小。假设通带的波纹足够小，则分析滤波器的通带|T0(ejω)|值会接近常量，这一点容易满足。所以，我们主要考虑其过渡带。又因为Uk(ejω)和Vk(ejω)是P(ejω)频移的结果，我们只需要再加上一个保证其平坦性的约束条件[9]

|P(ejω)|2+|P(ej(2ωc-ω))|2=1

(4)

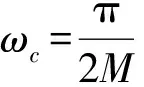
(5)

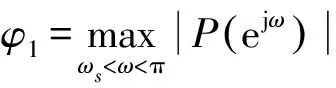
(6)

式中，D/2是系统的时延，Δω=ωs-ωp是过渡带宽，ω∈[-π,0]的理想响应Pd(ejω)=Pd(e-jω)。该滤波器的过渡带满足平方根余弦滚降特性。ω∈[ωp,ωs]时有：

|P(ejω)|2+|P(ej(2ωc-ω))|2=

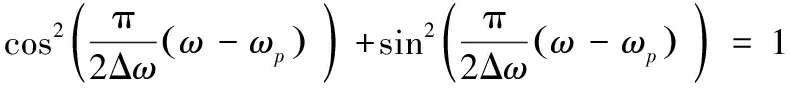
(7)

所以，使用这种原型滤波器，能够满足式(2)的平坦性条件。从设计实例可以看出，原型滤波器的平方根余弦滚降特性对于减小重构误差、抑制分析滤波器的通带波纹十分有效。

3 SOCP法设计原型滤波器的方法

本文的原型滤波器的设计问题可以SOCP算法来实现[10]。不失一般性，我们把复杂的设计问题看作是如下的极小极大判断准则：

Minimizeδ

Subject toW(ω)|P(ejω)-Pd(ejω)|≤δ

(8)

式中，-π≤ω≤π；δ是衡量最大波纹的一个补充变量；W(ω)是一个正的加权函数，用来调整不同频率的拟合紧密程度。为简化符号，原型滤波器的频率响应记为

(9)

式中，p=[p(0),p(1),…,p(N-1)]T是一个变量向量，c(ω)=[1,cos (ω),…,cos ((N-1)ω)]T，s(ω)=[1,sin (ω),…,sin ((N-1)ω)]T。设Pd(ejω)的实部和虚部分别为PR_d(ω)和PI_d(ω)，则式(8)可以进一步简化为

Minimizeδ

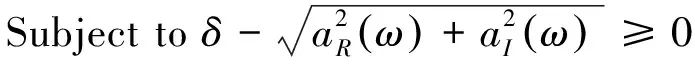
(10)

式中，aR(ω)=W(ω)[pTc(ω)-PR_d(ω)]，-π≤ω≤π，aI(ω)=W(ω)[pTs(ω)+PI_d(ω)]。要计算滤波器的频率响应，先需要将滤波器的连续频率响应离散化。离散化点数越多，设计精度越高，不过运算量也越大，因此在离散点数和计算量之间要折衷考虑。假设频率上的采样点为ωi(1≤i≤L)，这些频率点可以均匀或非均匀间隔,求解滤波器设计问题就是求解如下的标准SOCP问题:

MinimizebTy

Subject tobTy≥‖ci-Fiy‖2

(11)

式中，

ON是一个N行的零向量，‖·‖2表示欧式范数。这是一个凸最优化的问题，所以如果解存在的话可以保证一定是最优解。变量y的维数是N+1，采用约束的数目是L+1 ，约束越多得到的解越接近理想值，但是如果L>N，约束条件的冗余过多，可能造成算法不能收敛，所以一般取L=N。

用该方法设计的原型滤波器如图1所示，其中阶数N=512，理想截止频率ωc=π/32，过渡带宽Δω=π/64。设计过程中SOCP问题的求解采用了Matlab7.9和内点算法工具包SeDuMi1.21[11]。

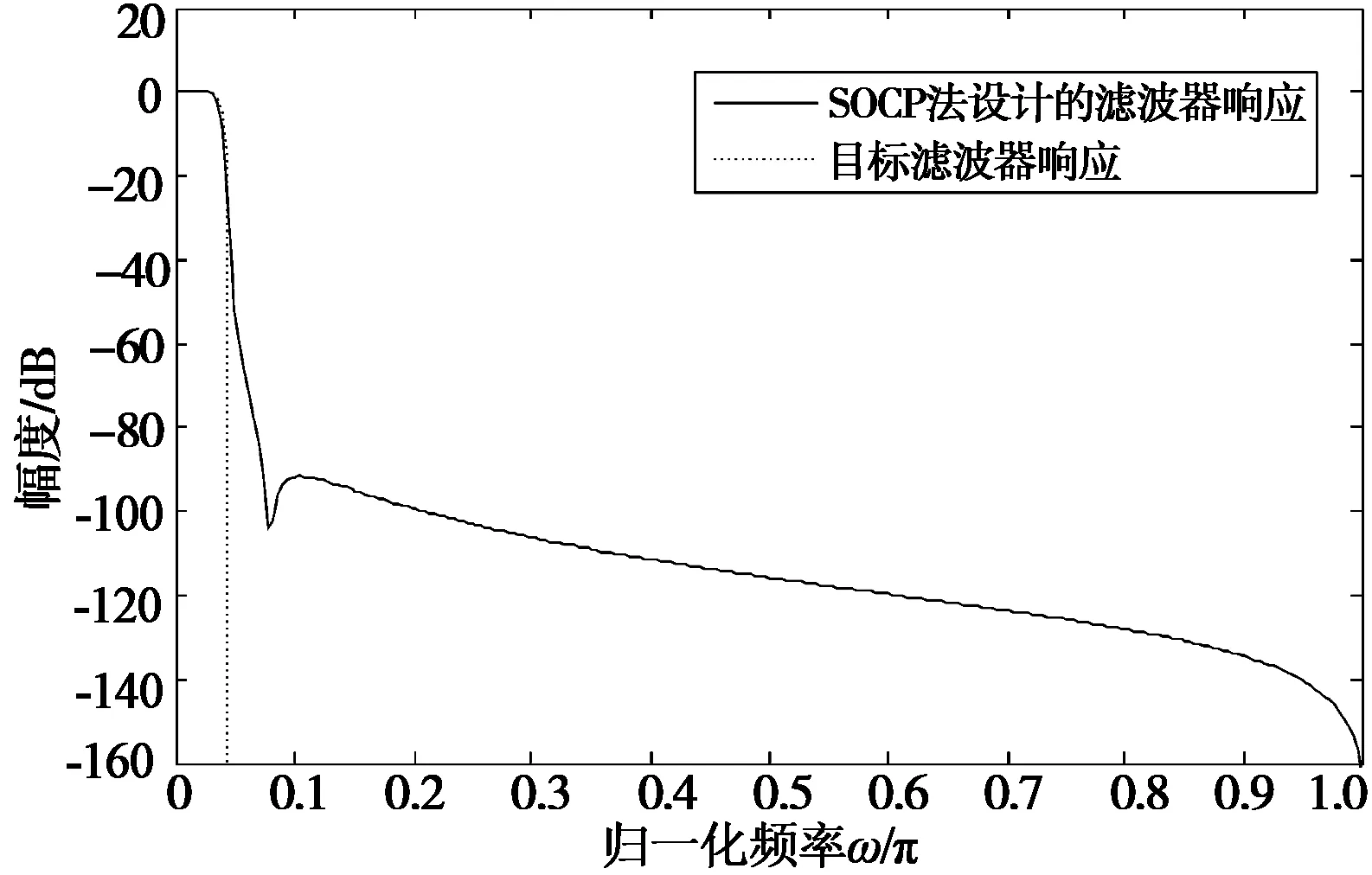
图1 SOCP法设计的原型滤波器Fig.1 Prototype filter designed by SOCP

4 NPR CMFBs的设计步骤和设计实例

原型滤波器的过渡带宽、通带波纹、阻带衰减和滤波器阶数需要折衷的考虑。一般通过优化过渡带宽和CMFBs的波纹可以进一步的提高NPR CMFBs的性能。式(4)的低通滤波器可以用上述SOCP算法设计。

设计过程中，使滤波器的设计误差ε最小即可保证通带波纹最小，对于给定的原型滤波器阻带衰减ds和设计误差ε0，可以通过反复调整通带过渡带宽和阶数N获得最佳的原型滤波器。设系统预设的阶数初始值是N0，最大允许的过渡带宽为Δω0。如果N0阶的滤波器满足设计误差和阻带衰减的要求，则采用N0阶的滤波器，并调整过渡带宽Δω使其最小；如果N0阶的滤波器不能满足设计误差和阻带衰减的要求，则采用过渡带宽Δω0，并调整阶数N使其最小。调整时采用二分法进行搜索，算法在调整步进ωstep或Nstep小于某个门限的时候停止迭代。

设计步骤描述如下：

(1)用给定的N0、Δω0、D设计式(6)的滤波器。计算重构误差ε和衰减d；

(2)如果步骤1的结果满足d>ds和ε<ε0，执行步骤3～4，否则执行步骤5～7；

(3)固定N=N0，令ωstep=Δω；

(5)固定Δω=Δω0，令N=2N，设计式(6)的滤波器。重复执行直至误差ε和衰减d满足d>ds和ε<ε0；

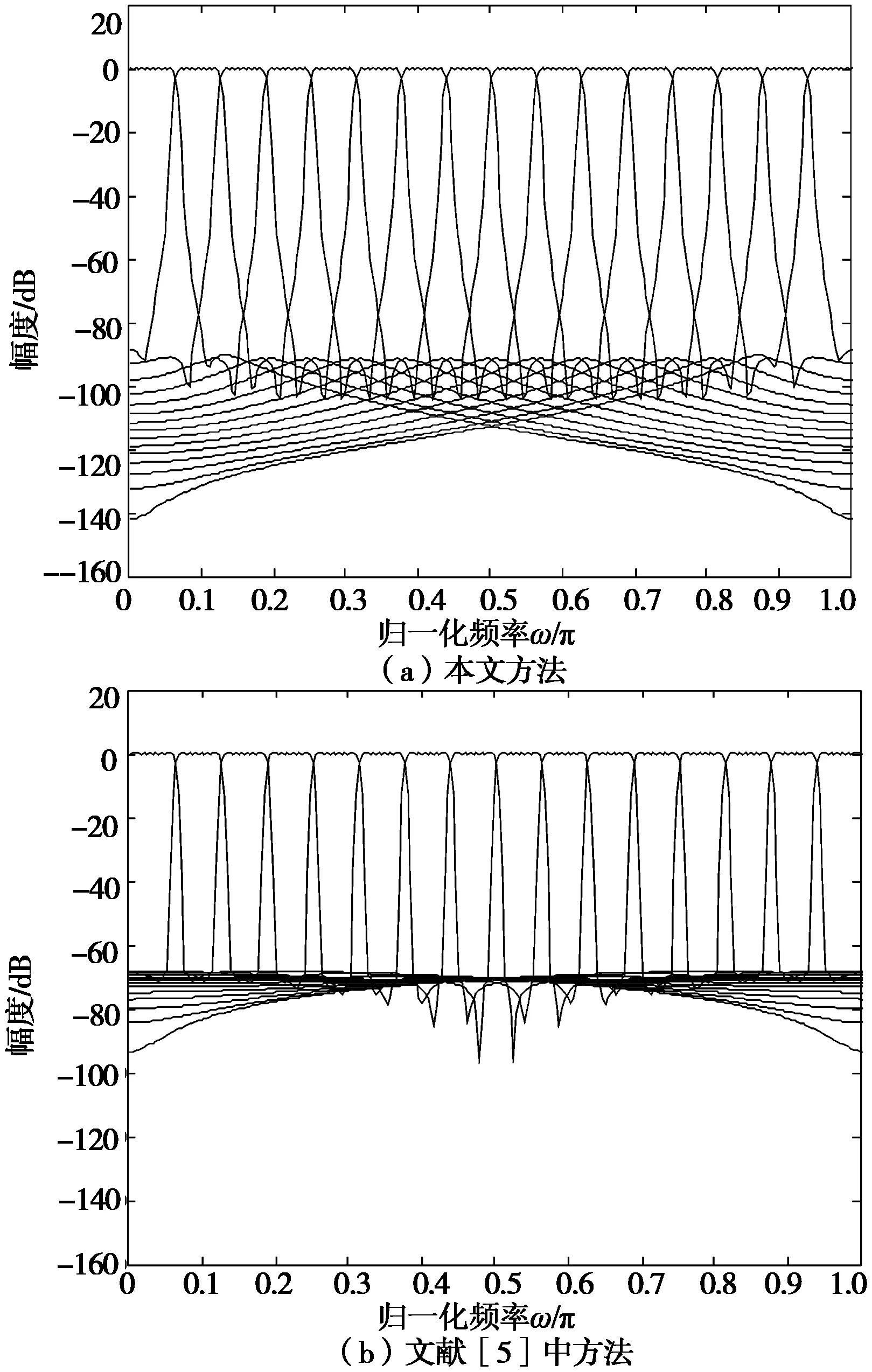
图2 余弦调制滤波器组分析滤波器Fig.2 Analysis filters of CMFBs

实验表明，使用本方法可得到满意的结果。图2、图3是用本文方法设计的滤波器组与使用文献[5]中单参数优化法设计的滤波器组的比较,两种方法取相同的阶数、过渡带宽和子带数等参数：N=512，Δω=π/64，M=16 。从实验结果可以看出,用本文方法能得到更小的重构误差和更大的阻带衰减。图4是用本方法设计的128信道的NPR CMFBs。实验表明,本方法在子带数目较大时依然能够获得满意的设计结果。

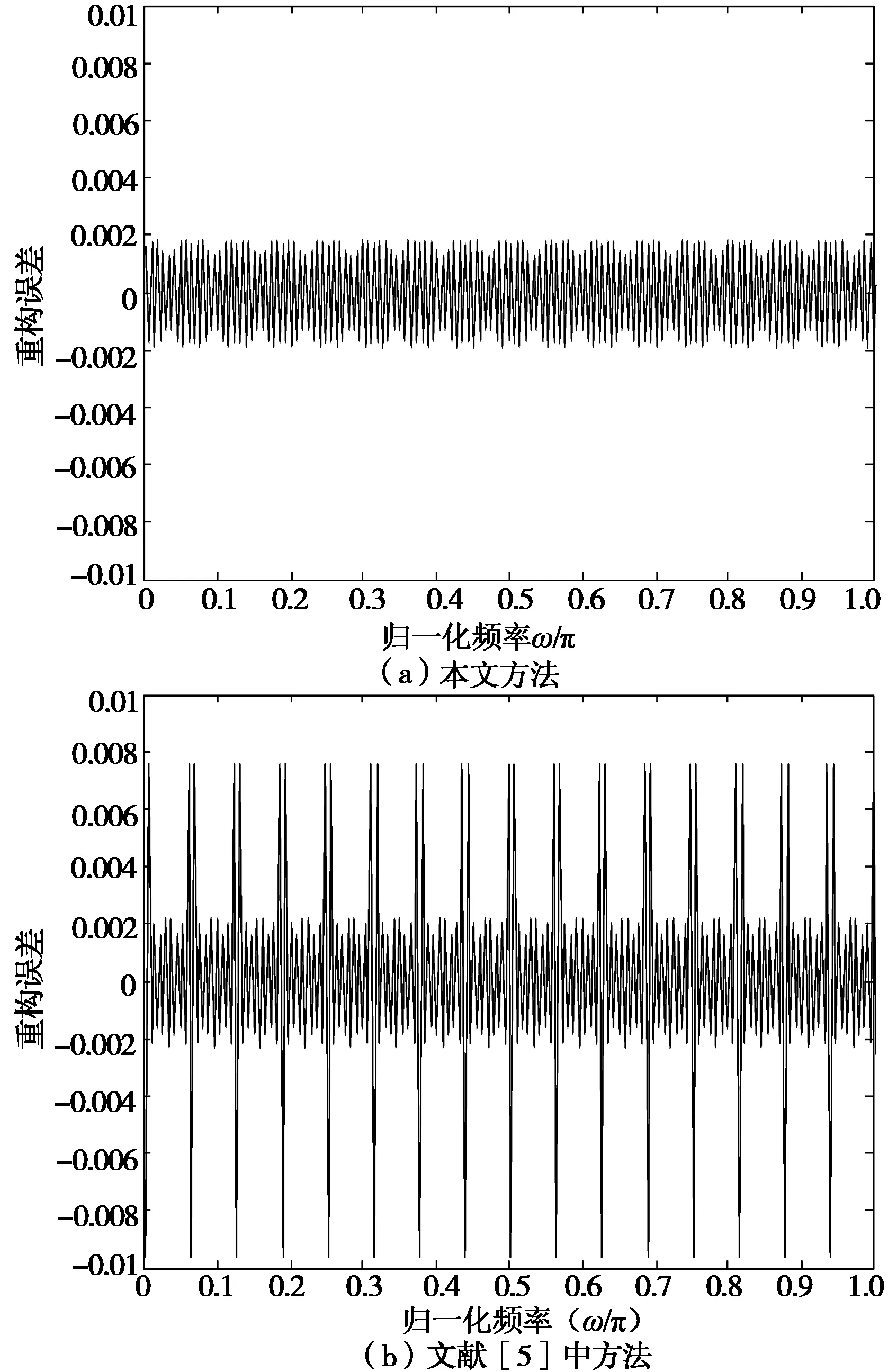
图3 余弦调制滤波器组的重构误差Fig.3 Reconstruction error of CMFBs

图4 128信道的余弦调制滤波器组Fig.4 128-Channel NPR CMFBs

5 结束语

本文研究了采用过渡带具有平方根余弦滚降特性的原型滤波器来设计NPR CMFBs的方法。这种原形滤波器采用了二阶锥规划算法进行最优化设计。与使用普通的原型滤波器相比,用这种方法设计NPR余弦调制滤波器组，能获得更小的重构误差和更大的阻带衰减。

参考文献：

[1] Cruz-Roldan F, Amo-Lopez P,Maldonado-Bascon S,et al. An efficient and simple method for designing prototype filters for cosine-modulated pseudo-QMF banks[J].IEEE Signal Process Letters,2002,9(1):29-31.

[2] Abu-Al-Saud W A,Studer G L.Efficient wideband channelizer for software radio systems using modulated pr filterbanks[J].IEEE Transactions on Signal Processing,2004,52(10):2807-2820.

[3] Bregovic R,Saramaki T. An efficient approach for designing nearly perfect-reconstruction low-delay cosine-modulated filter banks[C]//Proceedings of IEEE ISCAS.[S.l.]:IEEE，2002:825-828.

[4] Lu W S, Saramaki T,Bregovic R. Design of practically perfect-reconstruction cosine-modulated filter banks: A second-order cone programming approach[J].IEEE Transactions on Circuits and Systems,2004,51(3)：552-563.

[5] 李冰.软件无线电中的信道化技术研究[D].郑州:解放军信息工程大学，2007.

LI Bing. Research on Channelization Techniques for Software Defined Radio[D].Zhengzhou:The PLA Information Engineering University, 2007.(in Chinese)

[6] Chan S C，Yin S S.On the design of low delay nearly-PR and PR FIR cosine modulated filter banks having approximate cosine-rolloff transition band[C]//Proceedings of EUSIPCO.Hongkong: [s.n.],2004:1253-1256.

[7] Heller P N,Karp T,Nguyen T Q.A general formulation of modulated filter banks[J].IEEE Transactions on Signal Process,1999,47(4):986-1002.

[8] Yin S S,Chan S C,Tsui K M.On the design of nearly-PR and PR FIR cosine modulated filter banks having approximate cosine-rolloff transition band[J].IEEE Transactions on Circuits and Systems II,2008,55(6):571-575.

[9] Kumar A, Singh G K,Anand R S.An Improved Method for Designing Prototype Filter for M-Band Pseudo QMF Banks[J].IEEE Computer Society,2009:341-345.

[10] 鄢社锋，马远良.二阶锥规划方法对于时空域滤波器的优化设计与验证[J].中国科学E辑，2006,36(2):153-171.

YAN She-feng, MA Yuan-liang. Second-order cone programming method for optimal design and verification of time-space domain filter[J].Science In China Series E:Information Science, 2006,36(2):153-171.(in Chinese)

[11] Lu W S. Use SeDuMi to Solve LP,SDP and SCOP Problems: Remarks and Examples[EB/OL].(2007-01-29)[2009-12-23].http://menet.math.ecnu.edu.cn/lu/supplementary%20part/SeDuMi-Remarks.pdf.