利用IIR自适应频率估计器实现多频点估计*

(装备指挥技术学院 测控工程研究中心,北京 101416)

1 引 言

频率估计研究在通信系统中占有举足轻重的地位。传统的频率估计利用锁相环实现，由于数字锁相环是由模拟锁相环转变而来，设计参数存在经验值调整，难以建立起精确的数学模型。Lank[1-2]等人提出线性预测频率估计器，以及在此基础上加Kay[3]的线性预测频率估计器，其运算量小，易于实现，是对多普勒常用的估计方法，Griffiths[4]的自适应瞬时频率估计，梁国龙[5-6]单频信号自适应瞬时频率估计，算法简单，兼有可同时检测、窄带滤波、估计信号幅度、相位等优点，但诸方法频率估计器都只对单点频信号频率估计，应用范围受到限制。本文从IIR滤波器性能分析着手，使得IIR自适应频率估计多点频估计成为可能。

2 自适应滤波器原理及方差分析

2.1 二阶自适应滤波器

单点频信号估计一般采用二阶自适应滤波器。如图1所示，原始输入是信号s(k)和噪声n0(k)的混合波形，其中噪声与信号不相关；另一路参考输入是与信号不相关而与噪声相关的信号n1(k)。IIR滤波器的传递函数[7]为

(1)

式中，a=-2cosω，ρ1、ρ2为系统调节参数，ρ1可以直接实现对系统增益进行调整，ρ2为决定滤波器带宽的参数，0≤ρ1≤1，0≤ρ1<ρ2≤1。

图1 自适应滤波器模型结构Fig.1 Adaptive filter model structure

由图1可知，误差信号可通过式(2)求得：

e(k)=α(k)-β(k)

(2)

自适应算法的目的是通过调节参数a使得均方误差信号e2值达到最小。

E[e2]=E[α2]+E[β2]-2E[αβ]

(3)

由文献[8]可得到：

(4)

式中，Pss、Pnn和Psn分别为输入信号、参考信号和它们的相关功率谱。

(5)

(6)

式中，

与B*分别为A、B的共轭函数。

∮ρ1B*dz=∮ρ2A*dz

(8a)

由0≤ρ1<ρ2≤1可得:

(9)

从式(9)可以看出，方程无条件存在极值。图2为H(z)、a与ρ2的关系，从图中可以看出，ρ2越接近单位圆，传递函数波谷越陡。

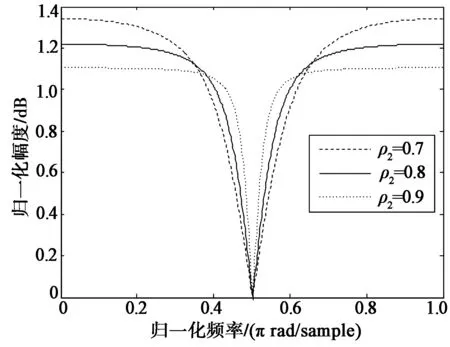
图2 二阶滤波器幅频响应(f=0.5，ρ1=1)Fig.2 Amplitude-frequency responses of second order filter(f=0.5，ρ1=1)

2.2 高阶自适应滤波器

多点频信号估计必须采用高阶自适应滤波器。通过对双通道自适应滤波器性能分析可以有效推导高阶自适应滤波器的特性。双通道滤波器的传递函数为

式中，a1=-2cosω1，a2=-2cosω2，k0=k4=1，k1=k3=a1+a2，k2=a1a2+2。

则通过自适应滤波后可求得:

式中，C1、C1分别为两个信号的幅度，Pn1n1、Pn2n2分别为两个通道引入的噪声功率，Pn1n2为输入信道相关功率谱。可求得:

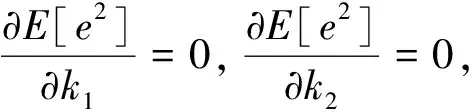
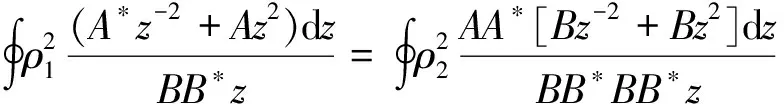
(13)

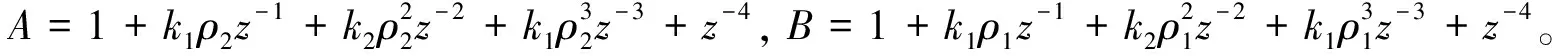
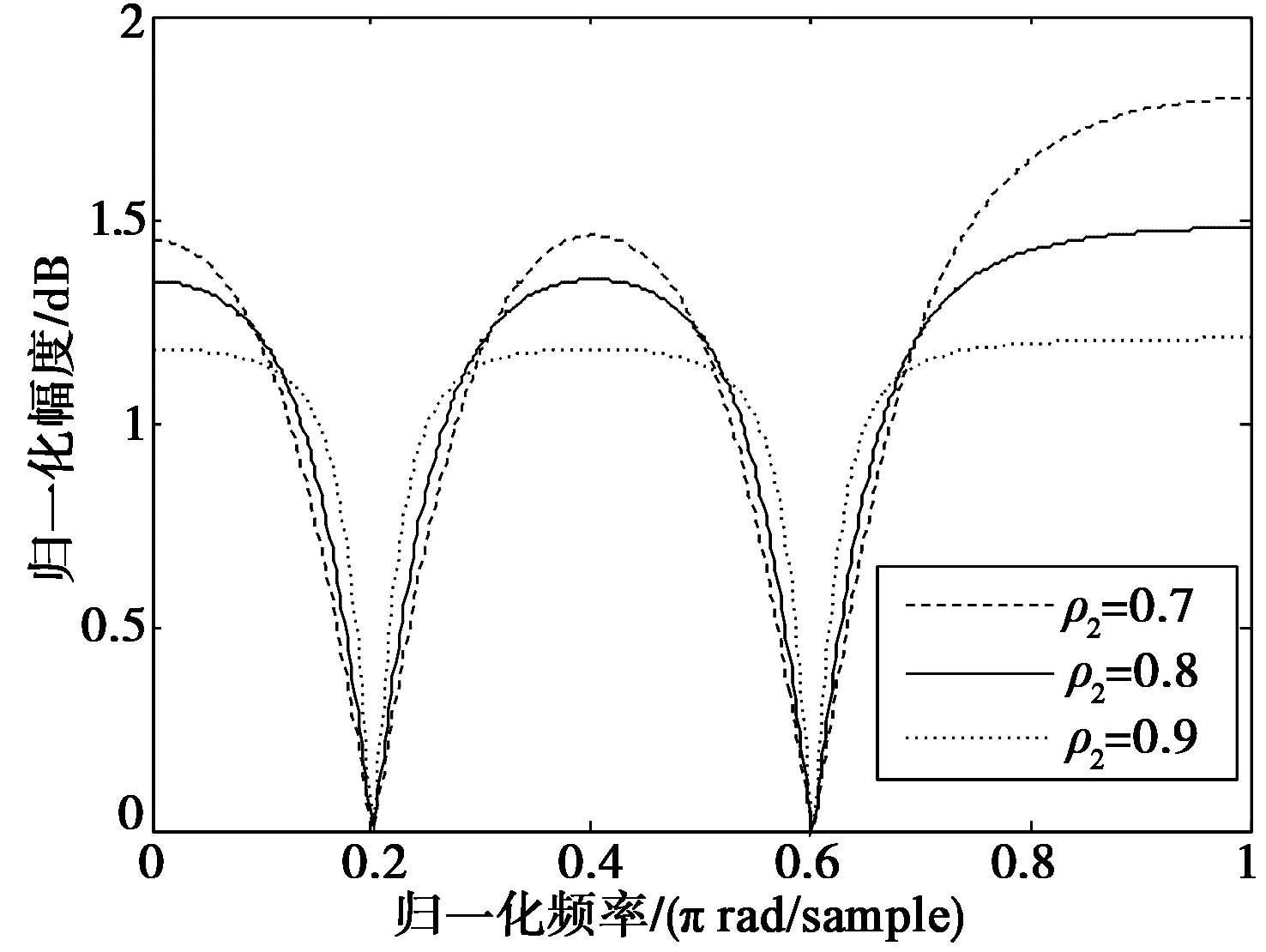
图3 高阶滤波幅频响应(f1=0.2，f2=0.6，ρ1=1)Fig.3 Amplitude-frequency responses of high order filter(f1=0.2，f2=0.6，ρ1=1)

与二阶自适应滤波器系统响应相比，对于k1、k2来说，式(13)并非为线性变化，均方差存在局部最大值。图4为方差与参数d1、d2之间的关系，从图中可以看出，当-4≤d1≤4与-4≤d2≤4时，方差呈现出单峰特性，自适应滤波器趋于收敛，然而在区域外存在许多局部最小点。可以得出结论：高阶自适应滤波器只有当信号载波频率与窄带过程中心频率相差控制在适当范围内，滤波器才能实现收敛。因此对多频点频率跟踪时，需要利用FFT对信号进行初始值估计。在此对FFT特性不再赘述。

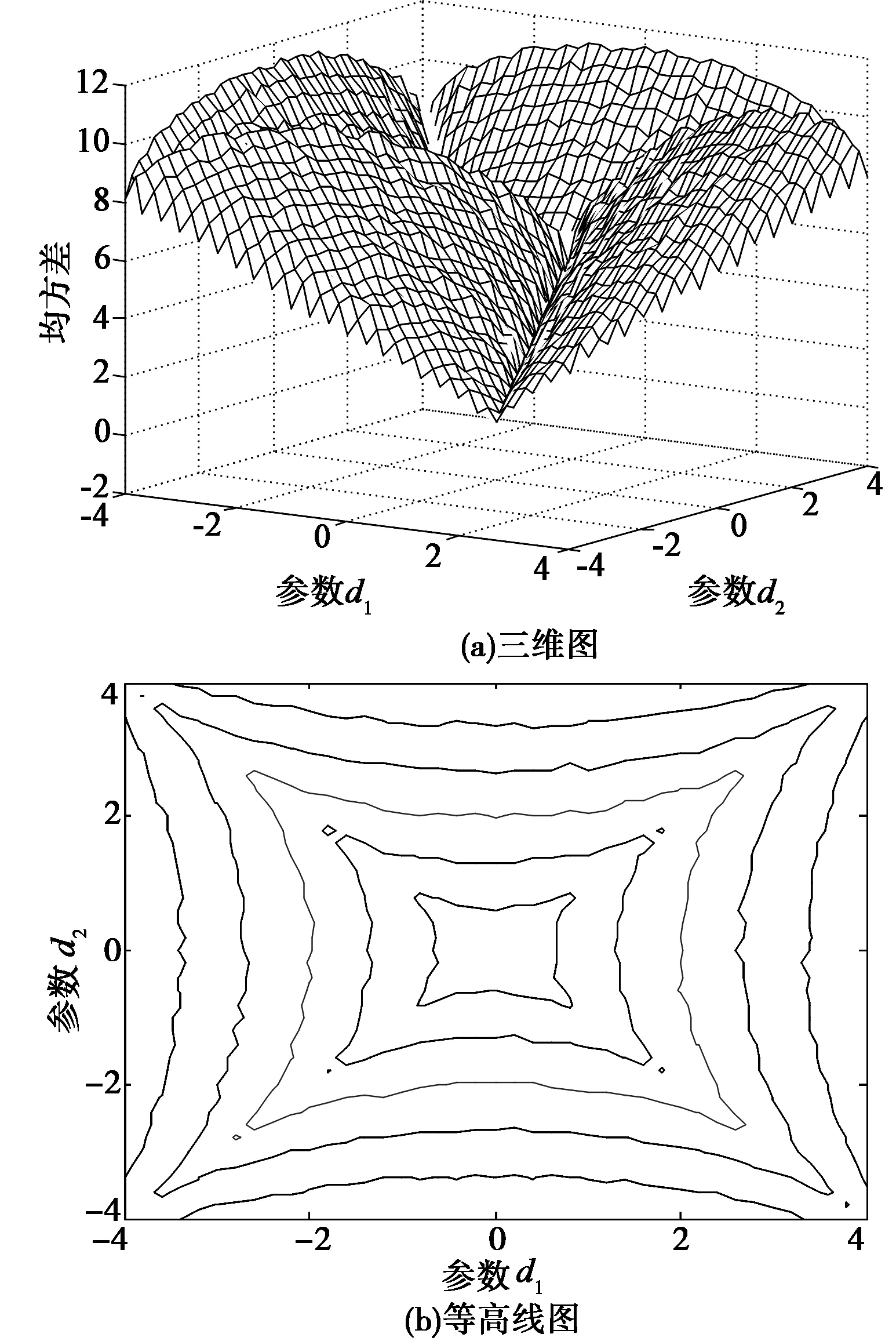
图4 参数d1、d2对自适应滤波器均方差的影响Fig.4 The effect of parameters d1，d2 on mean square of adaptive filter

3 抽头权向量的时间更新

算法中抽头权向量[9]新使用了变步长μ设计，令

则可以求得:

(14a)

误差信号为

(15)

该算法的滤波器参数更新如下：

w(k)=w(k-1)-μ(k)e(k)

(16)

目标是保证当算法远离最优值的时候步长μ(k)要足够大，而当算法逐渐接近最优值的时候μ(k)要逐渐减小。本文通过建立中间变量φ(k)对μ(k)进行控制：

φ(k)=γφ(k-1)+(1-γ)α(k)α(k-1)

(17)

式中，γ为指数权参数控制滤波器估计质量。在自适应最初阶段，φ(k)的估计值很大，产生很大的μ(k)；当自适应过程接近最优值时，输出信号接近零，产生较小μ(k)，通过调整可以加快收敛速度。

步长的更新公式为

μ(k)=μ(k-1)+φ(k-1)

(18)

在干扰不变时，前一次输出信号包含了自适应变化信息，使自适应参数逐渐向最优值靠近。

4 仿真与结果分析

性能仿真中主要采用双点频信号及三点频信号进行频率估计。图5为载噪比10 dB-Hz的多点频信号进行频率跟踪，滤波器的初始频率由FFT估计得到。随着频点自跟踪的进行，频率估计偏差减小，表明频点自跟踪的过程是向着频率估计优化的方向进行的，而且是收敛的。

图6为IIR自适应滤波器与传统锁相环跟踪性能比较。参数如下:信号长度为1 s，载波频率为100 Hz，采样率为24 kHz，白噪声，稳态时自适应滤波器与锁相环带宽同时调整为1 Hz和3 Hz。选取滤波的稳态部分估计频率，在每个载噪比下选取500个样本作频率估计。仿真结果表明，在FFT频率辅助下IIR自适应滤波器可以实现多频点信号频率估计；在不同带宽条件下IIR自适应滤波器拥有与锁相环相近的跟踪精度，当等效噪声带宽为1 Hz，频率估计误差小于0.1 Hz。

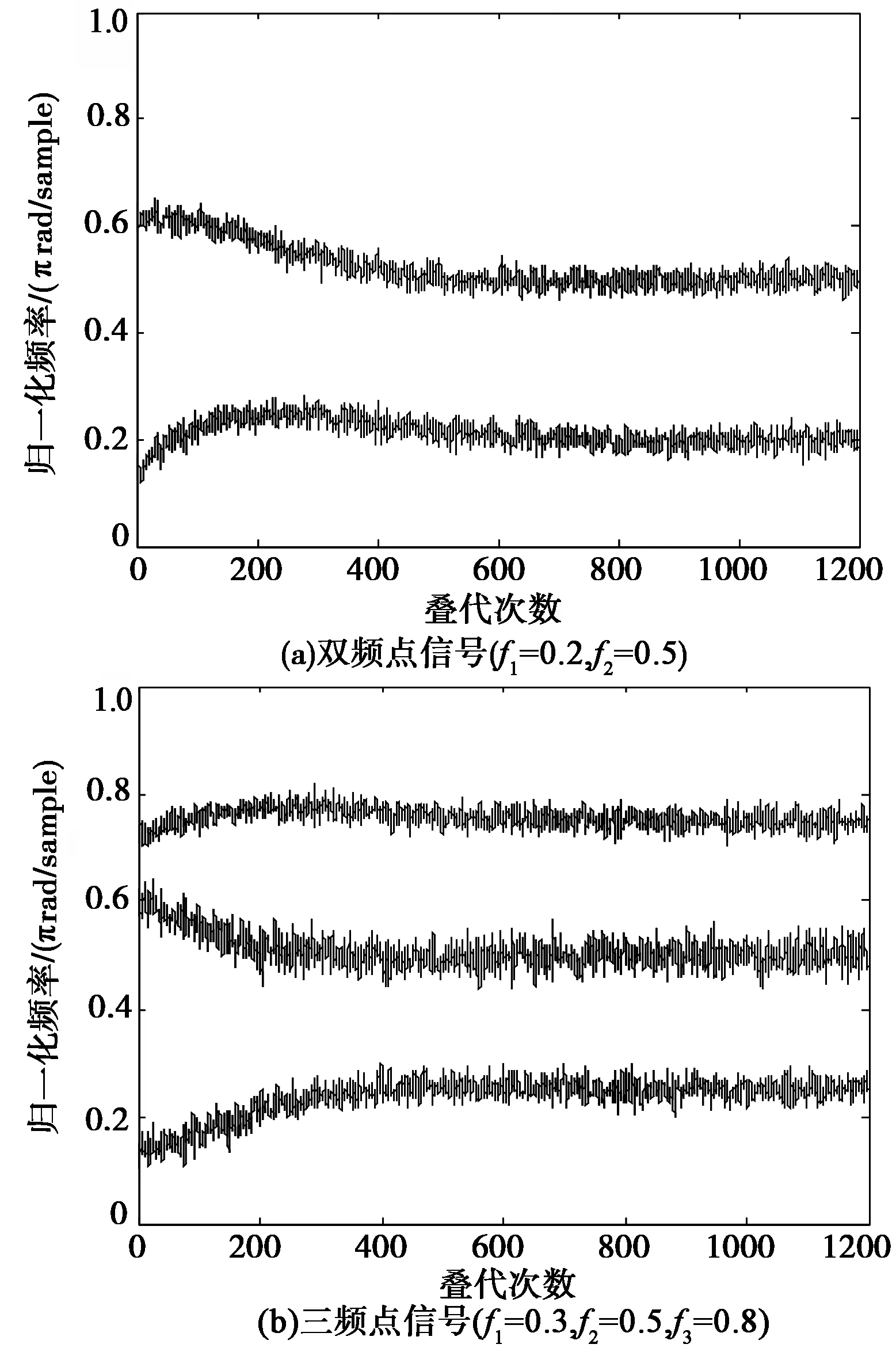
图5 对多频点信号参数估计曲线Fig.5 Estimation plot for multi-frequency signal

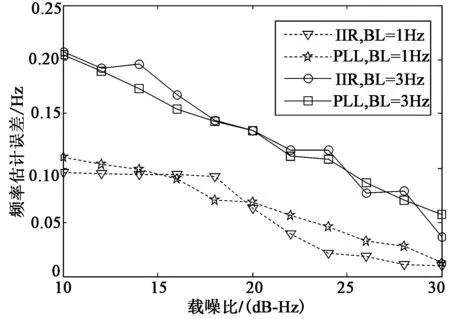
图6 不同载噪比下IIR与PLL跟踪频率误差比较Fig.6 Comparison of the frequency tracking error between IIR and PLL with different CNR

5 结束语

IIR自适应频率估计器的优点是具有窄带滤波的作用，当通带较窄时，能够获得较大处理增益，然而估计器的性能受传递函数影响较大。本文通过分析二阶及四阶IIR滤波器均方差对自适应的影响，证明了二阶IIR模型具有单峰特性，能够实现稳定收敛；而高阶IIR模型具有多态性，因此需要对估计参数进行初始化。在此基础上,提出利用FFT频率估计辅助IIR自适应滤波器实现多点频频率估计，为多点频频率估计的自适应过程的参数选取提供了理论依据，较传统的锁相环算法，IIR自适应频率估计器具有不产生混频分量、能够实现全频段频率估计的优点。该设计方案在直扩/跳频混合扩频测控中对多点频率估计值的提取具有一定的指导意义。

参考文献：

[1] Pradhan A K.Power System Frequency Estimation Using Least Mean Square Technique[J].IEEE Transactions on Power Delivery,2005,20(3):1812-1816.

[2] Lank G W,Reed I S,Pollon G E.A semi coherent detection and Doppler estimation statistic[J].IEEE Transactions on Aerospace and Electronic Systems,1973,AES-9(2):151-165.

[3] Kay S M.A fast and accurate single frequency estimator[J]．IEEE Transactions on Acoustics,Speech and Signal Processing, 1989,37(12):1987-1990.

[4] Griffiths L J.Rapid measurement of digital instantaneous frequency[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1975,23(2):207-222．

[5] 梁国龙．回波信号瞬时参数序列分析及其应用研究[D].哈尔滨：哈尔滨工业大学,1997.

LIANG Guo-long．A study on Instantaneous Parameter Sequence Analysis of Echoes and its Application[D]．Harbin: Harbin Engineering University,1997.(in Chinese)

[6] 梁国龙,杨春,王德俊.频点自跟踪自适应频率估计器性能研究[J].电子学报,2005,33(7):1204-1208.

LIANG Guo-long，YANG Chun，WANG De-jun. Research on Properties of Frequency Auto-Tracking Adaptive Frequency Estimator[J].Acta Electronica Sinica,2005,33(7):1204-1208.(in Chinese)

[7] 胡广书．数字信号处理[M].北京：清华大学出版社,2006:78-80.

HU Guang-shu.Digital Signal Processing[M].Beijing: Publishing House of Tsinghua University,2006:78-80. (in Chinese)

[8] Corinthios M J. Complex-variable distribution theory forLaplace and z transforms[J].IEEE Transactions on Image Signal Processing,2005,52(1):97-106.

[9] Aboulnasr T,Mayyas K.A robust variable step-size LMS-type algorithm: analysis and simulation[J].IEEE Transactions on Signal Processing,1997,45(3):631-639.