基于遗传算法的星载InSAR多基线编队构形优化设计*

李 洁1,黄海风,梁甸农

(1.海军装备研究院，北京 100161;2.国防科技大学 电子科学与工程学院，长沙 410073)

1 引 言

分布式星载干涉合成孔径雷达(InSAR)测高系统是将卫星编队和星载SAR技术相结合形成的新体制雷达系统[1-2]，它利用编队卫星构成的空间基线进行干涉测高，具有测高精度高、生存力强、周期短、成本低等优点。它的多星编队模式能够形成多个干涉通道，是实现多基线定位与测高的重要前提。本文以此为背景，研究了多基线编队构形的优化设计问题。

卫星的编队构形决定了空间基线的长度和指向角，而基线直接关系到干涉测高中参数的误差传播系数，因此，编队构形设计是实现高精度测高任务的一个非常重要的环节。实现此类任务的编队构形设计，一方面需要符合编队运动模型，另一方面需要满足干涉测高的功能要求。目前，国内外很多文献提出若干卫星相对运动模型描述编队构形中的运动规律。理论上讲，分布式SAR系统可以根据需要设计任意形状的编队，但在实际中由于很多构形需要消耗大量燃料而很难实现[3]。文献[4]推导了被动稳定的编队轨道飞行要素的解析解，提出了一种适用于分布式SAR特点的编队构形设计方法。干涉车轮、干涉钟摆等典型构形亦是基于Hill方程、消耗燃料少、从传统正侧视几何出发分析基线稳定性得到的。文献[5]基于单基线测高精度模型设计编队构形。文献[6]设计了干涉基线长度相等的编队构形，解决了空间立体编队中基线耦合的问题，兼具高程测量和地面运动目标检测两种功能。另外，还有一些分布式星载InSAR编队设计是建立在典型构形上，例如Cartwheel、星下点圆形构形、空间圆形构形等[7～9]。本文采用遗传算法(GA)对星载InSAR系统的多基线编队进行优化设计，直接以编队卫星的6个轨道根数为设计变量，同时考虑卫星飞行安全因素和去相关因素的影响，以三星编队的分布式InSAR提供系统的多基线为背景，以提高测高精度为优化目标对多基线优化问题进行讨论。首先从多基线定位方程出发推导了测高精度公式并建立了多基线测高精度模型，然后分析并推导了编队构形需要考虑的约束条件，最后根据约束条件利用遗传算法搜索得到较好的三星编队构形。

2 目标函数

分布式卫星系统具有多种任务功能。优化模型的目标函数应根据分布式卫星系统的任务功能以及系统顶层设计的性能指标要求来选取，用性能指标的加权和来表示：

(1)

式中,km是性能指标σm的加权系数。

分布式星载InSAR系统实现干涉测高任务，顶层设计要求较高的测高精度，因此，本节以多基线高程误差σh为性能指标优化编队。构造如下目标函数：

J=khσh-1

(2)

J越大，表示各性能指标越高，而σh越大表示测高误差越大，因此改为σh-1。

3 多基线测高误差方程

建立如图1所示的地心固连坐标系XYZ。其中，O为坐标原点。S为既发射信号又接收信号的主星，S1和S2为编队小卫星群中两颗只接收信号的辅星。主图像成像慢时刻t，主星位置矢量用RS表示；两幅辅图像成像慢时刻t1、t2，辅星位置矢量分别用RS1和RS2表示。B1和B2分别表示主星和两辅星间的基线。T为待求的点目标，它在地球表面的位置用RT表示。

图1 三星编队分布式InSAR成像几何模型Fig.1 The geometrical imaging model of InSAR system

根据干涉测高基本原理，分别列出点目标的距离方程和多普勒方程：

|RS-RT|=r

(3)

(4)

主图像和辅图像1、辅图像2分别干涉形成两个干涉通道，Δφ1、Δφ2分别表示目标在两个干涉通道中的干涉相位。根据干涉测量的原理，列出干涉相位方程如下：

(5)

(6)

联立式(3)、(4)、(5)、(6)，即可求出目标三维坐标。根据式(7)即可求出目标的绝对高程：

h=|RT|-Re

(7)

式中,Re为当地水准面地心距。

每个参数的误差乘以各自的误差传播系数后成为测高总误差σh的一部分。将式(3)～式(6)对各参数求偏导可计算出参数与定位解之间的误差传播系数，进而推导出高程误差传播系数[15]。

假设各参数测量误差之间统计独立，则测高总误差表达式为

(8)

4 约束条件

基线的设计必须考虑以下几个约束[11]：

(1)任意两颗卫星的距离小于临界基线，保证回波的相干性；

(2)防止卫星碰撞，确保编队飞行安全；

(3)限制垂直基线长度，满足测高精度的要求。

其中,第二条约束牵涉到卫星动力学的诸多理论知识和轨道控制的丰富的实践经验。文献[12]在分析了地球扁率、大气等摄动因素后，指出应当以一定的交轨迹基线保证编队的安全性。具体办法是，设计编队卫星的a、i、ω相同，而e、Ω、f略有不同。构形在垂直于飞行方向的平面内的投影是一个以aΔΩ、aΔe为长短半轴的椭圆，长度至少大于150 m。沿航向基线长度由Δf确定，以2aΔe振幅振荡。另外，aΔΩ、aΔe的上限还受到垂直基线去相关的限制，主要表现在受垂直于轨道面的基线长度Bc(Cross-track Baseline)和卫星到地心连线方向基线长度Bv(Vertical Baseline)的约束。

4.1 轨道根数与Bc、Bv的关系

在相对运动坐标系中，Bc为伴随卫星位置z方向的分量，Bv为x方向的分量。假设s表示参考卫星，c表示伴随卫星，(x,y,z)T为伴随卫星的坐标。令

由相对运动方程可以得到[13]：

(9)

根据二体运动模型可知[13]：

式中,Δe=es-ec,Δf=fs-fc。将式(10)代入式(9)，不考虑f和i的影响，则有：

(11)

(12)

4.2 距离向相关系数对Bc、Bv的约束

不考虑配准误差，那么距离向相关系数与垂直于轨道面的基线长度Bc和卫星到地心连线方向基线长度Bv的关系分别为[14]

(13)

(14)

式中,θ为下视角，r为目标到辅星的距离，Br为发射信号带宽，βr为距离向地面坡度。为了得到较好的测高性能，令{ρc,ρr}≥0.9，根据式(13)、(14),即可得到Bc和Bv的临界基线Bcc、Bvc。综合式(11)、(12)，即可计算出aΔΩ、aΔe的上限。

5 遗传算法与仿真实验

遗传算法是一种通过模拟自然进化过程搜索最优解的方法，具有解决复杂的全局优化问题的能力。结合目标函数和优化条件，以卫星的轨道根数xi=(ai,ei,ii,Ωi,ωi,fi)为设计变量，X=(x1,x2,…xn)为决策变量，求解带约束的目标函数J。

设定参数进行仿真分析。给定主星的轨道根数和雷达参数(如表1所示)。根据式(13)、(14)，结合条件{ρc,ρr}≥0.9可以得到Bcc、Bvc约为1 100 m，方位向临界基线约为800 m。根据式(11)、(12)计算可得a0Δe、a0ΔΩ的上限为1 500。高程误差σh根据式(8)计算得到，各参数的误差取为合理的常数：σr=1.5 m，σfdc=0 Hz，σB=0.01 m，σRs=1 m，σVs=0.01 m/s。由于基线的方向变化使距离向去相关和方位向去相关分别变化，因此,σφ是随着基线姿态变化的，并非一个固定值。σφ根据两个通道信号相干系数来计算[10]。

表1 仿真参数Table1 Simulation parameters

综合上述约束条件，遗传算法优化模型为

(15)

式中，下标i为辅星的编号，0表示主星。

操作的具体过程如下：

(1)设置遗传算法参数。种群规模设为30，交叉概率为0.4，变异概率为0.05；

(2)初始化种群。在各设计变量约束范围内选取服从均匀分布的随机变量组成30个决策变量(初始种群)，决策变量即为遗传算法中的染色体；

(3)对染色体依概率进行交叉和变异操作；

(4)计算所有染色体的目标函数J，并设定门限值，将目标函数值大于门限值的染色体保存在次最优解的集合中；

(5)计算次最优解集合中染色体的目标函数值；

(6)通过旋转赌轮选择染色体。将次最优解集合中所有染色体的目标函数值相加求和，然后产生一个在0与总和之间的随机数m。从次最优解集合中编号为1的染色体开始，将其目标函数值与后继染色体的目标函数值相加，直到累加和大于等于m，最后加进去的即为要选择的染色体；

(7)重复步骤3～6，直到满足终止条件；

(8)从最优解集合中选取染色体作为最优解。

采用遗传算法求解多基线编队构形优化问题的基本流程如图2所示。

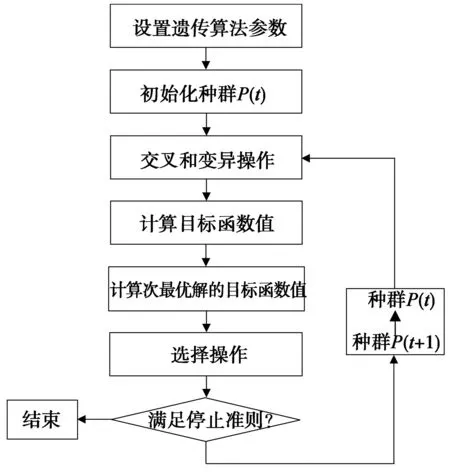
图2 遗传算法基本流程Fig.2 The basic flow of GA

设繁殖迭代500次，根据式(15)搜索得到优化编队，轨道根数如表2所示。表3列出优化后编队各参数的误差传播系数。为方便比较，表3亦同时给出经简单优化的三星编队和两星编队的误差传播系数[15]。经过比较可以看出：多基线的误差传播系数小于单基线的误差传播系数；经本文算法优化后，多基线的某些较大误差传播系数变小，高程误差变小。可以得出以下结论：多基线系统提供的冗余信息可以提高测高精度；本文的算法优于文献[15]中简单的以基线指向角为优化变量的优化算法。

表2 优化编队参数Table 2 Optimization formation parameters

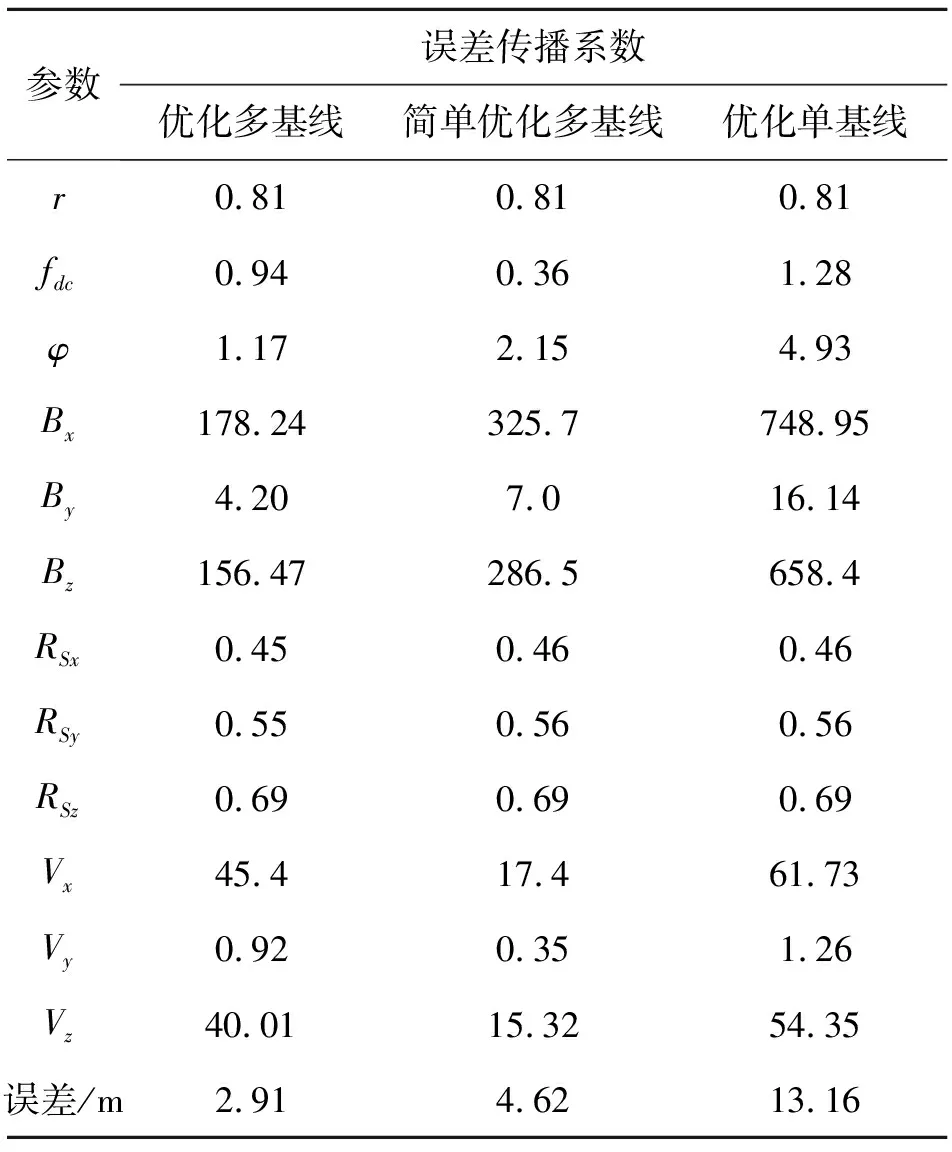
表3 误差传播系数对比Table 3 Error coefficient contrast

6 结束语

本文采用遗传算法基于多基线测高精度模型对分布式星载InSAR多基线测高系统的编队构形进行优化，将多基线高程误差的倒数作为优化问题的目标函数。从相对运动模型出发综合卫星飞行安全、信号相干性等因素推导了设计变量的约束条件，至此建立了完整的优化问题。采用遗传算法进行求解，并进行了仿真实验。此种编队构形优化方法没有基于任何编队构形的假设，具有通用性，仿真实验证明了优化方法的正确性。

参考文献：

[1] Gerhard Krieger,Hauke Fiedler,Alberto Moreira.Bi- and Multistatic SAR:Potentials and Challenges[C ]//Proceedings of EUSAR. Germany:[s.n.],2004:365-370.

[2] Hanle E.Survey of bistatic and multistatic radar [J].IEE Proceedings,1986,133(7):587-595.

[3] 林来兴.小卫星编队飞行及其轨道构成[J].中国空间科学技术,2001(2):23-28.

LIN Lai-xing.Formation Flying of Small Satellite and Its Orbital Configuration[J].Chinese Space Science and Technology,2001(2):23-28.(in Chinese)

[4] 陈杰，周荫清，李春升.分布式SAR小卫星编队轨道设计方法研究[J].中国科学E辑信息科学，2004，34(6):654-662.

CHEN Jie,ZHOU Yin-qing,LI Chun-sheng.Design of Distributed SAR satellites Formation Orbit[J].Science in China,Ser.E，2004，34(6):654-662.(in Chinese)

[5] 郝继刚，张育林.SAR干涉测高分布式小卫星编队构形优化设计[J].宇航学报,2006,27(4):654-658.

HAO Ji-gang,ZHANG Yu-lin.Formation Optimized Design for the Height Measurement of InSAR Using Distributed Micro-Satellites[J].Journal of Astronautics,2006,27(4):654-658.(in Chinese)

[6] 李真芳，王彤，保铮，等.同时地形高程测量和地面运动目标检测的分布式InSAR最优编队构形[J].宇航学报,2004,25(6):642-648.

LI Zhen-fang,WANG Tong,BAO Zheng,et al.The optimal formation configurations for both GMTI and DEM using distributed satellites InSAR[J].Journal of Astronautics,2004,25(6):642-648.(in Chinese)

[7] Fiedler H,Loffeld G,Nies H,et al. Analysis of Bistatic Configurations for Spaceborne SAR Interferometry[C ]//Proceedings of EUSAR 2002.Cologne,Germany:[s.n.],2000:29-32.

[8] Krieger G,Wendler M.Comparison of the Interferometric Performance for Spaceborne Parasitic SAR Configurations[C ]//EUSAR 2002.Berlin:VDE VERLAGGMBH,2002:467-470.

[9] Burns R,McLaughlin C A,Leitner J,et al.TechSat21: formation design, control, and simulation[J].IEEE Aerospace Conference Proceedings,2000(7):19-25.

[10] 黄海风，朱炬波，梁甸农.主星带辅星编队干涉SAR编队设计约束条件分析[J].中国空间科学技术，2006，26(3):20-26.

HUANG Hai-feng,ZHU Ju-bo,LIANG Dian-nong.Restriction of Spaceborne Multistatic InSAR Formation Configuration Design[J].Chinese Space Science and Technology，2006，26(3):20-26.(in Chinese)

[11] 杨凤凤，黄海风，梁甸农.基于遗传算法的分布式星载SAR-GMTI编队优化[J].电子学报，2006，35(6):1037-1041.

YANG Feng-feng,HUANG Hai-feng,LIANG Dian-nong.GMTI Mode Formation Optimization for Distributed Satellites SAR System[J].Acta Electronica Sinica,2006，35(6):1037-1041.(in Chinese)

[12] Samone D Amico,Oliver Montenbruck,Christian Arbinger,et al. Formation flying concept for close remote sensing satellites[C]//Proceedings of the 15th AAS/AIAA Space Flight Mechanics Conference.Colorado:AAS,2005:23-27.

[13] 郗晓宁,王威,等.近地航天器轨道基础[M].长沙:国防科技大学出版社,2003：262-267.

XI Xiao-ning,WANG Wei,et al.Near Earth Orbit Aerospace Foundation[M].Changsha:National University of Defense Technology Press,2003：262-267.(in Chinese)

[14] 孙造宇，梁甸农，董臻.星载分布式SAR干涉信号分析[J].信号处理，2007，23(2):245-249.

SUN Zao-yu,LIANG Dian-nong,DONG Zhen.Interferometric Signal Analysis of Spaceborne Distributed SAR System[J].Signal Processing,2007，23(2):245-249.(in Chinese)

[15] 李洁，黄海风，梁甸农.基于定位方程的多基线星载InSAR测高精度分析[J].雷达科学与技术，2009,7(3):194-199.

LI Jie,HUANG Hai-feng,LIANG Dian-nong.Height-Measurement Accuracy Analysis of Multi-Baseline Spaceborne InSAR System Based on Location Equations[J].Radar Science and Technology，2009,7(3):194-199.(in Chinese)