球-圆柱滚子组合转盘轴承承载能力的计算

汪 洪，陈 原

(1.洛阳LYC轴承有限公司，河南 洛阳 471039；2.洛阳轴研科技股份有限公司，河南 洛阳 471039)

1 前言

球-圆柱滚子组合转盘轴承的典型结构如图1所示，其主要适用于承受较大轴向载荷，同时倾覆力矩很小且回转半径较大的场合。与同尺寸的三排滚子转盘轴承相比，其轴向承载能力基本相同，但轴向的尺寸更小，结构更为紧凑，因此具有更好的综合经济性。由于滚动体与滚道间同时存在点接触和线接触，给此类轴承的分析计算带来很大的困难。文献[1]介绍的转盘轴承的分析方法仅适用于单一接触形式的转盘轴承。对于混合接触形式转盘轴承的分析，该方法无法适用。这里重点研究运用计算机数值算法，对混合接触形式转盘轴承滚动体载荷的求解和对其动、静承载能力曲线的绘制。

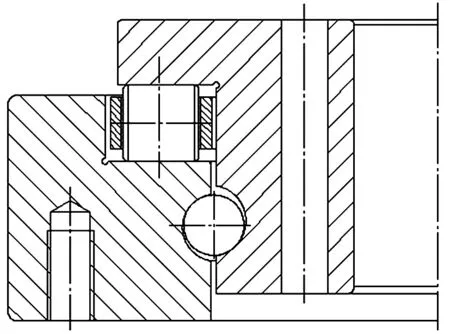
图1 典型球-圆柱滚子组合转盘轴承结构

2 滚动体载荷分布的计算方法

2.1 滚动体载荷与弹性接触变形间的关系

由文献[1]可知，滚动体承受的载荷及其弹性变形量间的关系为：

对于滚子接触，Q=K1δ1.1

(1)

对于钢球接触，Q=K2δ1.5

(2)

式中：K1,K2分别为变形常数，仅取决于轴承的结构参数和材料。

2.2 单排滚动体的合力及合力矩的计算

为简化计算，假设轴承的套圈均为刚体，滚动体与套圈间不存在间隙。设定如下符号:Z1为主滚道滚子的数量；Z2为辅滚道钢球的数量；Dw1,Dw2分别为滚子和钢球直径；Dpw1,Dpw2分别为滚子组和球组节圆直径；ε1,ε2分别为主、辅滚道的载荷分布参数；Qmax1,Qmax2分别为主、辅滚道滚动体承受的最大轴向载荷。设套圈在轴向载荷和倾覆力矩的作用下的轴向位移为δa，倾角为θ，则主、辅滚道的载荷分布参数分别为：

(3)

由以上两式得：

(4)

主滚道所有滚子轴向力的合力F1为[1]:

F1=Qmax1Z1Jo(ε1)

(5)

主滚道所有滚子合成的力矩M1为：

M1=0.5Qmax1Z1Dpw1Jm(ε1)

(6)

cosφ1dφ1。

同理，辅滚道上所有钢球轴向力的合力F2为:

F2=Qmax2Z2Jo(ε2)

(7)

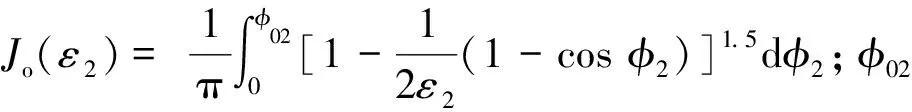
辅滚道上所有钢球合成的力矩M2为：

M2=0.5Qmax2Z2Dpw2Jm(ε2)

(8)

cosφ2dφ2。

因此，当已知单排滚动体的最大载荷和载荷分布参数时，即可求出单排滚动体的轴向合力和合力矩。

2.3 两排滚动体载荷分布的计算

设主、辅滚道滚动体的最大轴向压缩量为δmax1,δmax2，根据文献[1]有：

δmax1=ε1θDpw1；δmax2=ε2θDpw2。

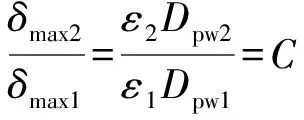
(9)

由(1)式和(2)式得：

将其代入(9)式得：

(10)

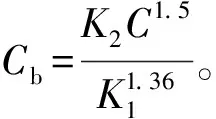
根据力平衡关系得：

Fa=F1-F2

(11)

根据力矩的平衡关系得：

M=M1+M2

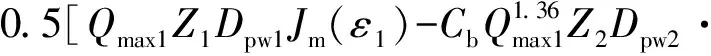
Jm(ε2)]

(12)

(11)式和(12)式构成了求解球-圆柱滚子组合转盘轴承载荷分布的基本方程组。由(3)式可知ε2是ε1的函数。因此，当轴承的外部载荷Fa和力矩M己知时，此方程组是关于ε1和Qmax1的二元非线性方程组。为便于求解，可利用变量消元法消去方程中的Qmax1项，使其变成关于ε1的一元非线性方程，然后利用Newton迭代法求出ε1值，进而求出每排滚动体的载荷分布。

3 接触强度的计算和静承载曲线的绘制

3.1 接触强度的计算

当转盘轴承的外载荷已知时，运用上述滚动体载荷的计算方法，可以求出作用于滚子上的最大载荷Qmax1。根据Hertz接触理论，圆柱滚子的最大接触应力σmax为：

(13)

式中:Lwe为滚子的有效接触长度。

3.2 静承载能力曲线的绘制方法

静承载能力曲线是转盘轴承选型的重要依据。转盘轴承受到的径向力相对较小，绘制静承载曲线时，仅考虑轴向力和倾覆力矩。取安全系数fs=1，则静承载曲线上每一点对应的载荷应恰好使σmax=[σmax]。球-圆柱滚子组合转盘轴承的结构特点决定了它主要承受轴向力，不能承受大的倾覆力矩和径向力。因此在静承载曲线上必须对轴向载荷的偏心量e作出如下限制:

对e的限制在静承载能力曲线上表现为通过坐标原点的直线段。

当σmax达到[σmax]时，作用在滚子上的载荷即为滚子的最大许用载荷。由(13)式得到滚子的最大许用载荷Fm为:

在(11)式和(12)式中，令Qmax1=Fm,则构成了主推力滚道以ε1为参数的静承载能力曲线的参数方程:

(14)

Jm(ε2)]

(15)

当轴承同时承受较大的倾覆力矩和小的轴向力时，辅滚道上最大接触应力将先于主推力滚道达到其许用接触应力。因此，应同时构造辅滚道的静承载能力曲线，并求出与主滚道承载曲线的交点坐标，最终形成折线形式的完整的静承载曲线。121.36.4000球-圆柱滚子组合转盘轴承的静承载曲线如图2所示。

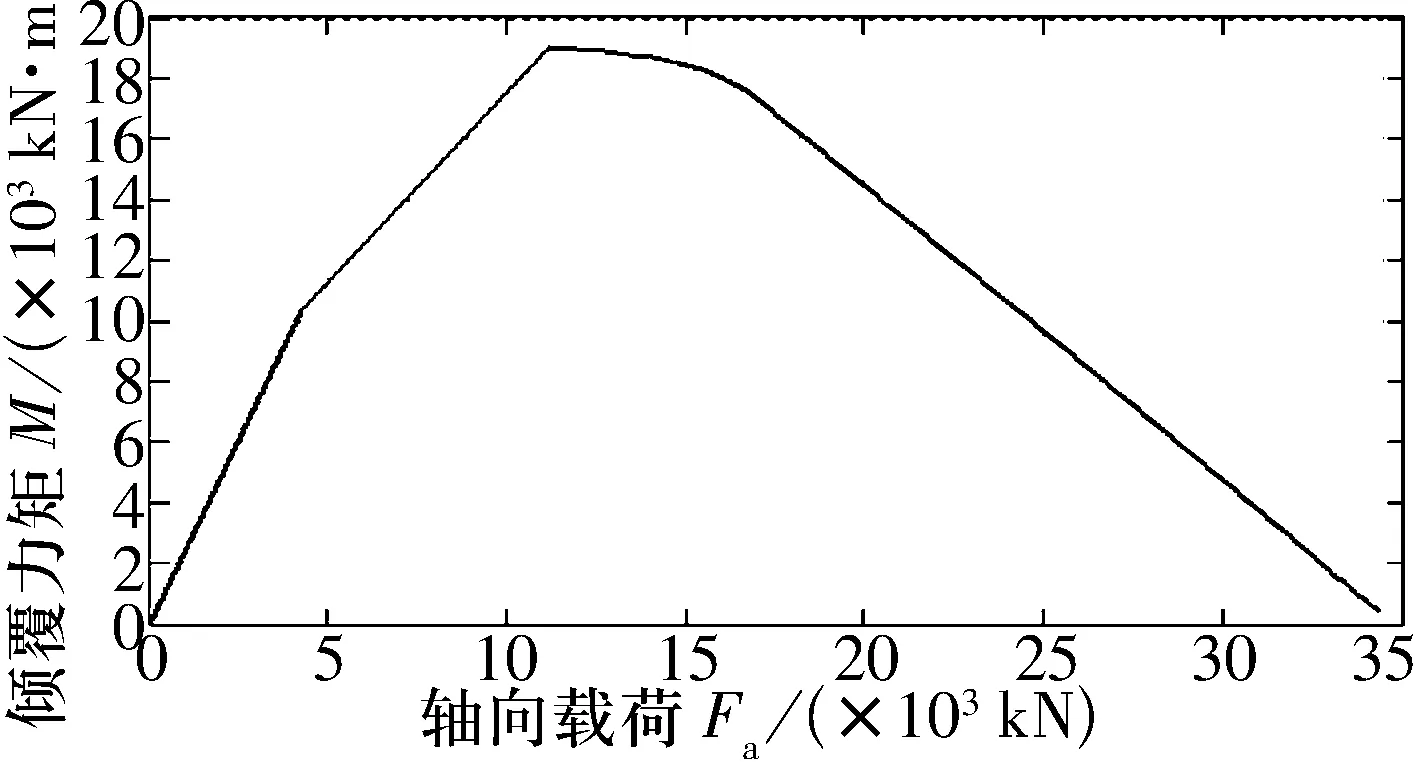
图2 静承载能力曲线

4 工作寿命的估算和动承载曲线的绘制

这里，以Lundberg-Palmgren的疲劳寿命理论为基础，研究其寿命的计算。

接触角为90°的滚子轴承的额定滚动体载荷Qc为[2]:

式中:B为常数。球轴承的额定滚动体载荷与滚子轴承类似，此处不再赘述。

当外载荷己知时，按照上述滚动体载荷分布的计算方法，可求出作用于每个滚道的载荷分布函数:

式中:n为系数，点接触n=1.5,线接触n=1.1。

对于旋转的滚道，其当量滚动体载荷Qe1为:

对于静止的滚道，其当量滚动体载荷Qe2为:

单个滚道的基本额定寿命L10为：

式中：点接触ε=3，线接触ε=4。

对于轴承的每个滚道，其使用概率和使用寿命之间存在如下关系:

由于滚道的疲劳破坏是彼此独立的事件，根据乘法规则，整套轴承的使用概率Sb等于各个滚道使用概率之积，即Sb=Se1Se2Si1Si2。

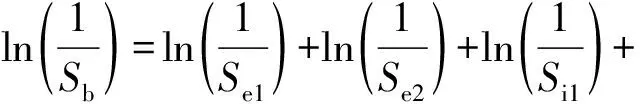
4个滚道中任一滚道出现疲劳破坏，那么整套轴承失效。故有:Le1=Le2=Li1=Li2=Lsb，代入上式，则整套轴承的基本额定寿命L10b为:

(16)

当外载荷已知时，(16)式实际上是关于L10b的一元非线性方程，运用Newton迭代法等数值解法可求出唯一解。(16)式也是绘制转盘轴承动载荷承载曲线的基本方程式。在绘制动载荷曲线时，L10b为定值(通常取30 000 r)，对于给定的轴向力Fa，(16)式是关于倾覆力矩M的一元方程，求解后可获得唯一解。求解出若干组(Fa,M)值后，依次连接即绘制出动载荷承载曲线。图3即为121.36.4000转盘轴承的动载荷承载能力曲线。

图3 动载荷承载能力曲线(寿命为30 000 r)

5 结束语

采用上述球-圆柱滚子组合转盘轴承承载能力的理论计算方法，开发出了相应的计算机软件。运用此软件对十余个型号的轴承进行了计算，并与国外某著名转盘轴承公司的计算结果进行了对比，结果表明，无论是承载曲线的形状还是计算结果两者都十分接近。文中叙述的理论方法为提高此类轴承设计质量，避免设计的盲目性奠定了基础。