基于ADAMS的推土机差速转向系统运动学分析

杨洪征,沈玉凤,张春明

(1.山东理工大学交通与车辆工程学院,山东淄博255049;2.山东理工大学机械工程学院,山东淄博255049)

液压机械双功率差速转向机构是目前履带式车辆较为先进的转向机构[1],它利用了机械传动高效率和液压传动无级变速的特点[2],组成了较为理想的传动装置.借助虚拟样机技术在计算机上建立差速转向机构的三维可视化模型,可以模拟现实环境下系统的运动学和动力学特性,克服传统计算无法精确反映机构实际运动和受力情况的缺点.本文利用Pro/E和ADAMS软件建立差速转向机构的虚拟样机,并在此基础上模拟实际工况和各种运动状态以进行仿真研究.

1 差速转向机构工作原理

如图1所示,差速转向机构主要由左右两个特性参数相同的行星排组成,动力由变速器锥齿轮轴和液压马达输入.右侧行星排的太阳轮通过连接齿轮与次级齿轮啮合,而左侧行星排的太阳轮通过连接齿轮和中间齿轮与次级齿轮啮合.当转向马达转动时,两侧行星排的太阳轮转速相等而转向相反,与相等的行星架转速线性合成后,使一侧的齿圈转速加快,另一侧的齿圈转速减慢,从而实现差速转向.

图1 差速转向机构简图

2 推土机差速转向机构建模

MSC/ADAMS是最著名的虚拟样机分析软件,它使用交互式图形环境和零件库、约束库、力库来创建完全参数化的机械系统动力学模型,可以对虚拟机械系统进行运动学、静力学和动力学分析.只要能保证机构的模型尺寸和约束定义精确,就能得到差速转向机构不同状态和负载下各部件的载荷、转速、扭矩等参数.

2.1 差速转向机构模型参数

差速转向机构模型参数是以SD23推土机为基础,由机械设计手册根据输入输出转矩和转速计算得到,差速转向机构各齿轮的基本参数见表1.

表1 差速转向机构基本参数

表1中:m为齿轮模数;z为齿数;x*为变位系数;b为齿宽.各齿轮的压力角均为20o.

2.2 虚拟样机几何模型的建立

图2 差速转向机构虚拟样机图

2.3 虚拟样机的约束条件

为建立的模型添加正确的约束是保证模型正常运转的重要条件,虚拟样机的约束条件主要包括:实现轴承功能的旋转副约束;地面和箱体之间的固定约束;齿轮与齿轮之间的接触约束;齿圈所受的转向阻力矩;液压动力和小锥齿轮的输入参数等.下面对主要约束分别进行说明.

2.3.1 接触约束

在接触力计算方法的选取上比较常用的是基于碰撞函数(IMPACT)的接触算法,ADAMS/Solver运用ADAMS函数库中IMPACT函数来计算接触力,建立的虚拟样机也采用了这种方法.

建立接触约束时,主要参数包括:Stiffness:指定材料刚度;Force Exponent:用来计算瞬时法向力中材料刚度项贡献值的指数;Damping:定义接触材料的阻尼属性;Penetration Depth:定义全阻尼(full damping)时的穿透值;Coulomb Friction:指定摩擦模型为dynamic friction;Static Coefficient(MU_STATIC):是当接触点滑动速度小于Stiction Transition Velocity值时的摩擦系数;Dynamic Coefficient(MU_DAN):是当接触点滑动速度大于Friction Transition Velocity值时的摩擦系数;Friction Transition Velocity:当滑动速度大于等于Friction Transition Velocity指定值时,摩擦系数为M U_DANAMIC;Stiction T ransition Velocity:当接触点滑动速度逐渐减小时,摩擦系数从MU_DANAMIC到MU_STATIC逐渐变化.参数选取如图3所示.

图3 接触参数的选择界面

2.3.2 转向阻力矩的确定

转向阻力矩与推土机的使用质量、履带宽度、接地长度、转向半径和土壤性质等有关.为简化计算,一般按空负荷工况计算转向阻力矩.可采用下式来计算履带推土机的齿圈所受转向阻力矩,即

式中:G为推土机使用重量;B为履带中心距;r为驱动轮半径为履带传动系数为履带长度;μ为转向阻力系数.当车辆以半径R转向时,μ可通过以下公式计算:

（114）四齿异萼苔 Heteroscyphus argutus（Reinw.Blume ＆ Nees）Schiffn. 熊源新等（2006）；杨志平（2006）；马俊改（2006）；李粉霞等（2011）；余夏君等（2018）

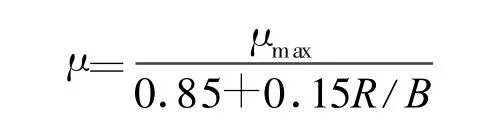
式中μmax=0.9.

2.3.3 滚动阻力矩的确定

假设推土机在坚实土壤上运动,滚动阻力系数f各档位均取0.1,则齿圈所受滚动阻力矩为

2.3.4 运动学关系式

由行星排的特性方程[4]可知:

由

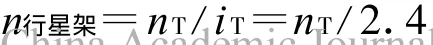
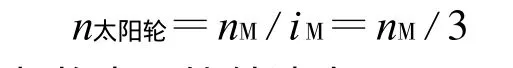
得差速转向机构齿圈的转速为

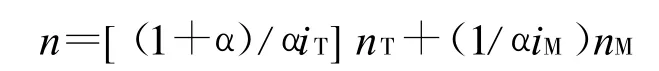
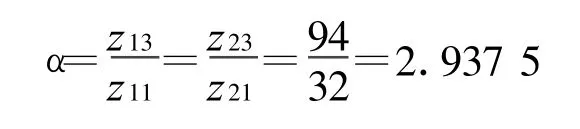
由于转向马达工作时,左右行星排太阳轮转速大小相等,方向相反,则推土机差速转向机构左右齿圈转速为

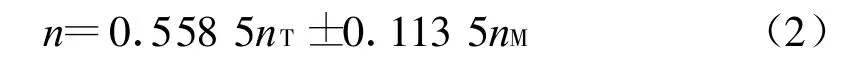
2.3.5 输入转速的确定

SD23履带推土机速度参数见表2,假设推土机以二档正常行驶,则推土机变速器输出轴转速为

表2 推土机速度参数表

3 虚拟样机分析结果

安装机械液压双功率流差速转向机构后,推土机可以按照任意转向半径转向,能满足小场地及特殊场合的施工要求.下面通过几种典型的运动状态进行分析.

3.1 直线行驶状态分析

直线行驶状态中,差速转向机构齿圈所受转矩为2 628.2 N◦m,输入转速nT=403.2(°)/s,齿圈理论转速n=225.19(°)/s,齿圈转速随时间的变化曲线如图4所示.只有变速器锥齿轮输入动力时,差速转向机构左右齿圈转速差(如图4中曲线3所示)的平均值为0.004 9,说明该机构直线行驶时,两侧齿圈转速相同,偏驶率几乎为0.

3.2 原地转向工况分析

推土机原地转向时,即推土机转向半径R等于推土机履带中心距的一半,由公式(1)得左右两侧齿圈所受阻力矩为

38 381.7 N◦m

转向液压马达单独工作时,输入转速设定为:nM=1 060(°)/s,由公式(2)得齿圈理论转速为:n=±0.113 5×nM=±120.31(°)/s.齿圈输出转速曲线如图5所示.

从图5中可以看出,液压马达单独工作时左右齿圈转速相对稳定,两侧齿圈转向相反,曲线3为两侧齿圈瞬时转速差,可以看出推土机瞬时转动中心不固定.转速差的均值占平均转速的百分比为

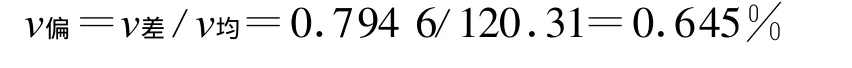
因此本差速式转向机构在只有液压马达输入时,可以实现一侧履带正转,另一侧履带反转,转向半径很小且近于零.

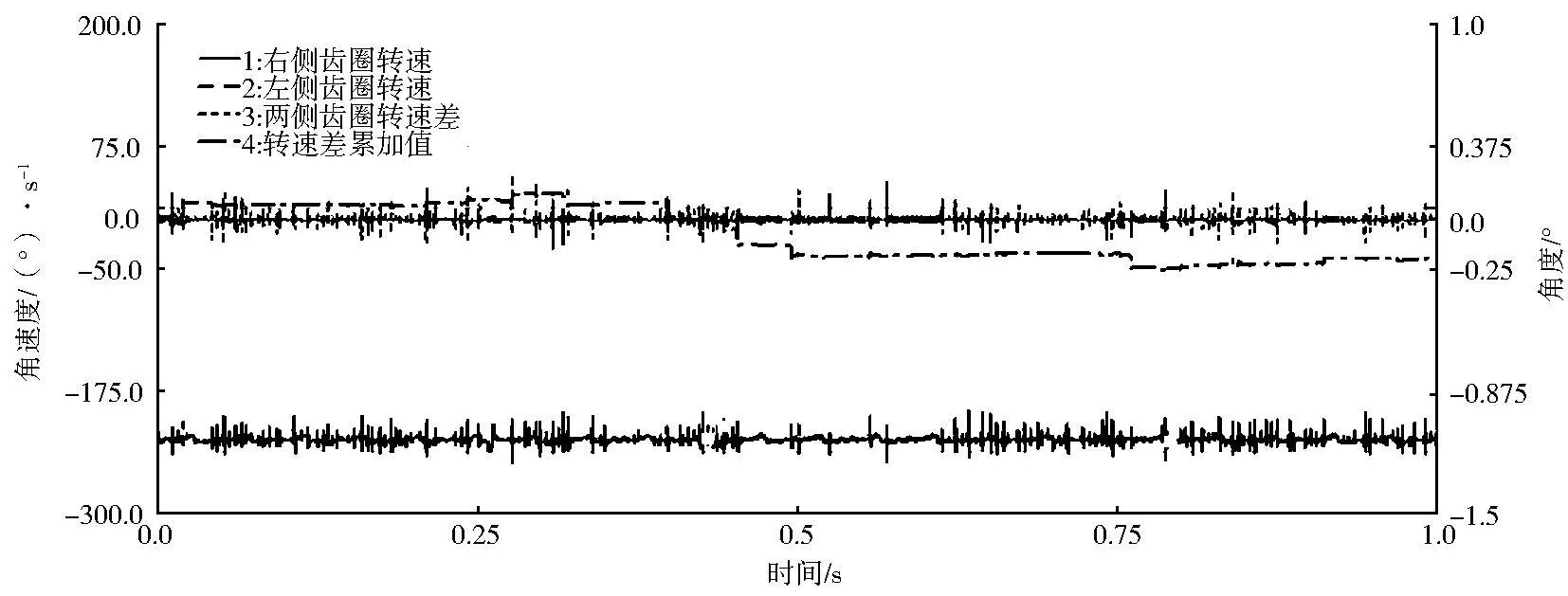
图4 直线行驶时差速转向机构输出曲线

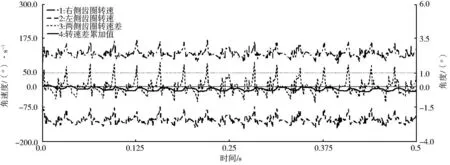
图5 原地转向工况下差速转向机构输出曲线

图6 一般运动状态差速转向机构输出曲线

3.3 一般运动状态分析

当变速器锥齿轮和液压马达共同提供动力时,左右齿圈转速曲线如图6所示,此时液压马达输入转速nM=360(°)/s,锥齿轮输入转速nT=403.2(°)/s.从图6中可以看出,当两个动力源共同输入动力时,该差速转向机构运行平稳,可以实现一侧转速高,另一侧转速低,从而实现差速转向.

4 结束语

推土机差速转向机构从设计到成熟要经历一个长期实践检验的过程,使用ADAMS软件建立机构的虚拟样机模型,对虚拟样机进行模拟实际工况的仿真研究,可以及时地反映设计中的不合理因素,而分析得到的受力数据可以直接导入到ANSYS等有限元分析软件,为系统各零部件的结构和优化分析提供数据,从而减少设计费用和设计周期.因此,使用虚拟样机技术对差速转向机构进行分析、设计、改进是一种可行的分析方法.

[1] 张娉娉,邹广德,张为春.履带式推土机差速转向机构的设计与计算[J] .建筑机械,2008(3):79-82.

[2] 迟媛,蒋恩臣.履带车辆差速式转向机构性能试验[J] .农业机械学报,2008,39(7):14-17.

[3] 张小明,冷军发,刘波.基于ADAMS的单缸内燃机动力学分析与研究[J] .机械传动,2009,33(4).52-54.

[4] 赵建军.履带车辆差速式转向机构动力学分析与比较[J] .工程机械,2002,33(8):18-21.