双曲线ISO代码译成差分插补代码及程序的实现

刘 肖,赵庆志,于光伟,张 健

(山东理工大学机械工程学院,山东淄博255049)

在数控机床控制系统的设计中,输入的包含工件信息的ISO代码是根据不同的插补原理,通过编程翻译成的相应代码.对数控系统来说,插补是最重要的计算任务.目前普遍采用的插补算法有两大类:一类是脉冲增量插补,如逐点比较法[1]、数字积分法、比较积分法[2]、矢量判断法等;另一类是数据采样插补[3].本文采用的差分插补原理[4]基于多项式函数插值拟合的理论,具有很多的优点,可计算曲线的某点函数值、一阶、二阶导数、曲率半径、判断曲线的凸凹性,适合于任意圆锥曲线(包括直线,圆弧,椭圆,抛物线,双曲线等)的插补,尤其是非圆曲线的插补.用差分插补原理可编制通用化模块程序[5],本文着重论述双曲线ISO代码译成差分插补代码的方法.

1 基于差分插补原理的曲线方程坐标系变换及5B代码定义

设X轴始终水平向右、Y轴始终垂直向上、坐标原点不定的坐标系为绝对坐标系,象限定义为L41、L42、L43、L44.以加工曲线起点为坐标原点,起点的切线方向在第一象限建立的坐标系为相对坐标系.将绝对坐标系中的曲线表达式转化为相对坐标系中正二次曲线表达式[2]得到

则差分插补代码定义为

其中

j x1,jy1,j x2,jy2分别叫X的一阶差分,Y的一阶差分,X的二阶差分,Y的二阶差分;j j是计数长度,在相对坐标系下,设曲线终点的导数绝对值为K,当K＞1时,计数方向Gxy=79,此时j j为曲线在Y轴按计数方向的投影长度.当K≤1时,计数方向Gxy=78,jj为曲线在X轴按计数方向的投影长度;lxy表示在以曲线起点为原点的绝对坐标系中,曲线起点的切线方向所在的象限号.在曲线插补过程中,要始终保证j x1＞0且j y1＞0,以使曲线加工沿着曲线的走向.

2 顺时针双曲线ISO代码转化

顺时针双曲线ISO代码的定义为

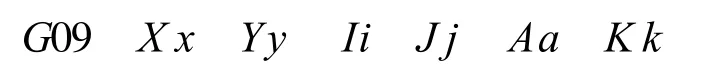
其中:(x,y)为双曲线终点相对起点的坐标;(i,j)为双曲线的顶点相对起点的坐标;a为实半轴长度;k=0表示双曲线以X轴为实轴,k=1表示双曲线以Y轴为实轴,双曲线的标准方程为

则(-i,-j)满足式(3),即

2.1 顺时针双曲线相对坐标编程

1)k=0&&y<0,即以X轴为实轴,左边的那条双曲线,如图1所示.

(1)当i＞0&&j<0时,曲线起点在第二象限,此时双曲线在相对坐标下的方程为

整理为式(1)形式的表达式得

则差分插补代码为

对式(4)求导数确定计数方向和计数长度:(i)当|j2(x-i-a)|＞i|(j+y)(i+2a)时,Gxy=79,j j=|y|;

(ii)当|j2(x-i-a)|≤i|(j+y)(i+2a)|时,Gxy=78;当|y|≤|j|时,j j=x;当|y|＞|j|时,jj=2i-x.

(2)当i=0&&y<0时,曲线起点在X轴上,此时双曲线在相对坐标下的方程为

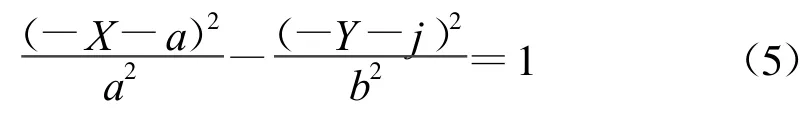
整理为式(1)形式的表达式得

图1 k=0&&y<0时双曲线

则差分插补代码为

对式(5)求导数确定计数方向和计数长度:

(i)当|y(x+a)|＞|x(x-2a)|时,Gxy=79,jj=|y|;

(ii)当|y(x+a)|≤|x(x-2a)时,Gxy=78,j j=|x|.

(3)当i＞0&&j＞0时,曲线起点在第三象限,此时双曲线在相对坐标下曲线方程为

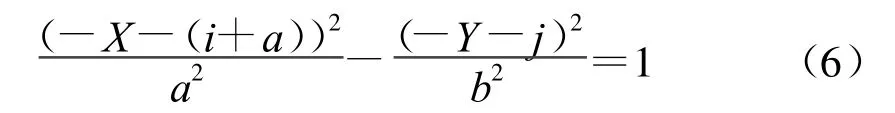
整理为式(1)形式的表达式得

则差分插补代码为

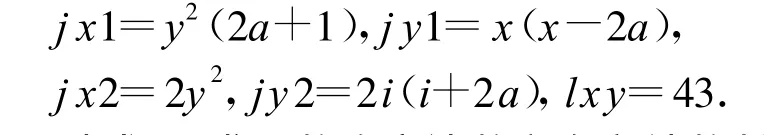
对式(6)求导数确定计数方向和计数长度:

(i)当|j2(x+i+a)|＞i|(j+y)(i+2a)时,Gxy=79,jj=|y|;

(ii)当|j2(x+i+a)≤i|(j+y)(i+2a)|时,Gxy=78,jj=|x|.

2)k=0&&y＞0,即以X轴为实轴,右边的那条双曲线,如图2所示.

(1)当i<0&&j＞0时,曲线起点在第四象限,此时双曲线在相对坐标下曲线方程为

整理为式(1)形式的表达式得

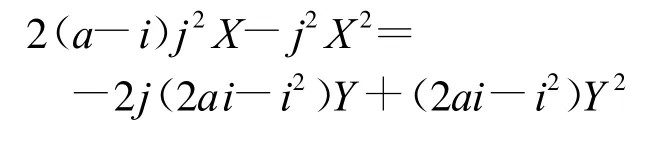
则差分插补代码为

图2 k=0&&y＞0时双曲线

对式(7)求导数确定计数方向和计数长度:

(i)当|j2(x-i-a)|＞i|(j-y)(i-2a)时,Gxy=79,j j=y;

(ii)当|j2(x-i-a)|≤i|(j-y)(i-2a)|时,Gxy=78;当y≤j时,jj=x;当y＞j时,j j=2|i|+x.

(2)当i=0&&y＞0时,曲线起点在X轴上,此时双曲线在相对坐标下曲线方程为

整理为式(1)形式的表达式得

则差分插补代码为

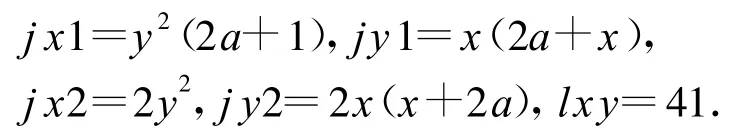
对式(8)求导数确定计数方向和计数长度:

(i)当|y(x+a)|＞|x(x+2a)|时,Gxy=79,j j=y;

(ii)当|y(x+a)|≤|x(x+2a)|时,Gxy=78,j j=x.

(3)当i<0&&j<0时,曲线起点在第一象限,此时双曲线在相对坐标下曲线方程为

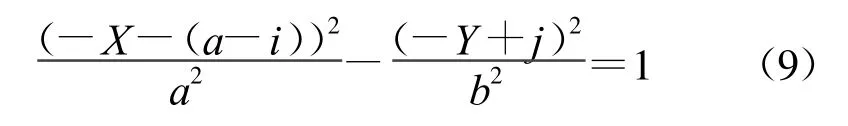
整理为式(1)形式的表达式得

则差分插补代码为

对式(9)求导数确定计数方向和计数长度:

(i)当|j2(x+a-j)|＞i|(y-j)(i-2a)|时,Gxy=79,j j=|y|;

(ii)当|j2(x+a-j)|≤i|(y-j)(i-2a)|时,Gxy=78,jj=|x|.

3)k=1&&x<0,即以Y轴为实轴,上边的那条双曲线,如图3所示.

图3 k=1&&x<0时双曲线

(1)当i<0&&j<0时,曲线起点在第一象限,此时双曲线在相对坐标下曲线方程为

整理为式(1)形式的表达式得

则差分插补代码为

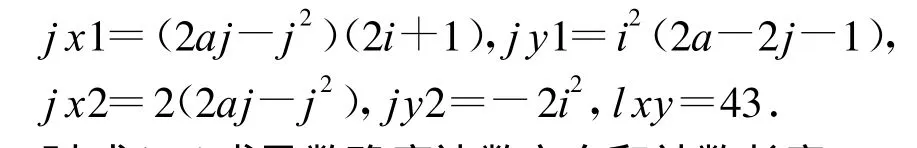
对式(10)求导数确定计数方向和计数长度:

(i)当|(2aj-j2)(x+i)|＞i2|(a-j-y)|时,Gxy=79,当|x|≤|i|时,j j=|y|;当|x|＞|i|时,jj=2|j|+y;

(ii)当|(2aj-j2)(x+i)|≤i2|(a-j-y)|时,Gxy=78,jj=|y|.

(2)当x<0&&j=0时,曲线起点在Y轴上,此时双曲线在相对坐标下曲线方程为

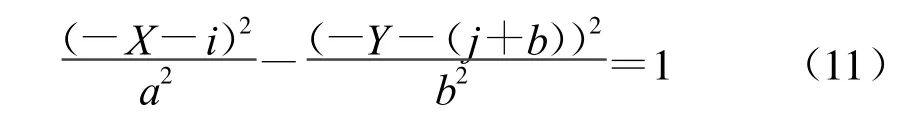
整理为式(1)形式的表达式得

则差分插补代码为

对式(11)求导数确定计数方向和计数长度:

(i)当|(2a+y)y|＞|x(a+y)|时,Gxy=79,jj=|y|;

(ii)当|(2a+y)y|≤x(a+y)|时,Gxy=78,jj=|x|.

(3)当i＞0&&j<0时,曲线起点在第二象限,此时双曲线在相对坐标下曲线方程为

整理为式(1)形式的表达式得

则差分插补代码为

对式(12)求导数确定计数方向和计数长度:

(i)当|(2aj-j2)(x+i)|＞i2|(a-j+y)|时,Gxy=79,j j=|y|;

(ii)当|(2aj-j2)(x+i)|≤i2|(a-j+y)|时,Gxy=78,j j=|x|.

4)k=1&&x＞0,即以Y轴为实轴,下边的那条双曲线,如图4所示.

图4 k=1&&x＞0时双曲线

(1)当i＞0&&j＞0时,曲线起点在第三象限,此时双曲线在相对坐标下曲线方程为

整理为式(1)形式的表达式得

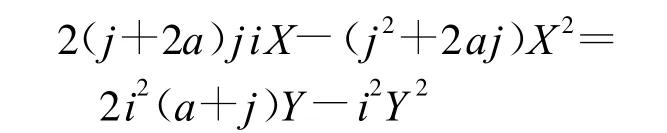
则差分插补代码为

对式(13)求导数确定计数方向和计数长度:

(i)当|(2aj+j2)(x-i)|＞i2|(a+j-y)|时,Gxy=79,当|x|≤|i|时,j j=|y|;当|x|＞|i|时,jj=2|j|-y;

(ii)当|(2aj+j2)(x-i)|≤i2|(a+j-y)|时,Gxy=78,jj=|x|.

(2)当x＞0&&j=0时,曲线起点在Y轴上,此时双曲线在相对坐标下曲线方程为

整理为式(1)形式的表达式得

则差分插补代码为:

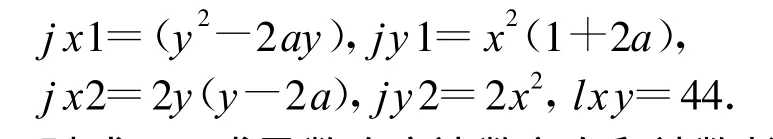
对式(14)求导数确定计数方向和计数长度:

(i)当|y(y-2a)|＞|(y+a)x|时,Gxy=79,jj=|y|;

(ii)当|y(y-2a)|≤|(y+a)x|时,Gxy=78,jj=|x|.

(3)当i<0&&j＞0时,曲线起点在第四象限,此时双曲线在相对坐标下曲线方程为

整理为式(1)形式的表达式得

则差分插补代码为

对式(15)求导数确定计数方向和计数长度:

(i)当|(j2+2aj)(x-i)|＞i2|(y+a+j)|时,Gxy=79,j j=|y|;

(ii)当|(j2+2aj)(x-i)|≤i2|(y+a+j)|时,Gxy=78,j j=|x|.

2.2 顺时针双曲线绝对坐标编程

在顺时针双曲线ISO代码前加上一条语句:G90X0Y0,用i=i-x0,j=j-y0,x=x-x0,y=yy0计算后代入相对坐标程序,即可转化为5B代码

逆时针双曲线ISO代码的定义为

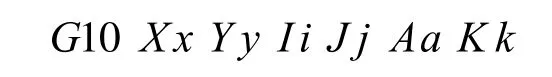
其转化的方法与顺时针双曲线ISO代码转化一样,不再赘述.

3 译码程序实现

译码过程一般通过数组或链表加上文件类的操作来完成,分为词法、语法检查和数值处理过程,通过刀补处理,将结果放入译码结果缓冲区中,再进行插补、位控等后续操作.本实例在Window XP系统下用C++Builder6.0进行了程序编制,定义了数组链表,结构如下:

把存储双曲线信息的文件shuangquxian.dat翻译成相应的5b.dat,结果正确.

4 实例

N010G10X0 Y-60 I-8J-30A20

K0//逆时针双曲线加工代码

图5 差分插补代码

形成的差分插补代码如图5所示.演示结果如图6所示,表明验证结果正确.

图6 演示结果

5 结束语

对于非圆曲线的加工,一般数控系统都是采用直线和圆弧来进行拟合,本文采用的差分插补算法可以直接加工非圆曲线,例如一些特殊曲线由椭圆,双曲线,抛物线等组合成的零件曲线,这样就避免产生拟合误差,在提高加工精度的基础上也提高了加工效率,在实际生产中已经得到了验证.

[1] 刘万菊,赵长明.逐步比较法渐开线插补的研究[J] .汽车工艺与材料,1999(2):17-19.

[2] 王琨琦,王润孝,孙林丽.椭圆曲线的比较积分插补方法研究[J] .西安工业学院学报,2005,25(1):1-2,7.

[3] 赵玉刚.宋现春.数控技术[M] .北京:机械工业出版社,2003.

[4] 王敏.差分插补方法及其在数控线切割机中的应用(一)[J] .电加工,1981(4):16-22.

[5] 赵庆志.基于可重构理论的慢走丝线切割机床控制系统研究与设计[D] .南京:南京航空航天大学,2004.