纯工况和联合工况下MF-Tyre模型的参数辨识
韦尧兵,赵学美,姜祖啸
(1.兰州理工大学机电工程学院,甘肃兰州730050;2.上海大众汽车有限公司,上海201805)
MF-Tyre模型是广泛应用于车辆动力学仿真和控制的半经验轮胎模型,能在稳态和瞬态工况下快速、准确地模拟出轮胎和路面间的接触力和力矩,可以全面表达轮胎在各种工况下的六分力特性和处理复杂的轮胎运动输入,包括大侧偏角(可超过30°)、大滑移率(100%)、大侧倾角(新版本可以处理摩托车模型的侧倾特性)和大负载(重型卡车),MFTyre模型还具有良好的包容特性,可对车辆模型进行平顺性仿真且结果较为准确[1].
目前,国内外对MF-Tyre模型参数辨识进行了广泛的研究,为了从试验数据中辨识出Magic Formula模型参数,早期TNO研究所通过Fortran的NAG子程序中的E04FDF编写了一套辨识软件对其进行参数辨识[2],该辨识算法对参数初值的选定比较敏感,如果初值选择不合理,辨识效果极差;基于遗传算法的IMMa优化算法虽然具有较强的鲁棒性[3],但此方法收敛速度慢,耗时长;基于遗传算法和数值算法的混合优化算法进行参数辨识[4]的方法在具体实现时过于复杂,在辨识联合工况时尤为突出.本文将利用Matlab优化工具箱的L-M Method优化算法对最新的MF-Tyre 6.1.1模型进行纯工况和联合工况(5个工况)的轮胎参数辨识,并对辨识结果进行残差分析.
1 MF-Tyre模型建模原理
MF-Tyre模型是基于轮胎物理原型的一套数学表达式,其输入输出关系如图1所示.图1中,输入为纵向滑移率κ、侧偏角α、侧倾角γ和垂直载荷Fz,输出为轮胎的纵向力Fx、侧向力Fy、翻转力矩Mz、滚动阻力矩My和回正力矩Mz.

图1 M F-T yre模型的输入输出关系
MF-Tyre模型的一种形式为sin形式[5],用来确定纵向力Fx和侧向力Fy,即

式中:Y为模型的输出,即轮胎纵向力Fx或侧向力;X为模型的输入,即侧偏角α或纵向滑移率κ;为水平偏移为垂直偏移;D、C、B、E为曲线有关的参数.
MF-Tyre模型的另一种形式为cos形式[5],用来确定回正力矩Mz,即

本文参数辨识对象是2009年1月发布的最新版MF-Tyre 6.1.1模型,它结合了以前版本的优点,并在以下几个方面进行了改进[1]:引入胎压对轮胎刚度、滚动阻力及其他特性因素的影响;改进了摩托车轮胎模型的路面接触模型;采用鲁棒性更好和更为精确的椭圆接触法替换二维路面接触法,椭圆函数在二维和三维路面接触中都适用,具有向后兼容性;调整了纵向速度函数中侧倾翻转力矩影响因子;新版本能直接支持ADAMS2008r1.
2 L-M Method辨识理论与MF-Tyre
2.1 L-M Method辨识原理
用于解决非线性最小二乘问题的L-M Method是基于Gauss-Newton的一种改进优化算法,其建模原理在很多文献中有所描述[6].用此方法对MFTyre模型参数进行辨识时,首先要构造目标函数E(X),该函数为模型计算值与试验数值差的平方和,即

式中,Fpacejke为MF-Tyre模型计算出的轮胎力或力矩;FTest为试验测试出的轮胎力或力矩;X为待辨识参数;n为试验测试采样点数;p为试验测试变换的载荷次数;q为试验测试变换的外倾角次数.
其迭代关系如下:

式中:e(X)为误差;J(X)是E(X)的Jacobian矩阵;比例系数μ>0为常数;I为单位矩阵.由于各个工况模型参数的物理意义比较明确,加快了算法的收敛速度,而且MF-Tyre模型参数辨识的精度也较高.
2.2 L-M算法辨识流程
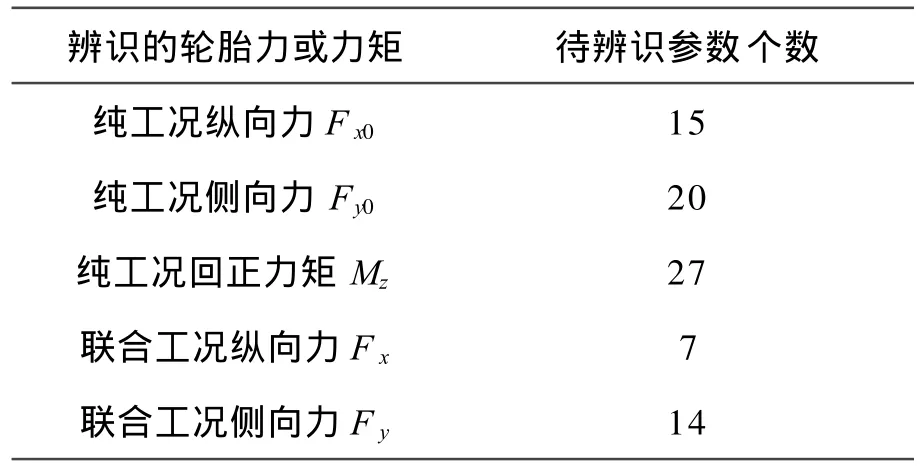
①设定误差允许值ε=1~10(此值较大,主要因为试验数据本身很大,且迭代次数较多,如果允许误差值过小,会引起求解失败,无法得到所需要的模型参数),μ=0.1,β=5,其它需要求解的模型参数Xi全部设为1.
②计算FPacejka(Xk,)值,并得到误差目标函数.
③计算误差目标函数的Jacobian矩阵J(X).
④计算Δ X.
⑤若E(Xk)<ε,转到⑦;否则计算XK+1,并计算误差目标函数E(Xk+1).
⑥若E(Xk+1) ⑦停止. MF-Tyre模型参数,是从试验数据中辨识出来的,辨识的过程也可看作一个拟合过程.应用全局辨识方法对MF-Tyre 6.1.1模型进行参数辨识,辨识流程如图2所示.首先利用纯纵滑试验数据辨识出轮胎纯纵向力参数;然后利用纯侧偏试验数据辨识出轮胎纯侧向力和回正力矩参数;接着利用已辨识出的纯纵向力参数和联合工况试验数据辨识出联合工况轮胎纵向力拟合参数;最后利用已辨识出的纯侧向力参数和联合工况试验数据辨识出联合工况轮胎侧向力复合参数. 图2 M F-T yre模型参数辨识流程 本文采用轮胎为某公司生产的215/55R16型号轮胎,其试验条件如下:纯纵滑纵向力试验数据:纵向滑移率κ的参数值分别为0.1,0.2,0.3,0.4,0.6,0.8,1.0,外倾角γ为2°,垂直载荷Fx分别为2 kN,4 kN,6 kN;纯侧偏侧向力试验数据:侧偏角α分别为外倾角γ为垂直载荷Fx分别为2 kN,4 kN,6 kN;联合工况试验数据:纵向滑移率κ分别为0.1,0.2,0.3,0.4,0.6,0.8,1,侧偏角α分别为外倾角γ为垂直载荷Fx分别为2 kN,4 kN,6 kN. 最新的MF-Tyre6.1.1模型对应的待辨识参数见表1,5个工况需要辨识出83个参数. 表1 MF-Tyre6.1.1模型的待辨识参数 1)纯纵滑工况轮胎纵向力Fx0模型参数辨识 纯纵滑工况的轮胎纵向力Fx0是滑移率κ、外倾角γ和垂直载荷Fz的函数.纵向力Fx0模型参数辨识的优化目标函数为 2)纯侧偏工况轮胎侧向力Fy0模型参数辨识 纯侧偏工况轮胎侧向力Fy0是侧偏角α、外倾角γ和垂直载荷Fz的函数.侧向力Fy0模型参数辨识的优化目标函数为 3)纯侧偏工况的回正力矩Mz模型参数辨识纯侧偏工况的轮胎回正力矩Mz是侧偏角α、外倾角γ和垂直载荷Fz的函数.对Mz参数进行辨识要用到2)中辨识出的侧向力参数.回正力矩Mz模型参数辨识的优化目标函数为 4)联合工况轮胎纵向力Fx模型参数辨识 联合工况中的轮胎侧向力Fx是侧偏角α,滑移率κ和垂直载荷Fz的函数.利用已辨识的纯纵向力参数和联合工况试验数据来辨识联合工况轮胎侧向力复合参数.联合工况轮胎侧向力Fx模型参数辨识的优化目标函数为 5)联合工况轮胎侧向力Fy模型参数辨识 联合工况中轮胎纵向力Fy是侧偏角α,滑移率κ,垂直载荷Fz的函数.利用已辨识的纯侧向力参数和联合工况试验数据来辨识出联合工况轮胎侧向力拟合参数.联合工况轮胎纵向力Fy模型参数辨识的优化目标函数为 式(8)、式(10)、式(12)、式(14)、式(16)中,待辨识模型参数的物理意义在相关文献中有所描述[7],在此不再做具体说明. 将试验测得的轮胎力/力矩和MF-Tyre模型计算的轮胎力/力矩绘制成曲线,如图3~图7所示. 由图3~图7可以看出,通过参数识别所获得的MF-Tyre模型力/力矩特性曲线与实验数据十分吻合,表明L-M Method优化算法具有很高的辨识精度. 图3 纯工况纵向力辨识结果 图4 纯工况侧向力辨识结果 图5 纯工况回正力矩辨识结果 图6 联合工况纵向力辨识结果 图7 联合工况侧向力辨识结果 利用拟合曲线与试验曲线的对比图,可以在整体上比较直观地比较模型的拟合效果.但是,当拟合误差很小时,只观察曲线对比图,难以对模型的拟合精度做精确的评价.为此,引入参数识别的残差MSE分析作为模型精度评价的一个指标,且 MF-Tyre模型参数辨识结果的残差MSE见表2,其中残差保持在5%以下,进一步说明采用L-M Method优化算法能够得到较高的拟合精度. 表2 辨识出的模型参数拟合精度% 1)对MF-Tyre6.1.1模型的辨识流程和辨识算法进行了研究和分析,结合一整套完整的215/55R16轮胎数据辨识出了包括联合工况在内的5个工况的83个参数. 2)对辨识结果进行了残差MSE分析,结果表明残差保持在5%以下,说明采用L-M Method优化算法能够得到较高的拟合精度. [1] TNO Automotive.MF-tyre&MF-swift 6.1 user Manual[R] .USA:T NO Automotive,2008. [2] Cabrera J A,Ortiz A,Carabias E.An alternative method to de-2.3 轮胎参数辨识流程

3 辨识结果分析
3.1 轮胎试验及5工况辨识结果
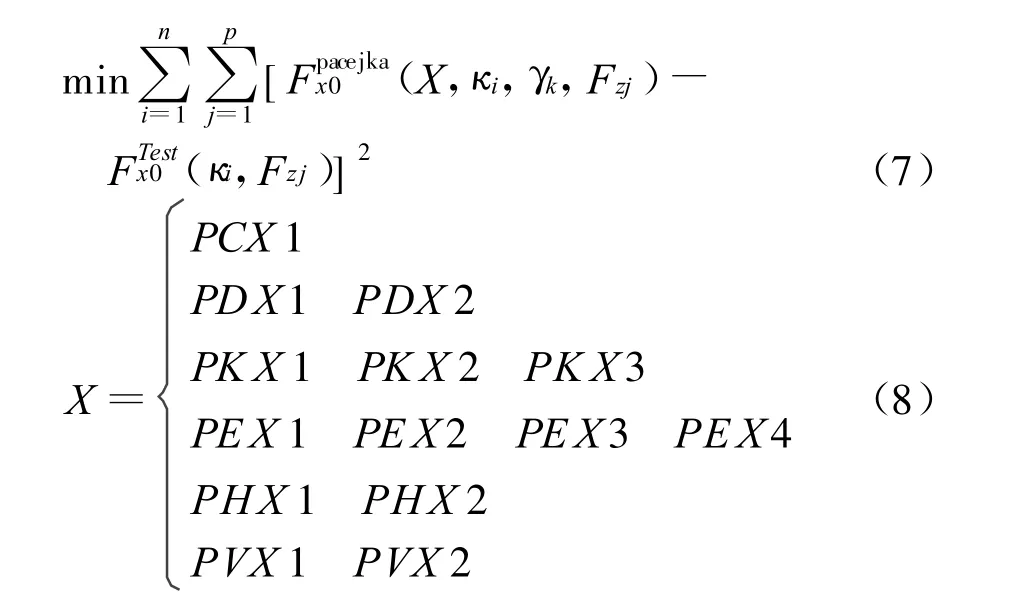

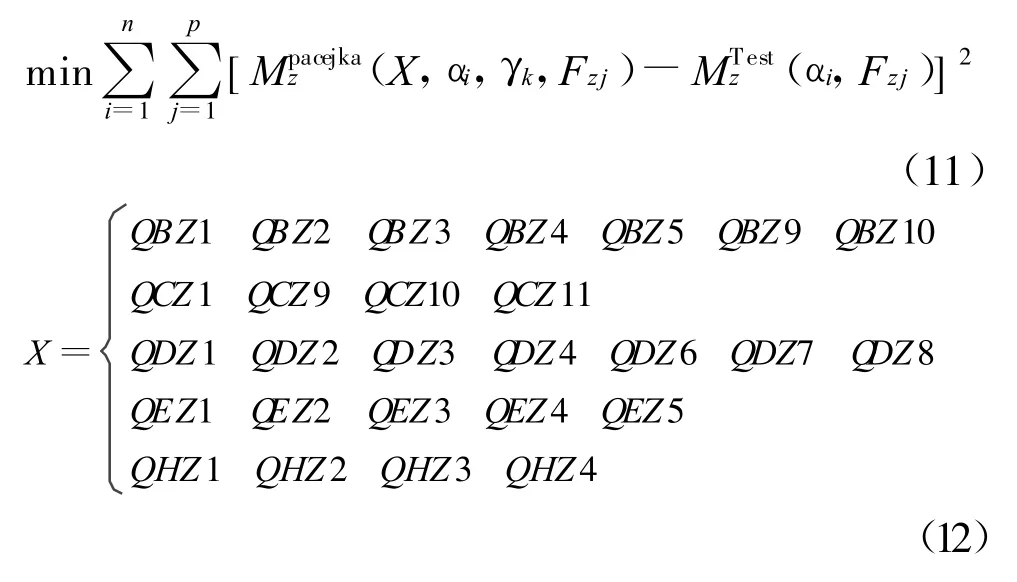

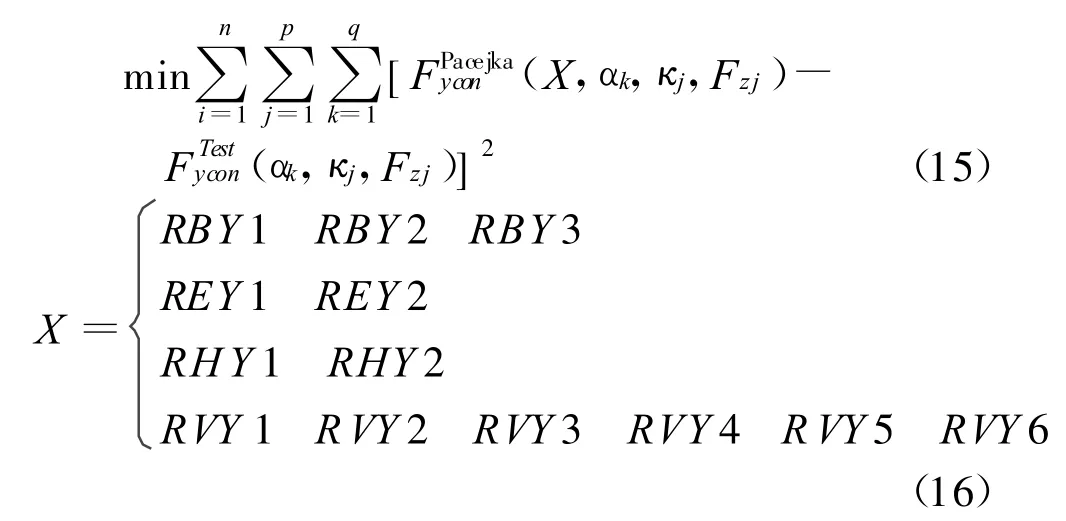




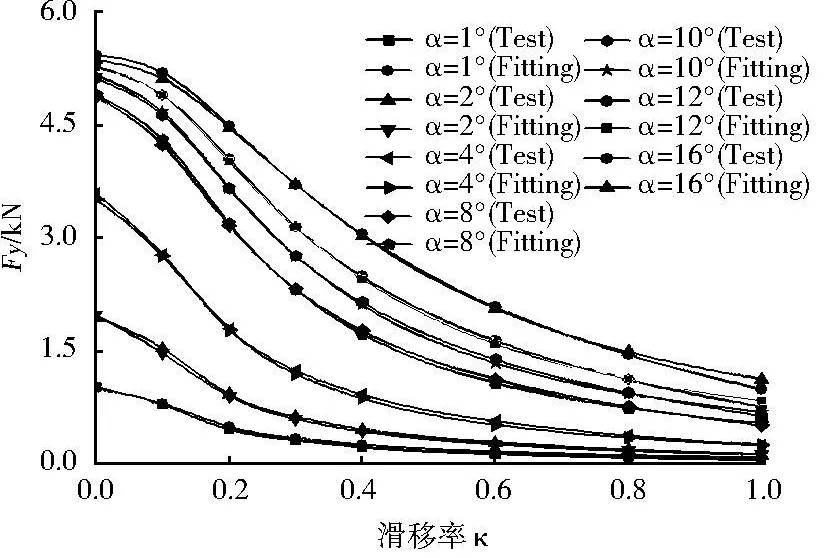
3.2 精度评价


4 结论

