尾部条件期望约束下最优保险合同的选择

高志强，张梦琳

（南开大学 风险管理与保险学系，天津 300071）

0 引言

尾部条件期望（Tail probability expectation,CTE）是一个优于在险价值（Value at Risk，VaR）的风险度量指标，也是目前最常用的风险度量指标。

因此，以CTE代替VaR作为约束条件，是具有积极意义的。本文的目的就是完成这一任务，并从中得到一些有用的结论。本文的贡献和创新主要有以下两个方面：第一，本文将CTE引入了最优保险合同的研究领域。尽管CTE的性质优于VaR，但是其计算也更加复杂。在优化的过程中，本文采用了大量的分情况讨论，用以代替复杂的数学计算。第二，本文将免赔额保险同赔款上限保险结合在一起考虑，过程更加一般化。之前的研究不允许保险合同中同时具有免赔额和赔款上限，将其视为两种保险合同。本文称这种同时具有免赔额和赔款上限的保险合同为一般保险合同，实际上免赔额保险是一般保险的一种特殊形式。

本文假设保费为比例保费，是损失期望的一定比例。在这一假设条件下，本文发现免赔额保险总是最优的保险方式。本文对CTE限定下最优保险合同的研究只是初探，该方面的研究还远未完成，有很多可以继续进行的地方，譬如采用其他形式的保费、引入效应函数等等。希望有更多的学者投入到该领域的研究中。

1 模型的构建

1.1 风险度量指标

最优保险合同的计算是在一定的约束条件下进行的，而约束条件的目的是将投保人的风险控制在一定程度内，因此，首先要确定一个合适的风险度量指标。尽管VaR也是一个被广泛使用的风险度量指标，但是相关研究证明CTE更加优秀。一致性是对风险度量指标非常重要的一个性质，Artzner（1999）、Pflug（2000）证明 CTE 具有一致性的性质，而VaR则不具有该性质。Bucay、Rosen（1999）较早的将CTE用于信用风险的度量中。随后，更多的学者将其用于优化问题，如 Uryasev（2000、2002），Jun Cai、Ken Seng Tan（2007）等。

如果是一个连续型随机变量，VaRα(X)是满足式的唯一解：

CTE通常通过F式来计算：

通常情况下，α的取值小于5%。但是当VaRα(X)值附件存在概率质量的话，也就是说如果存在ε>0，使得VaRα(X)=VaRα-β，式（1）和式（2）的计算方法就不再适用。 此时，应该调整为：

设 β=min{γ∶VaRγ(X)=VaRα(X)}，有：1.2 假设条件

假设投保人最初的财富值为W0，其面对的风险所造成的损失为X，X是一个 [0，T]内分布的非负的连续型随机变量，密度函数为f(x)，分布函数为F(x)。为了管理风险，投保人选择了购买保险。当损失为x时，保险合同补偿的金额为I(x)，0≤I(x)≤x。保费为P，是保险人补偿金额的期望值的一定比例，P=λE[I(X)]。购买保险后，投保人的财富变为W0-P；发生损失后，投保人的财富变为W0-P-X+I(X)。因此，购买保险后，投保人可能的损失为(W0-P)-[W0-P-X+I(X)]=X-I(X)。现在将R(X)=X-I(X)定义为投保人的自留风险。由于X是一个随机变量，因此R(X)也是一个随机变量。投保人希望将自留风险控制在可接受的范围内，即约束条件为CTEα[R(X)]≤N。其中，1-α是置信区间，N代表投保人可以承受的风险。1.3 最优保险合同问题

本文构建的最优保险合同的模型，是在保证一定的安全程度下，使得保费最小，具体表示为：在CTEα[R(X)]≤N的约束条件下，最小化P。如果要使得自留风险更小，也就是使CTEα[R(X)]更小，投保人需要购买更多的保险。因此，要使得保费最小，原约束条件等同于CTEα[R(X)]=N。再来看P，因为P=λE[I(X)]，而λ是一个固定的值，因此最小化的目标可以变为E[I（X）]。因此，本文需要解决的问题是在满足CTEα[R(X)]=N的约束条件下，选择一定的保险合同，使得E[I（X）]最小。

本文比较的是两种最重要的保险合同：一般保险合同和比例保险合同。首先，本文通过对不同的免赔额和赔款上限的讨论，选择一般保险合同中的最优形式；然后，本文将最优的一般保险合同与比例保险合同进行比较，最终选出一个最优保险合同。

2 一般保险合同

2.1 一般保险合同的形式

之前的研究都是将具有免赔额的保险与具有赔款上限的保险区分开，如 Wang（2005）、Hung-Hsi Huang（2006）等。实际上，投保人在保险合同中可以同时选择免赔额和赔款上限，这样投保的风险较少，需缴纳的保费也相应较少。当一般保险合同中免赔额为0时，一般保险合同就变为赔款上限保险；当一般保险合同中赔款上限为损失最大值时，一般保险合同就变为免赔额的保险。可见，一般保险合同是一种更一般的保险合同。

设一般保险合同中，免赔额为a，赔款上限为b，0≤a≤b≤T。发生损失后，保险公司对投保人的赔付为：

因此，投保人的自留风险为：

由式（6）可知，R（x）是一个关于 x的非递减函数，不难证明 VaRα[R(X)]=R[VaRα(X)]

2.2 对免赔额及赔款上限的讨论

直接研究CTE约束下最优一般保险合同的问题会非常复杂，这里首先探讨免赔额、赔款上限和VaRα(X)在不同位置关系下的最优一般保险合同，为后文的分析做准备工作，现在分三种情况对免赔额及赔款上限进行讨论：

2.2.1 b≤VaRα(X)

这种情况下，R(x)与x的关系如图1所示。曲线R(x)交x于D点，设D点纵坐标为d。此时，最优问题的约束条件为：

根据图 1，不难得出 VaRα(X)=d+(b-a)。 由式（7）可知，当N确定后，d也是确定的，由于VaRα(X)也是确定的，因此，免赔额和赔款上限的选择要满足b-a=VaRα(X)-d。此时，a是关于b的函数，并且满足da/db=1。现在的目标是使式（8）最小化。

将式（8）相对b进行求导，并代入da/db=1，得到：

图1 投保人的自留风险（实线部分）

很明显式小于0。因此，式（8）是关于b的减函数。当b=VaRα(X)时，式(8)取得最小值。

结论一：b≤VaRα(X)时，最优的保险合同形式是赔款上限等于 VaRα(X)。

2.2.2 a＜VaRα(X)＜b这种情况下，约束条件可以写为：

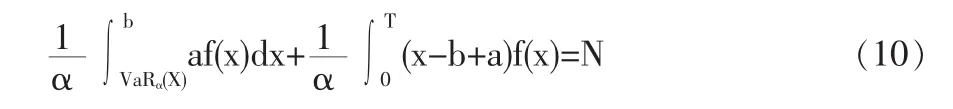
最小化的目标是：

由式（10）可知，此时a是关于b的函数。将式(10)两边关于b求导，可以得到da/db的值。将式（11）对b进行求导，并代入由式得到的da/db的值，有：

将式（12）继续对b进行求导，得到：

因为 a＜Varα(X)，所以当 b=T 时，式（12）等于0，式（13）大于 0。 因此，式（11）在 b=T 时取最小值。

结论二：a＜VaRα(X)＜b 时，最优的保险合同形式是免赔额保险。

2.2.3 VaRα(X)≤a

在这种情况下，约束条件可以写作：

最小化的目标是：

将式（14）代入式（15），不难发现式（15）是一个固定的值。也就是说，在满足约束条件的情况下，免赔额和最高限额的选择并不影响保险合同的保费。此时，本文将b=T作为最优解也是可以的。

结论三：VaRα(X)≤a时，最优的保险合同形式是免赔额保险。

2.3 最优的一般保险合同

根据上文的分析，在免赔额、赔款上限与VaRα(X)的三种位置关系中，有两种最优保险合同的形式：赔款上限等于VaRα(X)的一般保险合同与免赔额保险合同。但是上文并没有考虑到值的影响，现在考虑值给定的情况下，如何选择在上述两种一般保险合同中选择一种最优形式。

当赔款上限为VaRα(X)时，如果免赔额为0，可以得到：

这是最复杂的一种情况，在这种情况下，赔款上限为VaRα(X)的一般保险合同和免赔额保险合同都是可能的。这里需要比较的是在满足约束条件的情况下，哪种保险合同更加节省保费。但是，现在仍然不能对两种保险合同进行直接比较，因为免赔额保险的免赔额小于VaRα(X)时和免赔额大于VaRα(X)时，自留风险的CTE的计算公式不同，需要进一步分情况讨论。设一般保险合同中的免赔额为a，赔款上限为VaRα(X)；设免赔额保险合同中的免赔额为c。当免赔额保险合同中的免赔额等于VaRα(X)时，有：

这种情况下，满足条件的免赔额保险合同中的免赔额要大于VaRα(X)。两种保险合同的约束条件为：

两种保险合同的保费差为：

不难发现式（19）是一个关于c递减的函数，当c=T时取得最小值。当c=T时，式（19）等于0。这说明，式（19）是大于等于0的，也就是说，N在这个区间内无论取什么值，免赔额保险合同的保费更低。

第一个区间：

此时，免赔额保险合同中的免赔额都要大于VaRα(X)，计算的过程同情况（1）相同。免赔额保险合同的保费更低。

第二个区间：

如果N属于这个区间，说明免赔额保险合同中的免赔额小于等于VaRα(X)。两种保险合同的约束条件为：

两种保险合同的保费差为：

不难说明当 c=VaRα(x)时，式（21）取最小值，但是仍然大于0。因此，式（21）大于0。说明这种情况下，N在这个区间内无论取什么值，免赔额保险合同更加节省保费。

综合以上几种情况，可以得出的结论是：在CTE的约束下，在一般保险合同中，没有上限的免赔额保险合同是最优的。

3 比例保险合同

上文主要分析了最优的一般保险合同，这里将免赔额保险合同与比例保险合同进行比较，研究在CTE的约束条件下，哪种保险合同更加节省保费。比例保险合同，即将风险的一部分进行投保。当发生的损失为X时，保险公司的赔付额为θX，θ为保险比例。因此，在比例保险合同下，投保人的自留风险为(1-θ)X。设免赔额保险合同中的免赔额为c。下面根据N的不同分情况讨论。

在这种情况下，免赔额保险合同中的免赔额小于等于VaRα(X)。免赔额保险与比例保险的约束条件为：

在满足上面的约束条件下，两种保险的保费差为：

整理式（22），可得：

假设在规定的区间内可以随意变动，可以将式（23）看作一个关于N的函数G（N），对G（N）关于N求导，得到：

将式（24）、（25）代入式（26），进行整理，得到：

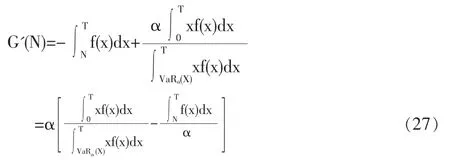
可以证明，G'(N)是一个关于递增的函数，G'(0)＜0，G'(VaR(x))>0。这说明从N=0开始，G（N）开始递减，到达一个最小值后，G（N）开始递增，一直增到 N=VaRα(x)。

当N=0时，c=0，θ=1，也就是投保人全额投保，不自留任何风险，此时 G(N)=0。 当 N=VaRα(X)时，有：

不难证明，式（28）小于0。由以上分析，可以得出结论：在此区间内，G（N）＜0，也就是说，N在这个区间内无论取什么值，免赔额保险都更加节省保费。

这种情况下，免赔额保险中的免赔额大于VaRα(X)，此时，两种保险的约束条件为：

设两种保险的保费差是免赔额的函数：

假设N在规定的区间内可以随意变动，由式（29）左边的等式可知，当N取不同值时，θ时关于c的函数。将等式两边对c求导，得到：

将式（30）对c求导，并将式（31）代入，整理后可以得到：

c≠T时，式(32)明显大于 0，因此 G(c)是关于 c的增函数。当c=T时，说明投保人自己可以承受所有风险，不需要购买保险，此时G(VaRα(X))=0。根据以上分析可知，在这个区间内，G(c)＜0，也就是说，N在这个区间内无论取什么值，免赔额保险都更加节省保费。

综合以上分析，可以得出结论：在CTE的约束条件下，免赔额保险优于比例保险。

4 结论

本文的目的是将投保人的自留风险控制在一定水平下，选择一种最节省保费的保险合同。通过对多种情况分别进行的讨论，本文得出的结论是：在CTE的约束条件下，最优保险合同的形式是免赔额保险。如果仔细思考，这一结论是合理的。CTE只考虑在一定损失水平之上的平均损失，也就是极端情况的平均损失，而不考虑那些发生概率比较大但是金额很低的损失。在比例保费的情况下，所有风险都有相同的价格。因此，合理的作法是为发生概率较小但是损失金额很大的那部分风险进行投保，而对那些发生概率比较大但是金额很低的损失则不投保。这样，既保证CTE处于一个比较小的水平，又可以有效的降低保费。因此，在CTE的约束条件下，免赔额保险应该是投保人的最优选择。这对实际生活中企业或个人的风险管理具有重要的指导意义：投保人在购买保险时，首先要确定自身的风险承受能力，确定自留风险的大小，然后购买相应的免赔额保险。这样，既可以保证将自留风险维持在可承受范围内，又可以使得保费支出最小化。

[1]Arrow,K.J.OptimalInsuranceand Generalized Deductibles[J].Scandinavian Actuarial Journal,1974，1.

[2]Artzner.P.,Delbaen F.,Eber,J.M.,Heath,D.Coherent Measure of Risk[J].Mathematical Finance，1999，9.

[3]Bucay,N.,Rosen,D.CreditRisk ofan InternationalBond Portfolio:A Case Study[J].ALGO Research Quarterly,1999，2(1).

[4]Gollier,C.The Design of Optimal Insurance Contracts without the Nonnegativity Constraint on Claims[J].Journal of Risk and Insurance,1987，54.

[5]Huberman,G.Mayers,D.,Smith,C.W.Optimal Insurance Policy Indemnity Schedules[J].Bell Journal of Economics,1983，14.

[6]Hung-Hsi Huang.Optimal Insurance Contract under a Value-at-Risk Constraint[J].The Geneva Risk and Insurance Review,2006，31.

[7]Jun Cai,Ken Seng Tan.OptimalRetention fora Stop-Loss Reinsurance under the Var and CTE Risk Measures[J].Arstin Bulletin,2007，37(1).

[8]Marry Hardy.An Introduction to Risk Measures for Actuarial Applications[Z].Study Notes，1999.

[9]Pflug,G.Ch.Some Remarks on the Value-at-Risk and the Conditional Value-at-Risk[A].Probabilistic Constrained Optimization:Methodology and Application[C].Kluwer，2000.

[10]Raviv,A.The Design of an Optimal Insurance Policy[J].American Economic Review,1979，69.

[11]Rockafellar,R.T.,Uryasev,S.Conditional Value-at-Risk for General Loss Distributions[J].Journal of Banking and Finance,2002，26.

[12]Uryasev,S.Conditional Value-at-Risk:Optimization Algorithm and Applications[J].Financial Engineering News,2000，14.

[13]Wang,C.P.,Shyu,D.,Huang,H.H.Optimal Insurance Design under a Value-at-Risk Framework[J].The Geneva Risk and Insurance Review,2005，30.