住房抵押贷款保证险的鞅定价与保险精算定价的比较研究

陈丽萍 ，李 晨 ，杨向群

(1.湖南财经高等专科学校 基础课部，长沙 410205；2.湖南农业大学 东方科技学院，长沙 410128；3.湖南师范大学 数学与计算机科学学院，长沙 410081）

1 住房抵押贷款保证险简介

住房抵押贷款保证险(以下简称保证险)包括两种类型：全额担保和部分担保。将抵押贷款期限T划分为n段承保区间，这里仅研究n=1的情形。

1.1 全额担保

若借款人在t=T时刻违约，保险公司可采取以下两种方式履赔：

(1)保险公司向贷款人支付全部未偿贷款余额，并取得房产权由自己实现抵押权。

(2)贷款人保留房屋产权，实现抵押权后，不足以补偿贷款余额的部分由保险公司赔付。

无论哪种方式，保险公司应赔付金额均为：max(M(T)-αH(T)，0)。其中M(T)为T时刻未偿付金额，H(T)为T时刻的房产价格，α为实现抵押权后所得住房价值比例，O为常数。贷款人持有的全额担保保单到期收益为：

1.2 部分担保

保险公司为减少承担的信用风险，只对抵押贷款余额的一定比例实施担保，若借款人在t=T时刻违约，保险公司可采取以下两种方式履赔：

(1)保险公司向贷款人支付全部未偿贷款余额，并取得房产权由自己实现抵押权。赔付额为max(M(T)-αH(T)，0)。

(2)向贷款人赔付所担保比例的贷款额，银行仍保留房屋产权。赔付额为：γM(T)，其中γ代表承保比例。此时，贷款人持有的部分担保保单到期收益为：

2 数理金融模型的建立

考虑连续时间的金融市场，时间区间为[0，T]，0表示现在，T表示到期日。给定某完备概率空间(Ω，F，P)。设了时刻的未偿付额M(T)=M为常数(可由风险信用评估得到)，无风险利率为常数r，房产价格为H(t)满足如下随机微分方程：

其中，B={B（t）}0≤t≤T是定义在完备概率空间(Ω，F，P)上的标准布朗运动，(Ft)0≤t≤T为相应的自然信息流，Ft=F。 μ，a，σ 为常数，且 a＞0，σ＞0。

引理1[5]设房产价格满足式(1)，则有

3 两类保证险的鞅定价

设市场完备、无套利，则可用鞅方法获得保证险的无套利定价。

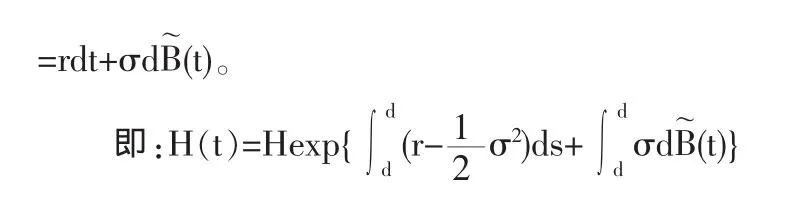
定理1 设市场完备、无套利，承保期为[0，T]，到期现金流满足式(1)，无风险利率为常数r，未偿付额恒为常数M，房格H(t)满足式(1)，则全额担保保证险的鞅定价公式(保费)为

综上，定理得证。

定理2 设市场完备、无套利，承保期为[0，T)，到期现金流满足式(2)，无风险利率常数r，未偿付额恒为常数M，房产价格H(t)满足式(3)，则部分担保保证险的鞅定价公式(保费)为

综上，定理得证。

4 两类保证险的保险精算定价

定义 2 设 C（K，T）和 P（K，T）分别表示标的风险资产价格为H（t），执行价格为K，到期日为T的欧式买权和卖权在现在时刻的价值，则

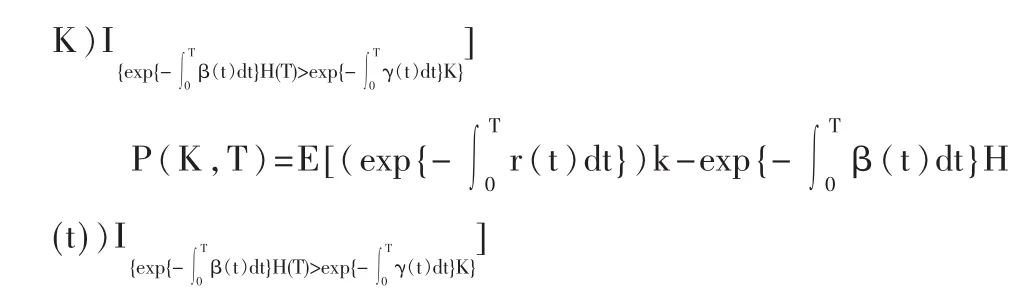
这一定价方法称为期权的保险精算定价方法。

定理3 设承保期为[0，T]，到期现金流满足（1），无风险利率为常数 r,未偿付额恒为常数 M，房产 H（t）满足（3）,则金额担保保证险的保险精算定价（保费）为

综上，定理得证。

定理 4 承保期为[0，T]，到期现金流为(2)，未偿付额恒为常数M，房产价格H(t)满足(3)的部分担保保证险的保费为

下面将分别给出上式中三项期望的值。由于η～N(0，1)，于是有

综上，定理得证。

5 两种定价结果的比较

本文引入期权定价思想，分别利用传统的鞅定价方法和保险精算定价方法，探讨了两类住房抵押贷款保证险的定价问题，并且分别给出了两种方法下保证险的定价公式。

将定理1与定理3、定理2与定理4进行对比，可以看出：在相同的市场模型下，保险精算定价和传统的鞅定价(又称无套利定价)有明显区别。当房产价格服从指数O-U过程时，保险精算定价与房产预期收益率非线性漂移系数α和波动率σ有关，无套利定价仅与波动率σ有关，而与预期收益率无关。由于等价鞅测度存在且唯一，所以保证险有唯一的无套利定价，因此这里的保险精算定价实质上是有套利定价。

可见，当房产价格服从一般的随机过程时，保险精算方法给出的保证险定价与传统的鞅方法给出的定价(无套利定价)可能是不一致的。虽然用保险精算方法也能证明B-S公式，但对一般的风险资产价格模型，其定价可能是有套利的。

[1]侯新华，田策.住房抵押贷款保证险研究[J].中国房地产金融,2002，(11).

[2]钱乃余.发展我国住房抵押贷款保险之构想[J].济南金融,200l，(6).

[3]陈丽萍，杨向群.房价服从非时齐Poisson住房抵贷款保证险的定价[J].应用概率统计,2007,23(4).

[4]李晨，陈丽萍，杨向群.随机波动率与跳扩散相结合的保证险的鞅定价[J].系统工程，2009,27(3).

[5]闫海峰，刘三阳.广义Black-Scholes模型期权定价新方法保险精算方法[J].应用数学和力学,2003,24(7).