双边密封竞标下的动态P2P网络借贷拍卖机制
周正龙,马本江,胡凤英
(中南大学商学院,湖南长沙410083)
1 引 言
早在公元前500年,拍卖就被用于出售各种物品.无论是艺术品还是古董,都会在拍卖会上落槌卖出.现在的许多商品(比如烟草、鱼、鲜花、废金属等)都可以通过拍卖的方式进行交易,甚至于一些公用事业的债券也可以通过拍卖出售给投资公司.而在当今时代,不同市场的拍卖机制逐渐被细分,不同领域逐渐形成自己的拍卖版式.例如,在采购市场中,通常采取数量拍卖(quantity auction)、供应合同拍卖(supply contract auction)进行交易[1,2],在考虑多属性的情形下,也会采取(或改进)第一评分拍卖(first score auction)、第二评分拍卖(second score auction)进行交易[3,4].因此,在中国P2P(peer-to-peer)网络借贷市场中,简单地复制这些拍卖机制并不能有效解决P2P网络借贷问题,无法使得资源配置达到帕累托最优状态.进一步地,中国P2P网络借贷市场存在较大的风险,很多贷款人(资金提供者)在进行投资的过程中常常会存在羊群效应、聚集效应和菱镜效应[5],从而会加大市场风险.在不完全信急背景下,中国P2P网络借贷市场还可能出现套利交易(即借入后再借出进行投资以获得利急差)、暗箱操作(即P2P借贷变为P2P暗箱投标)等影响交易正常运行的不良行为,这些行为有可能导致市场失灵.所以,有必要对贷款人和借款人(资金需求者)的交易机制进行详细研究.
目前国外文献主要集中于信用风险等相关问题的实证研究[6−8].同样地,国内文献也主要侧重于风险控制、平台发展、资产定价等问题的实证研究[9−11],较少涉及P2P网络借贷交易机制方面的理论研究.仅少数学者从拍卖的角度说明了竞标方式比文字描述更好解决P2P借贷问题,竞标方式能够更好地披露借款人信急,激励借款人在还款过程中履行借款约定,有良好信誉记录的借款人能够获得更低成本的借款[12].从实际情况来,一些P2P网络借贷平台也使用拍卖方式进行交易.例如,Prosper,Funding Circle和Innovestment等都是关注拍卖交易的典型平台.这些平台的主要交易模式是贷款人之间自行竞拍,通过贷款人拍卖确定借贷利率(2010年之前Prosper一直采用拍卖机制).因此,基于已有P2P借贷拍卖模式和第三方交易平台的双边市场特征[13],提出一种双边密封竞价的动态关闭式拍卖机制(简称双边密封拍卖机制).相对于已有P2P借贷拍卖机制[14,15],这个机制最突出的特点是同时考虑了贷款人和借款人的报价,使得借款人和贷款人在一定程度上把握了借贷的自主权.进一步地,该机制是在密封报价的模式下进行的,有利于规避贷款人的羊群效应.此外,与中国目前较多采取借款人事前定价的机制相比,这类拍卖机制有利于激化贷款人之间的竞争,激励贷款人报告自己的真实类型,可以对中国P2P网络借贷机制的创新提供一定的启示.
双边密封拍卖提供了两种情形下的模型.第一种情形(基准模型)是基于不完全密封约束得到的,即借款人和贷款人的报价属于事前密封信急,而贷款人提供的资金数额(简称为配额)是所有贷款人共同知道的信急.第二种情形(拓展模型)是基于完全密封约束得到的,即借款人和贷款人的报价、配额都属于事前密封信急.此外,对不同模型提供了不同的拍卖策略.当然,由于基准模型中的配额是所有贷款人共同知道的信急,因此贷款人在基准模型的拍卖机制中可以学习或模仿其他贷款人的决策,即贷款人之间可以通过配额推测其相应报价信急,进而会预想到所有贷款人的拍卖策略.所以,在不完全密封的关闭式拍卖中,虽然可以得到所有贷款人的真实报价构成纳什均衡解,满足激励相容性.但是贷款人之间的羊群行为会增加借贷交易的支付成本[16],因此可以将基准模型进一步拓展到完全密封的情形,以进一步减少羊群行为对P2P网络借贷交易机制的影响.通过数值算例的分析也表明,双边密封竞价的动态关闭式拍卖从一定程度上可以制约贷款人的决策,有利于改进借款人的支付水平.
2 基准模型:不完全密封拍卖
2.1 拍卖模型及性能分析
在基准模型中,设定贷款人提供的配额是根据其余竞争贷款人的供给自行决定的(即当前配额是其他贷款人所知的),贷款人可以模仿或学习其他贷款人的行为.因此,将基准模型定义为不完全密封拍卖.下面用数学语言对基准模型加以描述.这里先给出几个背景假设:1)在整个拍卖的过程中不存在P2P平台商的监管套利问题.2)P2P网络借贷平台能够有效监管借贷行为,保证拍卖机制的正常执行.现设定借款人的借款需求为D,在任意t时刻的报价为P(t),这个价格对所有参与竞标的贷款人是事前密封的,满足并且设定在第三方平台事先规定的范围内,属于借贷双方的共同知识[17].进一步假设n个贷款人L1,L2,...,Ln参与竞标,并且在拍卖结束之前竞标报价是事前密封的(即所有潜在的贷款人不知道其他贷款人提供的报价信急).同时假设,任意一个贷款人Li参与竞标并带有一个真实的私人利率ri(t),i={1,2,...,n},ri(t)一般等价于贷款人Li最佳外部选择的利率(0贷款人Li在任意t时刻参与拍卖竞标的报价为bi(t),并且提供的配额为ai(t),其中这样便可以定义,n个贷款人L1,L2,...,Ln在任意t时刻参与拍卖的报价集合和配额集合分别为B(t)={b1(t),b2(t),...,bn(t)}和A(t)={a1(t),a2(t),...,an(t)},满足t=1,2,...,T.T表示拍卖规定的时间,T∈N∗,N∗是正整数集合.此外,规定借款人的借款需求D和配额ai(t)都是整数,并且属于共同知识.这里需要强调的是,双边密封竞价主要指借款人和贷款人的报价都是事前密封的.
借款人向所有候选的贷款人宣布拍卖规则:首先,借款人宣布一个借款合同{D,Vi(t)},这个合同包含了借款需求D、借款人的密封报价P(t)以及定价函数Vi(t)=bi(t)+λ(P(t)−bi(t))(这里设定定价函数满足“小中取大、大中取小”的约束条件,即对bi(t)≤P(t)的贷款人,取最大报价的贷款人为这类贷款人的有效报价;对bi(t)>P(t)的贷款人,取最小报价的贷款人为这类贷款人的有效报价).随后,贷款人Li从任意时间点t=1,2,...,T根据借款合同{D,Vi(t)}报出愿意供给的配额和报价,并且第三方平台按照“小中取大、大中取小”的约束条件来确定拍卖价格Vi(t)和有效借款配额数此时,如果得到的有效借款数额那么宣布拍卖结束,并公布借款人和所有中标贷款人的报价信急;否则,任意的贷款人Li进入下一个时间点报出愿意供给的配额和报价;如此重复,直到有效借款数额时宣布拍卖结束.最后,如果得到的有效借款数额就以流标方式结束,所有的配额通过第三方平台退回贷款人,并宣布拍卖结束.
定义1对于满足上述规则的任意P2P网络借贷拍卖,如果同时满足关闭式拍卖的约束条件,就可以称为动态的双边密封关闭式拍卖,简称双边密封拍卖(D-DCA).
宣布这个规则后,借款人按如下过程执行这个拍卖机制:1)借款人设定具体的竞拍时间T,并且宣布一个借款合同{D,Vi(t)}至指定的第三方平台,其中定价函数Vi(t)=bi(t)+λ(P(t)−bi(t)),并且满足上述“小中取大、大中取小”的约束条件.2)所有贷款人被邀请或自愿参加拍卖.如果在规定时间内没有贷款人愿意报出任意的配额ai(t)和报价bi(t),宣布拍卖结束,没有发生交易.否则,在拍卖给定定价Vi(t)时,中标贷款人获得借款人提供的子合同{ai(t),Vi(t)}.3)重复步骤2)直到时间达到T时,如果所有成功竞拍的贷款人提供的有效配额就以成功方式宣布拍卖结束,借款人提供给每个中标贷款人相应的子合同{ai(t),Vi(t)},t=1,2,...,T,并附上还款期、还款方式等相关的材料.4)如果在规定时间内所有成功贷款人的有效配额就以流标方式结束拍卖.
相对于Chen等[14]设计的动态Prosper拍卖而言,D-DCA机制最主要的突出特征是进一步考虑了借款人的报价,使得借款人在一定程度上把握了借贷的自主权;同时以合同的方式结束拍卖,体现了法律上的保护权益.设计这个机制的动机也是为了降低借款人的支付成本,减少贷款人在拍卖过程中的羊群效应[16].为了验证这些结果,先给出如下的定义.
定义2给定k=min=2,3,...,T,m=1,2,...,n,满足b1(s)≤b2(s)≤···≤bm(s)),当i≤k时,贷款人Li在时间点s的配额为ai(s),ak(s)=当i>k时,贷款人Li在时间点s的配额为0.那么称Lk为最后一个成功的贷款人,称Lk+1为最早一个失败的贷款人.特别地,当s=1时,k=min
进一步地,给定t=1,2,...,T,B(t)={b1(t),b2(t),...,bk(t)},当满足≤ P(t) 时,定价函数为Vi(t)=当满足> P(t) 时,定价函数为Vi(t)=当满足j个贷款人的报价小于或等于P(t),k−j个贷款人的报价大于P(t)时(1≤j≤k),定价函数为

得到最后一个成功的贷款人和拍卖定价之后,根据拍卖的执行过程给出具体的计算:当t=1时,如果满足D,那么拍卖继续直至下个时间点上不存在多余的供给,此时拍卖的截止时间t=1,且最后一个成功的贷款人Lk的配额为ak(1)=满足=D;反之,进入下一个时间点t=2.当t=2时,如果满足=ai(2)≥ D,那么拍卖的截止时间t=2,并且最后一个成功的贷款人Lk的配额为ak(2)=D−满足=D;反之,进入下一个时间点t=3.如此进行,在规定时间内,如果存在时间点s=2,3,...,T满足那么时间点s为拍卖的截止时间,此时得到最后一个成功的贷款人Lk的配额为ak(s)=D−并且满足=D.反之,如果不能满足≥D,那么说明在规定时间内无法使得贷款供给大于等于借款需求,拍卖视为失败,配额通过第三方平台退回贷款人,拍卖结束.
得到D-DCA机制之后,需要分析其是否满足激励相容性,具体如命题1所示.
命题1对定义1中的任意D-DCA机制,如果存在时间点s=2,3,...,T 满足k个贷款人成功参与竞标,即那么D-DCA机制满足激励相容性.(证明见附录1)
下面,进一步分析激励相容的D-DCA机制的均衡解,同时考虑贷款人和借款人之间的逆向选择问题(即考虑借款人违约的概率),分析可能存在的均衡解扭曲问题.这里假设借款人的违约概率与定价函数存在某种函数关系,让δ(Vi(t))表示给定Vi(t)下的违约率,满足δ′(Vi(t))≥ 0.同时,设定一个贷款人认为提供贷款是有利可图的条件是当且仅当1+ri(t)≤(1+Vi(t))(1−δ(Vi(t))),可以简化为ri(t)≤ Vi(t)−(1+Vi(t))δ(Vi(t)).让 γ(Vi(t))=Vi(t)−(1+Vi(t))δ(Vi(t)),表示贷款的期望回报率.据此,可以通过命题2对D-DCA机制的均衡解加以描述.
命题2对于任意激励相容的D-DCA机制,如果存在时间点s=2,3,...,T,满足k个贷款人成功参与竞标,即并且满足提供贷款是有利可图时,所有成功参与竞标的贷款人的真实报价和配额构成纳什均衡解.(证明见附录2)
通过命题2发现,对于任意激励相容的D-DCA机制而言,如果借贷交易成功,那么所有成功参与竞标的贷款人的真实报价和配额构成纳什均衡解,并且借款人的违约率会影响整个机制的均衡状态.事实上,借款人的违约率对贷款人提供贷款的概率产生显著影响,即当1+ri(s)>(1+Vi(s))(1−δ(Vi(s)))时,贷款人不会提供贷款(贷款人会事后违约).此时,所有贷款人不参与竞标,进而导致市场不存在,因此激励相容的D-DCA机制也就不存在纳什均衡状态.所以,借款人的违约率会影响整个机制的均衡状态,并且当借款人的违约率不可观测时,贷款人的事后违约也会导致拍卖机制失灵.
最终结合命题1和命题2指出,激励相容的D-DCA机制存在的充分条件是贷款人所提供的贷款是有利可图的,即满足1+ri(s)≤(1+Vi(s))(1−δ(Vi(s))).因此,主要从贷款人的角度去设计拍卖机制,从贷款人追求期望收益最大化角度去研究拍卖机制.
2.2 拍卖策略分析
结合以上分析,进一步探讨D-DCA机制中有关借款人和贷款人的最优拍卖策略.根据定价函数Vi(t)=bi(t)+λ(P(t)−bi(t))中的激励或惩罚系数λ来确定不同情形下的拍卖策略.
情形1当λ=0时,借款人和所有成功贷款人的最优拍卖策略均以的报价参与拍卖,并且获得最优定价为满足
当λ=0时,Vi(t)=bi(t)+λ(P(t)−bi(t))=bi(t),说明竞价策略完全取决于所有贷款人的报价.所以对于所有理性的贷款人而言,选择以的报价参与拍卖无疑是最优的.这是因为,当λ=0时,对于所有小于等于借款人报价P(t)的贷款人而言,最终定价为对于所有大于借款人报价P(t)的贷款人而言,最终定价为满足因此取时,贷款人获得局部最优的报价,这样就可以进一步得到最终的定价为进一步地,借款人在设定λ=0时也已经预想到所有成功贷款人的拍卖策略是以的报价参与拍卖,所以借款人的最佳响应策略也将是以的报价参与拍卖,这样可以有效规避期望损失.此外,值得关注的是,λ=0情形下的策略类似于Prosper动态拍卖机制的竞价策略,即由贷款人竞价决定最终的交易利率.由此可见,当λ被0替代,被0替代(对于i=j+1,j+2,...,k,bi(t)>P(t))时,Prosper动态拍卖机制是D-DCA机制的一个特例.
情形2当λ=1时,所有成功贷款人的最优拍卖策略是以的报价参与拍卖,并且这个报价是借款人提供的,所以最优定价为
当λ=1时,Vi(t)=bi(t)+λ(P(t)−bi(t))=P(t),说明这时候的竞价策略取决于借款人的报价P(t),与贷款人的报价无关.进一步地,按照式(1)的解释意义不难得到,不管所有贷款人的报价是小于等于借款人报价还是大于借款人报价,拍卖的最终定价为P(t),满足此时,λ=1情形下的策略等价于拍拍贷撮合机制的竞价策略,即借款人给定一个借款需求D,并提供一个的最小值,随后通过平台发布信急;所有潜在的贷款人以报价参与竞标,并且不再提供任何报价;最后如果竞拍成功,借款人以借款利率或报价提供相应的支付.进一步得到,拍拍贷撮合机制也是DCA机制的一个特例,即λ被1替代.
情形3当0<λ<1时,所有成功贷款人的最优拍卖策略是以的报价参与拍卖,借款人的最优拍卖策略是以的报价参与拍卖,并且获得最优定价为
根据式(1)得到,0<λ<1情形下的竞价策略主要取决于借款人和贷款人报价组合{P(t),bi(t)},并且满足进一步地,当借款人和贷款人报价组合{P(t),bi(t)}取任意数值时,不难得到,由此可见,对于理性的贷款人而言,选择一个大于借款人报价的策略无疑是占优的,但是具体的策略也需要依赖于借款人的报价,所以在无法确定借款人报价的前提下,贷款人选择是局部最优的.因为Vi(t)=是一个增函数,因此取时,贷款人获得局部最优的定价.这样就可以得到最终定价为进一步地,借款人在设定0<λ<1时也已经预想到所有成功贷款人的拍卖策略是以的报价参与拍卖,所以借款人的最佳响应策略也是以的报价参与拍卖,因为关于报价P(t)是一个增函数,因此取时,借款人能获得局部最优的定价.
情形4当λ>1时,借款人和所有成功贷款人的最优拍卖策略是以的报价参与拍卖,并且获得最优定价为
同理,根据式(1)得到λ>1情形下的竞价策略主要取决于借款人和贷款人报价组合{P(t),bi(t)},并且满足但是当{P(t),bi(t)}取任意值时,容易得到

由此可见,对于理性的贷款人而言,选择一个小于或等于借款人报价的策略无疑是占优的,但是具体的策略也需要依赖于借款人的报价,所以在无法确定借款人相关报价信急的前提下,贷款人选择是局部最优的.这是因为是一个减函数,因此取时,贷款人获得局部最优的报价.这样就可以进一步得到最终的定价为进一步地,借款人在设定λ>1时也已经预想到所有成功贷款人的拍卖策略是以的报价参与拍卖,所以借款人的最佳响应策略也是以的报价参与拍卖,因为关于报价P(t)是一个增函数,因此取时,借款人能获得局部最优的定价.
结合情形1至情形4的分析,有如下结论.
结论1在不完全密封情形下,任意成功贷款人能通过最优拍卖策略实现收益最大化.其中,当λ=0时,借款人和所有成功贷款人的最优拍卖策略均以的报价参与拍卖,满足当 λ =1 时,所有成功贷款人的最优拍卖策略是以借款人的报价参与拍卖;当0<λ<1时,所有成功贷款人的最优拍卖策略是以的报价参与拍卖,借款人的最优拍卖策略是以的报价参与拍卖;当λ>1时,借款人和所有成功贷款人的最优拍卖策略是以的报价参与拍卖.
值得注意的是,结论1属于完美定价状态.在实际的运行过程中,借款人可能会结合借款需求的紧迫性等适当抬高报价,以增加密封报价的随机性;同时,牺牲部分收益以获得密封报价随机性的行为也有利于保持D-DCA机制的双边叫价特征,有利于保持贷款人之间的相对独立性,而不至于产生借贷双方的套利交易行为.除此之外,在实际运行过程中,也会存在非理性的贷款人成功参与D-DCA机制,并且非理性贷款人在D-DCA机制中可以模仿其他贷款人的决策(羊群效应).所以,可以将基准模型进一步拓展到完全密封的情形,以减少羊群效应对P2P网络借贷拍卖机制的影响.
3 拓展模型:完全密封拍卖
3.1 拍卖模型及性能分析
在拓展模型中,给定每个贷款人提供的配额不构成其他贷款人的共同知识,无法学习或模仿其他贷款人的行为决策.这种完全密封的关闭式拍卖类似于不完全信急下的密封拍卖模式,只是P2P网络借贷交易机制中的拍卖模式属于关闭式拍卖,因此不能直接采用不完全信急下的密封拍卖模式,但是不完全信急下的密封拍卖也说明了这种拍卖对于借款人是最优的.
为了区别于不完全密封竞价情形,这里做如下几点假设:1)借款人的借款需求D带有一个保留利率R.保留利率R可以理解为,借款需求D在实际经营过程中预期得到的边际收益率,它表明一个投资项目的收益应按何种比例增长才能达到预期的收益,因此,它也代表了借款人通过借款需求D进行投资而获得的边际利润率;2)在拍卖结束之前,贷款人的竞标报价和配额都是事前密封的.这里可以将贷款人的报价和配额组合为φi(t)=(bi(t),ai(t)),并以ϕi(t)参与拍卖.这样便得到n个贷款人L1,L2,...,Ln在任意t时刻的投标集合为Φ(t)={φ1(t),φ2(t),...,φn(t)},其中t=1,2,...,T;3)完全密封情形的拍卖规则类似于不完全密封情形,只是将定价函数设为Vi(t)=φi(t)+λ(P(t)−φi(t)).
所以,相对于基准模型而言,拓展模型最主要的突出特征是进一步考虑了贷款人相关配额的密封性,使得贷款人在投资决策过程中无法推测其他贷款人的投标信急,保证借贷双方真实披露各自的私人信急.对比基准模型发现,拓展模型的定价函数由Vi(t)=bi(t)+λ(P(t)−bi(t))变为Vi(t)=φi(t)+λ(P(t)−φi(t)).所以,先给出拓展模型的相关定义.
定义3对于满足定义1的任意P2P网络借贷拍卖机制,如果能够将Vi(t)=bi(t)+λ(P(t)−bi(t))变换为Vi(t)=φi(t)+λ(P(t)−φi(t)),就可以被称为双边完全密封拍卖(简称CD-DCA).
定义4给定= 2,3,...,T,m= 1,2,...,n,满足 φ1(s)≤ φ2(s)≤ ···≤ φm(s),当 i≤ k时,贷款人 Li在时间点 s的配额为 ai(s),ak(s)=D −当i>k时,贷款人Li在时间点s的配额为0.那么称Lk为最后一个成功的贷款人,称Lk+1为最早一个失败的贷款人.特别地,当s=1时,k=min
进一步地,给定 t=1,2,...,T,Φ(t)={φ1(t),φ2(t),...,φk(t)},当成立时,定价函数为当满足时,定价函数为当满足j个贷款人的报价小于或等于P(t),k−j个贷款人的报价大于P(t)时(1≤j≤k),定价函数为
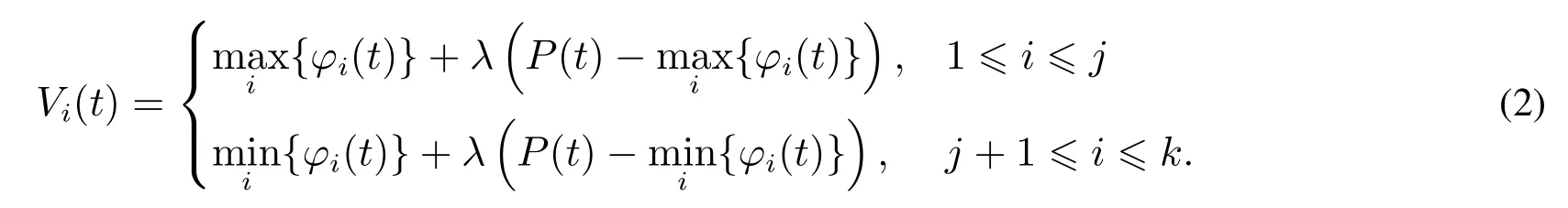
得到拓展模型的定价函数和分配规则之后,给出拍卖的执行过程:在规定时间内,如果存在时间点s=2,3,...,T满足≥D,那么时间点s为拍卖的截止时间,这时得到最后一个成功的贷款人Lk的配额为ak(s)=D−并且满足=D.反之,如果不能满足D,那么说明在规定时间内无法使得贷款供给大于等于借款需求,拍卖视为失败,配额通过第三方平台退回贷款人,拍卖结束.
对拓展模型的激励相容性,有下列结论.
命题3对定义3中的任意CD-DCA机制,如果存在时间点s=2,3,...,T满足k个贷款人成功参与竞标,即那么所有贷款人的真实竞标构成纳什均衡解,并且满足激励相容特征.(证明见附录3)
命题3同样说明了,在贷款人成功参与拍卖时,任意的CD-DCA机制是满足激励相容特征的,并且所有成功贷款人的真实竞标构成纳什均衡解.进一步地,在考虑借款人违约率的情形下,可以得到与命题2一致的结果,即只要满足贷款人提供贷款是有利可图的,那么CD-DCA机制也是激励相容的(这里不再单独展开证明过程),同时说明了借款人的违约率会影响整个机制的均衡状态.反之,当贷款人提供贷款不是有利可图的,贷款人不会提供贷款(贷款人会事后违约),那么CD-DCA机制会失灵.所以,从借款人违约的角度考虑,命题3的结论与命题2相似,即激励相容的CD-DCA机制存在的充分条件是贷款人所提供的贷款是有利可图的.差异性在于,命题3是基于完全密封的状态下进行的,不存在贷款人的模仿和学习策略.
3.2 拍卖策略分析
为了进一步探讨CD-DCA机制的拍卖策略,假设组合(bi(t),ai(t))具有相同的分布函数F和密度函数f.其中F(·|ai(t))和f(·|ai(t))分别表示为贷款人在配额为ai(t)时的条件分布函数和密度函数.
因此,令
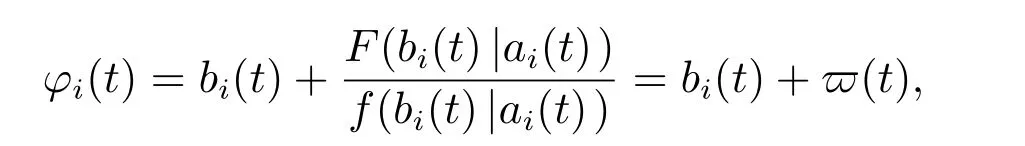
同时对于所有的ai(t),φi(t)关于bi(t)是非减的,对于所有的bi(t),φi(t)关于ai(t)是非增的[18,19].下面根据定价函数Vi(t)=φi(t)+λ(P(t)−φi(t))中的激励或惩罚系数λ来确定不同情形下的拍卖策略.
情形5当λ=0时,任意成功贷款人的最优策略为并且满足此时的最终定价为
当λ=0时,Vi(t)= φi(t)+λ(P(t)−φi(t))= φi(t),说明这时候的竞标策略完全取决于贷款人Li的竞标组合φi(t)=(bi(t),ai(t)).设ui(φi(t))=ai(t)(Vi(t)−ri(t))表示贷款人Li的利润函数(为了简化,这里不考虑违约率的影响).所以对于理性的贷款人Li而言,ui(φi(t))=ai(t)(Vi(t)−ri(t))=ai(t)(bi(t)+ϖ(t))−ai(t)ri(t),此时结合不难得到ui(bi(t),ai(t))的最大值.不妨假设是 ui(φi(t))取最大值的点,这样就可以得到 λ =0 情形下贷款人Li的最优竞标策略是所以,在任意t时刻,任意成功贷款人的最优策略为这也说明了,λ=0情形下的所有贷款人无法推测其他贷款人的拍卖策略,所以贷款人的最佳响应策略是最大化ui(φi(t)),这样可以从一定程度上规避贷款人之间的羊群效应.最终得到定价为
情形6当λ=1时,任意成功贷款人的最优策略是以的竞标参与拍卖,但是这个竞标是借款人提供的,所以最优定价为
当λ=1时,Vi(t)=φi(t)+λ(P(t)−φi(t))=P(t),说明此时的竞标策略取决于借款人的报价P(t),与贷款人的竞标组合无关.
一方面,ui(φi(t))=ai(t)(Vi(t)−ri(t))=ai(t)P(t)−ai(t)ri(t),又因为所以ui(φi(t))=ai(t)P(t)−ai(t)ri(t)≥0,此时贷款人也无法推测其他贷款人的拍卖策略,其最佳响应策略是最大化自己的配额,即耗尽自己的预算配额或提供自己的真实配额.
情形7当0<λ<1时,任意成功贷款人的次优策略是以的报价参与拍卖,借款人的次优策略是以的报价参与拍卖,并且获得最优定价为
当0<λ<1时,任意贷款人的竞标策略主要取决于借款人和贷款人报价组合{P(t),φi},满足
情形8当λ>1时,借款人和任意成功贷款人的次优策略是以的报价参与拍卖,并且获得最终的定价为
当λ>1时,同样给出,任意贷款人的竞标策略主要取决于借款人和贷款人报价组合{P(t),φi},满足
因为 ui(φi(t))=ai(t)(1− λ)(bi(t)+ϖ(t))+ai(t)(λP(t)−ri(t)),0<ai(t)≤D,此时无法确定借款人报价信急,因此不能根据约束条件得到ui(bi(t),ai(t))的最大值.贷款人只能结合函数φi(t)关于bi(t)的非减性质取时,贷款人实现次优策略.即任意成功贷款人的次优策略是以的报价参与拍卖.
结合情形5至情形8的分析,有如下结论.
结论2在完全密封的情形下,任意成功贷款人能通过相应拍卖实现最优或次优策略.其中,当λ=0时,任意成功贷款人能通过实现最优策略;而当λ> 0时,任意成功贷款人只能通过的报价或者通过的报价参与拍卖,实现次优策略,说明λ>0情形下的拍卖机制使得贷款人的策略向下扭曲,小于最优水平值.
结论2主要说明了完全密封竞标情形的拍卖策略在λ>0情形下被扭曲,使得贷款人无法直接获得最大化的收益或利润,同时也验证了这种拍卖机制可以从一定程度上制约贷款人的决策,有利于降低借款人的成本.进一步地,λ=0或者λ>0情形下的拍卖机制能保证所有贷款人无法推测到其他贷款人的拍卖策略,所以,贷款人的最佳响应策略是最大化自己收益或者局部优化自己的收益,而不是依靠其他贷款人的竞标信急.因此,这样的机制可以从一定程度上规避贷款人之间的羊群效应,使得所有贷款人能尽量根据自己的实际情况做真实的决策.
4 算例分析与比较
下面通过数值算例说明所设计拍卖机制的执行过程.由于篇幅有限,仅仅考虑D-DCA机制的拍卖策略和支付情况:假设借款人设定具体的竞拍时间为T=6 d,并且在t0=1 d内宣布一个借款合同{500,Vi(t)}至指定P2P网络借贷平台,其中Vi(t)=bi(t)+0.5(P(t)−bi(t)),定价函数满足“小中取大、大中取小”的约束条件.进一步设定,借款人的借款需求为D=500元,借款人提供的密封报价保持不变,即P(1)=P(2)= ···=P(T)=0.1,并且满足P(t)∈[0.05,0.15].随后,借款人邀请具有闲置资金的所有贷款人进入指定P2P平台参加这个D-DCA拍卖;并且在任意时间段内的n个贷款人提供各自的配额ai(t)和报价bi(t).进一步地,在整个拍卖结束时获得所有成功参与的贷款人数为6人,分别为L1,L2,...,L6,对应的拍卖策略如表1所示,L6为最后一个成功的贷款人,并且不考虑借款人违约情况.按照式(1)可以计算出所有中标贷款人的定价函数,具体如表2所示.
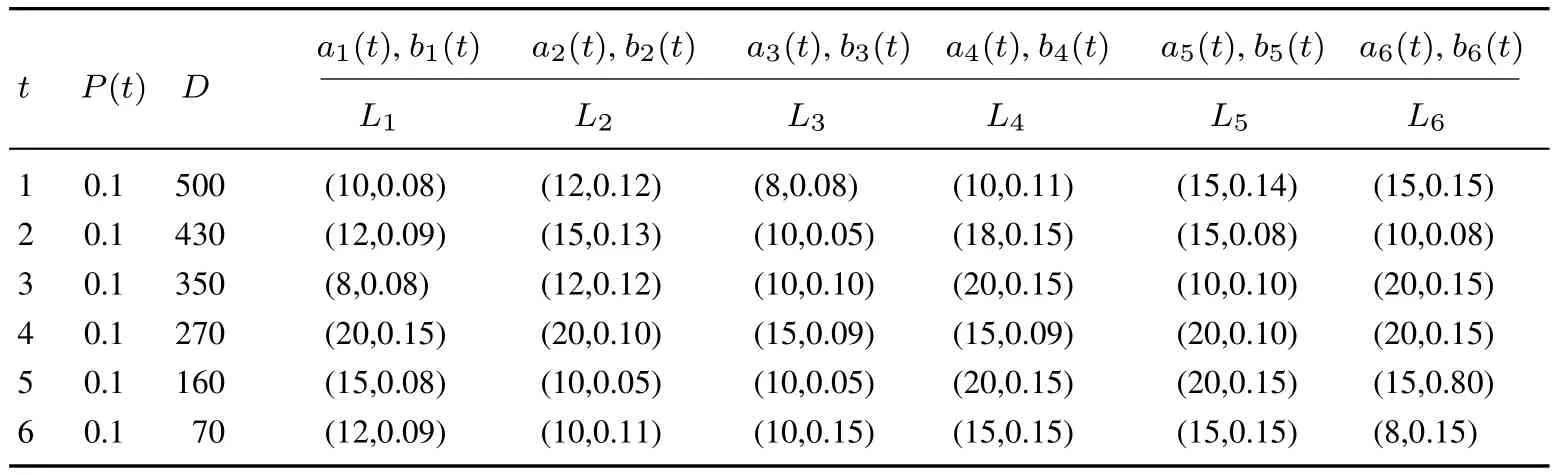
表1 所有成功贷款人的投标组合Table 1 All successful lenders’bid combinations
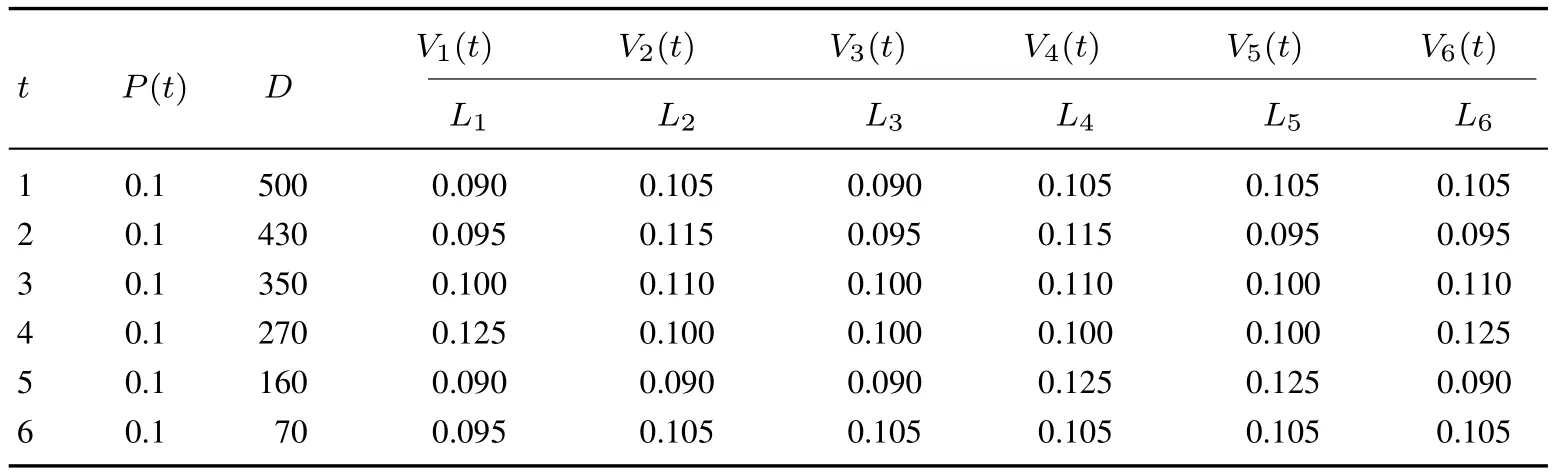
表2 λ=0.5情形下的定价函数Table 2 The pricing function in the case of λ=0.5
对比不同机制的结果得到,算例中的D-DCA机制的拍卖策略(λ=0.5)优于Prosper的拍卖机制(λ=1),弱于拍拍贷的撮合机制(λ=0),因为D-DCA机制的支付水平介于拍拍贷的撮合机制和Prosper的拍卖机制之间(Y(P(t),ai(t))≤Y(Vi(t),ai(t))≤Y(bi(t),ai(t))),其中拍拍贷的撮合机制相当于λ=0情形下的D-DCA机制,Prosper的拍卖机制相当于λ=1情形下的D-DCA机制,这也说明了D-DCA机制的支付水平是随着λ的变化而变化的(站在借款人的角度去比较不同情形之间差异性).
特别地,当0≤λ≤1时,D-DCA机制的支付水平是随着λ的增大而增大的.为了进一步研究D-DCA机制的支付水平在λ>1情形下的变化情况,假设定价函数Vi(t)=bi(t)+2(P(t)−bi(t)),并满足“小中取大、大中取小”的约束条件.同样按照公式(1)得到所有贷款人的定价函数,具体如表3所示.

表3 λ=2情形下的定价函数Table 3 The pricing function in the case of λ=2
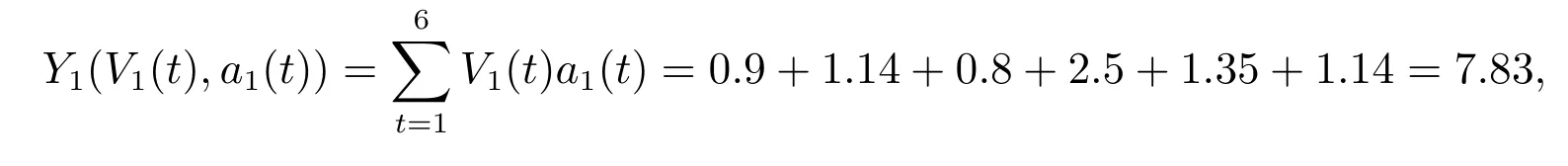
结合表1和表2得到,借款人给贷款人L1的总支付给贷款人L2的总支付Y2(V2(t),a2(t))=8.255,给贷款人L3的总支付Y3(V3(t),a3(t))=6.12,给贷款人L4的总支付Y4(V4(t),a4(t))=10.895,给L5的总支付Y5(V5(t),a5(t))=10.075,给贷款人L6的总支付Y6(V6(t),a6(t))=9.415.进一步将所有贷款人的支付加总就可以得到借款需要支付的所有费用.当然,这里的支付费用不包括贷款人的本金,所以借款需要支付的所有费用等价于借款总共需要支付的利急.于是得到Y(Vi(t),ai(t))=52.59.此时,如果按照拍拍贷的撮合机制,即按照借款人的统一报价P(1)=P(2)=···=P(T)=0.1,同样可以给出借款需要支付的所有利急为Y(P(t),ai(t))=DP(t)=50.如果按照Prosper的拍卖机制,即按照贷款人各自的报价参与拍卖,同样可以给出借款需要支付的所有利急为Y(bi(t),ai(t))=bi(t)ai(t)=57.56.
结合表1和表3得到,借款人给贷款人L1的总支付

给贷款人L2的总支付=7.865,给贷款人L3的总支付=6.66,给贷款人L4的总支付=8.42,给L5的总支付=8.35,给贷款人L6的总支付=7.57.进一步将所有贷款人的支付加总就可以得到借款需要支付的所有费用.于是得到=46.305.这说明,算例中的D-DCA机制的拍卖策略(λ=2)优于拍拍贷的撮合机制(λ=0)和Prosper的拍卖机制(λ=1),因为此时的支付水平明显小于拍拍贷撮合机制和Prosper拍卖机制的支付水平所以,当λ>1时,D-DCA机制的支付水平是随着λ的增大而减小的.
5 结束语
目前中国很多P2P网络借贷平台只考虑借款人的报价,使得这类拍卖机制无法获知贷款人行为信急,并且在实际运行中容易失灵或增加借款人的支付成本.因此设计了一种双边密封竞价的动态关闭式拍卖(简称双边密封拍卖),并提供了两种不同情形下的模型.其中,第一种模型(基准模型)是基于不完全密封约束下得到的,即借款人和贷款人的报价是密封的信急,而贷款配额是所有贷款人共同知道的信急.第二种模型(拓展模型)是基于完全密封约束下得到的,即借款人和贷款人的报价、配额都是密封的信急.通过算例分析也表明,双边密封拍卖机制的支付水平随着激励系数(或惩罚系数)的变化而变化.特别地,在激励系数(或惩罚系数)不断增大的过程中,贷款人的拍卖策略会不断向下扭曲,使得贷款人无法实现收益最大化.因此,双边密封拍卖可以从一定程度上制约贷款人的决策,有利于降低借款人的支付成本.
最后指出,相关理论设计与分析是在有效监管背景下进行的,没有充分考虑贷款人的逆向选择、道德风险等问题,在实际应用中可能存在一定的局限性,后续将进一步放宽假设.同时考虑到这类拍卖机制在实际中尚未得到应用,无法收集相关数据进行实证分析,后续将进行实验,分析贷款人和借款人的投标策略、借款紧迫性等变量对该拍卖机制的影响.

