随机需求条件下的P2P网络借贷拍卖机制
周正龙,马本江,胡凤英
(1.华中师范大学信息管理学院,湖北 武汉 430079; 2.中南大学商学院,湖南 长沙 410083)
1 引言
拍卖在日常生活中已普遍存在,并且已经深入到市场各个领域,包括供应链采购[1]、资源分配[2]、网上电子商务交易[3]等。近几年来,拍卖机制也被拓展到P2P网络借贷市场,用以分析贷款人(即资金的提供者)和借款人(即资金的需求者)之间的利益关系。例如,Chen Ning等[4]对Prosper平台的交易机制进行了详细的研究,并给出了Prosper拍卖的一般模型。从实际情况来,目前一些P2P网络借贷平台是重点关注拍卖交易的典型平台。例如,英国的Funding Circle、德国的 Innovestment等平台的主要交易模式是贷款人之间自行竞拍,通过贷款人拍卖确定借贷利率(更多关注贷款人的行为)。然而,目前国内有关P2P网络借贷市场的研究主要侧重于风险控制[5]、行为决策[6]、信任与监管[7]等方面,较少文献从拍卖的角度去探讨中国P2P网络借贷的交易机制问题。因此,有必要从拍卖的角度,分析中国P2P网络借贷交易机制存在的不足,并用拍卖理论改进目前的交易机制。
目前,针对中国P2P网络借贷市场的拍卖研究尚不多见,但可以通过一些相关文献观察到拍卖机制在解决融资、定价等问题方面的重要性。例如,邱甲贤等[8]研究了Prosper平台在使用拍卖机制期间的定价策略问题,并指出贷款人和借款人之间存在显著的正交叉网络外部性和自网络外部性,交易价格弹性随平台定价策略的变化而变化。随后,段文奇、柯玲芬[9]以及刘维奇等[10]进一步考察了平台竞争的变化对动态定价策略效果的影响,并指出合理的机制设计在动态定价中的重要性。在融资问题上,中国P2P网络借贷拍卖机制类似于网上临时一口价拍卖,考虑了投标者在交易过程中的有限理性行为[11],在一定程度上可以有效规避投标者的羊群行为。同时,P2P网络借贷市场通过网络拍卖进行交易,同样可以实现最优借款策略和贷款人的均衡投标策略[12]。进一步地,周正龙等[13]也论证了竞标方式比文字描述能更好地解决P2P借贷融资、定价等问题,竞标方式可以更好地披露借款人信息,激励借款人在还款过程中履行借款约定,有良好信誉记录的借款人能够获得更低成本的借款。因此,在解决P2P网络借贷市场的融资、定价等问题上,可以通过拍卖理论设计适合于P2P市场的交易机制,这不仅是对了解和规范该类平台发展提供相关的理论依据,也是对第三方交易市场理论研究的一种补充。
在此背景下,本文以P2P网络借贷市场为对象,借鉴Duenyas等[14]的简单拍卖机制,设计了一种两阶段的P2P网络借贷拍卖,用以改进和完善中国P2P网络借贷市场的交易机制。相比Chen Ning等[4]研究的Prosper拍卖机制,这个两阶段P2P借贷拍卖最主要的特征是,贷款人比较容易接受这个拍卖机制,并且有利于降低借款人的支付成本。这个机制的第1阶段是标准降价拍卖的简单拓展,类似于Wu等研究的Multi-winner 拍卖[15];第2阶段在其他很多领域中是很常见的。例如,在供应链采购合同拍卖中,通常用两种类型机制来筛选供应商:一个是竞争性报价,即每个供应商提交一个支付报价,然后公司选择一个中标人;另一个是合同谈判,即公司通过一个执行菜单让这些供应商去选择他们偏好的属性。此外,黄河等[16]设计了两阶段采购机制,该机制先实施关于合同的拍卖,再执行可能的议价谈判。因此,本文设计的阶段2就类似于黄河等研究的议价谈判,其差异性主要在于本文的阶段2是在借款人需求实现之前完成的,并且这个机制让借款人把握了借款需求的控制权,也意味着借款人在实际过程中更容易采取这种机制。
进一步地,相比Duenyas等[14]设计的简单拍卖机制,这个两阶段P2P借贷拍卖最主要的特征是,所有贷款人参与了一种的关闭式拍卖,即贷款人提交并更新报价,直到借款需求满足时关闭拍卖。这个机制的阶段1会产生多个中标人,随后进一步参与阶段2的竞争,并产生阶段2的唯一中标人;而Duenyas等[14]设计的阶段1只产生一个中标人,而且阶段2的中标人不变。但是与Duenyas等[14]设计的机制一致,本文设计的机制在没有影响最优结果的情况下,通过两阶段信息的筛选过程实现了关闭式拍卖的简单性,而且在筛选的过程中可以不断缩小借款人的支付成本。事实上,支付成本的缩小主要是来自于贷款人之间的竞争关系,并且这个竞争关系是基于借款人设计的拍卖机制实现的。这类似于汪定伟[17]提出的捆绑与组合结合的两轮逆向拍卖机制,在符合资质要求的贷款人数量不确定的情形下,通过最优的捆绑方案激化贷款人在竞标过程中的竞争关系,从而使得借款人获得更好的经济效益。
2 基准模型:对称贷款人
本文考虑一个类似拍拍贷撮合机制的网络借贷问题,1个借款人对n个候选的贷款人,并且贷款人拥有关于报价的私人信息。在借款人使用借款进行项目融资之前,为了满足他的最佳借款需求,借款人需要从1个或n个贷款人那里获得借款,并且借款期限设置为1年以内(即不考虑复利的影响)。因为每个贷款人的报价是他们的私人信息,交易的合同利率或价格就变得不固定,需要通过与贷款人的交流来确定。所以,借款人需要设计一个交易机制来确定最终的借款需求和合同利率(合同利率或价格等价于借贷双方最终确定的借款利率,均设定为年利率),以及从哪些贷款人那里获得需求。这里先给出以下两个背景假设:(1)假设在整个拍卖的过程中不存在借款人和贷款人的套利行为、P2P平台商之间的暗箱操作。 (2)假设P2P网络借贷平台能有效控制借贷风险,并且不存在P2P庞氏骗局现象。需要指出的是,P2P网络借贷市场上的套利交易类似于货币市场和期货市场上的套利交易,可以理解为借款人或贷款人从一家P2P平台借入资金后转向另一家P2P平台借出该资金,以期在差价中获得利息差的经济行为。P2P网络借贷市场上的暗箱操作是指利用职权暗地里做一些不公正、不合法的事情,可以理解为平台商或平台经理人团队利用职权在后台协助借款人获得资金的行为。
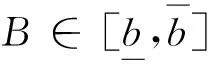
(1)
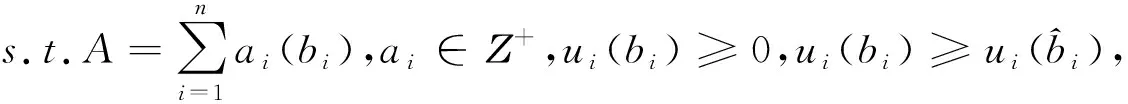

(2)
定义虚拟竞价函数ψ(b)=b+F(b)/F′(b),并且容易得到,所有贷款人Li都满足ψ(b)关于b是递增的(这里也体现了对称贷款人的特征,即所有贷款人的虚拟竞价函数是一样的)。这是一个常规性的条件,经常在拍卖环境中被假设出来(见Myerson[20]),并且F(b)/F′(b)关于b是递增的假设等价于F(b)是对数凹的[21]。于是,机制设计问题变为:
(3)

定理1:根据下标(i)指出虚拟竞价函数顺序ψ(b1)≤…≤ψ(bn),可得到需求规则以最低虚拟竞价来确定一揽子借款是最优的,并满足A*(b)=max{A∈Ζ|r(A)≥ψ(b)},b=min{bi|bi≤bj≠i, ∀j∈[1,n]}。
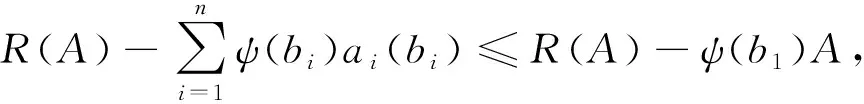

接下来,结合借贷契约和借款需求规则,就可以获得借款人的拍卖机制,具体如定义2所示:
定义2:对于任意的P2P网络借贷拍卖机制,如果满足如下两个阶段性条件,就可以称为两阶段的关闭式降价拍卖(Open-descending Closed Auctions with Two Stages,简称TS-OCA机制)。其中,阶段1是对初始借款需求A0的借贷契约进行一次关闭式降价拍卖;阶段2中,借款人可能会通知所有中标的贷款人,想从他们那里获得额外的借款需求(这个需求是在A0以上的额外数量)。
相应的拍卖规则如下:在阶段1中,借款人宣布进行一次关闭式降价拍卖,并且拍卖价格p以一个较高的价格被借款人提出来;随后,任意的贷款人Li在规定时间内提供(并更新)报价和配额参与拍卖;如此进行累加,直到最后一个成功贷款人提供的配额与已有配额加总的供给量大于等于初始借款需求A0时关闭拍卖(这里的A0可以根据定理1演化得到),并将所有中标人的报价从小到大进行排序,以最后一个成功贷款人的报价为所有中标人的合同利率;否则,直到截止时间宣布拍卖结束。假设拍卖在价格为p0处结束,那么所有中标人有义务交付各自的配额,加总构成A0单位资金给借款人,借款人也将支付给所有中标贷款人相应的报酬,并且A0单位资金的借款利率为价格p0。在阶段2中,借款人可能会通知所有中标的贷款人,他需要一笔额外的借款需求,并宣布最先提供额外需求的贷款人为阶段2的唯一中标人。这个通知指出,每个额外需求的单位价格直到拍卖结束之后才被公布,每个额外借款需求的单位价格不高于拍卖价格p0。所有中标贷款人可以自愿交付任意的额外数量。宣布这个规则之后,借款人可以按如下过程执行这个拍卖机制:

(1)确定初始借款需求A0=max{A∈Z|r(A)≥ψ(b)},并且满足r(1)≥ψ(b)以实现A0≥1;(2)单位借款需求的关闭式降价拍卖以价格b开始;(3)重复(2)步骤,直到阶段1的降价拍卖结束,比如阶段1的拍卖以价格p0结束,且贷款人L1,…,Lk是中标人;(4)确定阶段1的所有中标人后,借款人发出通知以确定阶段2的唯一中标人 ,并且为第 k个额外单位提供的支付为min{p0,ψ-1(r(a+A0))},第k个额外单位的资金是贷款人Li自愿交付的,满足k≤r-1(ψ(b))-A0;(5)输出总的借款需求和相应的支付价格序列。
简而言之,TS-OCA机制采用以下拍卖模式:借款人用一个关闭式降价拍卖去分配一个初始借款需求的合同。在拍卖之后,借款人向所有中标贷款人发出一个额外的通知,想以更低价(打折价)获得更多的借款需求。值得注意的是,两个阶段都是发生在借款人需求实现之前的,因此不影响总借款需求的最优性,对借款人而言是占优的。这里首先指出,在阶段1中所有中标贷款人的真实报价和配额构成一个纳什均衡,具体如引理1所示:
引理1:在TS-OCA机制的阶段1中,所有中标贷款人的真实报价和配额构成一个纳什均衡,这也说明贷款人的占优策略是报告自己的真实类型。
证明:根据TS-OCA机制执行过程中的(2)和(3)可知,当任意Li参与竞标并成为中标人时,贷款人Li单方面增加报价bi就演变为当前报价序列B=(b1,…,bk)中最后一个成功的贷款人,这里将Lk定义为B中最后一个成功的贷款人。这说明在重复增加报价后没有贷款人可以获得更多的效用,这时贷款人Lk在中标人集合中的报价不可能高于bk,否则他的配额将为0。所以按照TS-OCA机制执行过程可知,贷款人Lk从真实利率的序列开始执行,并且仅仅中标人集合中的贷款人能增加报价,所以中标人集合中所有的贷款人均能成功进行贷款,且满足Lk在中标人集合中保持不变。进一步地,贷款人Lk是最后一个增加报价的贷款人。因此,贷款人Lk不可能通过降低报价获得更多的效用,这时的报价序列B=(b1,…,bk)就是一个纳什均衡。进一步地,在TS-OCA机制单次交易模型中,只要最后一个成功贷款人Lk的投标是有利可图的,那么每个成功贷款人都会趋向于耗尽自己的预算配额,并且耗尽预算配额是整个分配问题的唯一最优解,使用反证法不难得到。这也说明了,所有成功贷款人的占优策略是耗尽自己的预算配额,即报告自己的真实配额[13]。证毕。
引理1说明,在TS-OCA机制中,贷款人有动机报告自己的真实类型,因此借款人按照阶段1的执行过程就可以获得所有中标贷款人都能接受的最低利率p0,进一步结合阶段2就可以构成借款人的一个最优机制,具体如定理2所示:
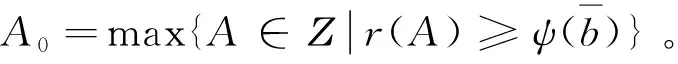
证明:首先来说明一个关闭式的竞拍过程,并且p≥bi是贷款人Li的占优策略(这里的bi表示贷款人Li的私人真实利率,具体分析见引理1):当p≥bi时,如果拍卖结束且贷款人L1,…,Lk是阶段1的中标人,那么他们交付的总额仅仅能达到规定的A0单位,保证一个非负的收益p≥bi。另一方面,如果他们错过这个拍卖,那么贷款人L1,…,Lk的收益都为0。因此,所有成功参与竞拍的贷款人L1,…,Lk将不断降低竞拍报价,直到最后一个成功的贷款人获得最后一个配额。当p sup{b|ψ(b)≤ψ(bi),∀i≥k+1,ψ(b)≤r(a+A0)}=max{b|ψ(b)≤ψ(bi),∀i≥k+1,ψ(b)≤r(a+A0)}。这表示阶段2为任意中标贷款人Li提供了一个阈值,如果阶段1中最后一个成贷款人Lk的报价bk低于这个阈值ψ-1(min{ψ(bk+1),r(a+A0)}),那么借款人将从任意中标贷款人L1,…,Lk那里获得第k个额外单位的资金。因此,贷款人Li的总配额为xi=max{ai∈Ζ|bk≤max{b|ψ(b)≤ψ(bi),∀i≥k+1,ψ(b)≤r(ai)};同时对阶段2中任意中标人Li而言,愿意交付给借款人额外需求量为a0=max{a∈Ζ|r(a+A0)>ψ(bi)}。因此,TS-OCA机制对于借款人而言是一个最优机制。证毕。 这个机制对于贷款人而言是熟悉的,阶段1仅仅是关于初始借款需求的关闭式降价拍卖。在拍卖后,借款人可能会提供一个额外的条件给所有中标的贷款人,这样的结果对于贷款人而言也是最优的,因为这个可能的额外通知不会影响贷款人在阶段1中的拍卖策略,而且最后一个成功的贷款人Li将坦白地降低拍卖价格,直到这个价格接近贷款人的私人真实利率bi,同时借款人也没有动机去提供一个高于阶段1的拍卖价格。事实上,借款人和贷款人都已经理解,如果贷款人能进一步降低价格,那么借款人可能会借款更多。为了确定这个最佳的额外借款量,贷款人仅仅只需要再次比较他的真实私人利率与不断递减的支付序列之间的大小,以找出最后一个能获利的分配量,然后就可以交付这个额外的数量。 定义3:对于任意的P2P网络借贷拍卖机制,如果满足如下两个阶段性条件,就可以称为修正偏见的两阶段关闭式降价拍卖(Modified Biased Open-descending Closed Auction with Two Stages,简称TS-MOCA机制)。其中,阶段1对提供A0单位的借款契约而言是一个修正偏见的关闭式降价拍卖;阶段2中,借款人可能会通知所有中标的贷款人,他想从他们那里获得额外的借款需求。 (1)确定初始借款需求A0=max{A∈Z|r(A)≥ψ(bi), ∀i},并且满足r(1)≥ψ(bi)以实现A0≥1;(2)买方首先告知每个贷款人Li关于他的偏置函数H(·);ψi(·)(3)A0单位合同的降价拍卖以单位价格min{ψi(bi)}开始;(4)重复(3)步骤,直到阶段1的降价拍卖结束。比如阶段1的拍卖以价格p0结束,且贷款人L1,…,Ln是中标人;(5)确定阶段1的所有中标人后,借款人发出通知以确定阶段2的唯一中标人Li,并且为第k个额外单位需求提供的支付为ψ-1i(minp0,(r(a+A0))}),第a个额外需求是贷款人i选择交付的,满足a≤max{l|r(l+A0)>ψi(bi)};(6)输出总的借款需求和相应的支付价格序列。 相比TS-OCA机制,TS-MOCA机制主要的特征是阶段1加入了偏置函数,以修正拍卖机制对较高Bi贷款人的偏见。在阶段1拍卖之后,借款人同样向所有中标的贷款人发出一个额外的通知,他想以更低价(打折价)获得更多的借款需求。对此,也可以进一步给出如下的定理: 下面按照本文对初始借款需求的计算公式就可以计算出这个机制的初始需求量: (4) 这样就可以得到A0=88.5。于是阶段1中的关闭式降价拍卖可以描述如下:“请按照关闭式降价拍卖规则,为88.5单位的借款需求提供一个报价和配额”。假设拍卖的最终定价(即借款利率)是0.15(15%),并且L1,…,L10的配额集合A={a1,…,a10}为{20,18,14,10,8,7,6,3,1.5,1},那么借款人为第k个额外单位的借款需求支付的额外价格满足min{p0,ψ-1(r(a+A0))}。为了得到这个结果,本文算出: (5) 所以,min{p0,ψ-1(r(a+A0))}=min{0.15,(12.5-a)/20}。这个额外的通知将单独给阶段2的中标贷款人:“除了您承诺在阶段1交付的借款数额之外,我愿意再借款11个额外单位的数量,并且在您选择交付的情况下,我对第1个至第9个额外单元数量的支付价格是0.15(15%)、对第10个的支付价格是0.125(12.5%)、对第11个的支付价格是0.075(7.5%)”。很明显,对于后进入拍卖的贷款人尤其是最后一个成功的贷款人而言,上述的实施的阶段2对他的诱惑性更大,因为他在阶段1中所交付的配额不多,获利不大,所以在阶段2会趋向于跟进拍卖,以期扩大自己的总收益。 进一步假设贷款人L10成为阶段2的唯一中标人,于是结合定理2可以得到,借款人给贷款人L10的最优支付为: (6) 借款人给其他中标贷款人Lj≠10的最优支付为 vj≠10=aj≠10p0={3,2.7,2.1,1.5,1.2,1.05,0.9,0.45,0.225} (7) 此时,如果设定借款单位为百元,就可以得到该机制的分配结果,具体如表1所示: 表1 TS-OCA机制下的分配结果 此时,如果所有贷款人按照拍拍贷平台的撮合机制进行竞拍,并且按照年利率15%计算,拍拍贷平台给所有贷款人的最优支付为 (8) 同样地,设定借款单位为百元,就可以得到拍拍贷机制的分配结果,具体如表2所示: 表2 拍拍贷机制下的分配结果 结合表1和2的结果得到,在不影响机制最优性的情形下,采取本文设计的机制有利于降低借款人的成本。所以,借款人选择本文设计的机制是占优的。 接下来分析贷款人的占优策略。如果所有贷款人将资本存入银行(简称银行机制),并且按照定期存款(五年)的年化利率2.75%计算,银行给所有贷款人的最优支付为: (9) 同样地,设定存款单位为百元,就可以得到银行机制的分配结果,具体如表3所示: 表3 银行机制下的分配结果 结合表1至3的结果得到,贷款人把闲余资金放到P2P平台比放到银行要划算些,但是不同行业之间的风险程度也不同,不能做直接的判断。只能从拍卖机制的角度得出,如果借款人与贷款人之间实现借贷合同,并得到有效保障的前提下,贷款人把闲余资金放到P2P平台是占优的。进一步地,如果借款人选择本文设计的拍卖机制,贷款人也有动机参与竞标。所以,在实际运行过程中,只要能实施有效的监控机制保证P2P网络借贷交易机制的正常运行,那么本文设计的拍卖机制可以进一步降低借款人的成本,同时使得贷款人也容易接受这种机制。这相对于目前中国类似拍拍贷等提供的撮合机制也是一个有效的改进方案,特别是在不影响机制最优性的情形下,进一步降低了借款人的成本。因此,本文设计的两阶段关闭式降价拍卖可以用于改进和完善中国P2P网络借贷平台的交易机制。 在P2P网络借贷契约设计中,本文提供了一种关于随机借款需求的两阶段关闭式降价拍卖,并构成了借款人的一个最优机制。这个机制主要由两个阶段组成(都发生在借款人需求实现之前)。阶段1中,首先确定初始借款需求,随后进行一次关闭式降价拍卖;阶段2中,借款人给出的一个附加通知,以获得一个额外的借款需求,并且额外需求的价格不高于阶段1所支付的价格。进一步地,在本文设计的机制中,借款人是基于竞价函数去比较贷款人,而不是基于虚拟成本;同时,在给定的基准模型中,阶段1的降价拍卖不能被任意其他拍卖版式替代,以揭露贷款人的私人真实利率。特别地,在不影响机制最优性的前提下,阶段1的降价拍卖不能被一级价格密封拍卖、二级价格密封拍卖以及升价拍卖替代。最后,通过数值算例指出,这个机制相对于目前中国类似拍拍贷等提供的撮合机制是一个有效的改进方案。 综上,针对中国目前P2P网络借贷机制的不足,可以将两阶段的关闭式降价拍卖作为一种改进或补充机制,同时在达成交易之后生成借贷契约或合同,使得借款人和贷款人之间实现纸质合同交易,在一定程度上既可以提高借贷关系的法律效力,又可以有效降低违约风险,进而提高拍卖机制对中国P2P行业的市场效率,这也有利于中国P2P网络借贷市场的健康发展。最后指出,在整个本文研究的过程中,主要立足于交易机制的设计与分析,没有考虑借款人和贷款人的套利行为、P2P平台商之间的暗箱操作等问题,所以本文的下一步研究方向是进一步缩短假设条件,用以论证和改进本文设计的拍卖机制,进而对中国P2P行业的健康发展做出贡献。 参考文献: [1] Chen Fangruo. Auctioning supply contracts [J]. Management Science, 2007, 53(10): 1562-1576. [2] Zhang Yang, Lee C, Niyato D, et al. Auction approaches for resource allocation in wireless systems: A survey [J]. IEEE Communications Surveys & Tutorials, 2013, 15(3): 1020-1041. [3] Zhang Hong, Jiang Hongbo, Li Bo, et al. A framework for truthful online auctions in cloud computing with heterogeneous user demands [J]. IEEE Transactions on Computers, 2016, 65(3): 805-818. [4] Chen Ning, Ghosh A, Lambert N S. Auctions for social lending: A theoretical analysis [J]. Games and Economic Behavior, 2014,86: 367-391. [5] Wei Shen. Internet lending in China: Status quo, potential risks and regulatory options [J]. Computer Law & Security Review, 2015, 31(6): 793-809. [6] Liu De, Brass D J, Lu Yong, et al. Friendships in online P2P lending: Pipes, prisms, and relational herding [J]. MIS Quarterly, 2015, 39(3): 729-742. [7] Chen Dongyu, Lai Fujun, Lin Zhangxi. A trust model for online peer-to-peer lending: A lender’s perspective[J]. Information Technology and Management, 2014, 15(4): 239-254. [8] 邱甲贤, 林漳希, 童牧. 第三方电子交易平台运营初期的定价策略——基于在线个人借贷市场的实证研究[J]. 中国管理科学, 2014, 22(9): 57-65. [9] 段文奇,柯玲芬. 基于用户规模的双边平台适应性动态定价策略研究[J]. 中国管理科学, 2016, 24(8): 79-87. [10] 刘维奇, 张苏. 双边平台兼并策略下的定价问题分析[J]. 中国管理科学, 2017, 25(5): 17-24. [11] 高广鑫, 樊治平. 考虑投标者有限理性行为的网上临时一口价拍卖的卖方收益分析[J]. 中国管理科学, 2017, 25(7): 102-112. [12] 刘树人, 唐沛, 黄颖娜. 网上拍卖销售与逆向拍卖采购下的库存管理[J]. 中国管理科学, 2015, 23(11): 62-69. [13] 周正龙, 马本江, 胡凤英. 中国P2P网络借贷平台的动态逆向拍卖机制[J]. 系统工程理论与实践, 2017, 37(2): 409-417. [14] Duenyas I, Hu Bin, Beil D R. Simple auctions for supply contracts [J]. Management Science, 2013, 59(10): 2332-2342. [15] Wu Yongle, Wang Beibei, Liu K J R, et al. A scalable collusion-resistant multi-winner cognitive spectrum auction game[J]. IEEE Transactions on Communications, 2009, 57(12): 3805-3816. [16] 黄河, 陈剑. 拍卖采购合同及议价谈判机制设计[J]. 管理科学学报, 2010, 13(3): 1-7. [17] 汪定伟. 网上集中采购的捆绑-组合拍卖机制设计[J]. 系统工程学报, 2011, 26(6): 809-816. [18] 马本江, 姜云芳, 陈晓红. 存在应收账款条件下中小企业不足额质押融资合同设计[J]. 中国管理科学, 2015, 23(12): 35-44. [19] Krishna V. Auction theory [M]. Massachusetts: Academic Press, 2009. [20] Myerson R B. Optimal auction design [J]. Mathematics of Operations Research, 1981, 6(1): 58-73. [21] Rosling K. Inventory cost rate functions with nonlinear shortage costs [J]. Operations Research, 2002, 50(6): 1007-1017. [22] Rezende L. Biased procurement auctions [J]. Economic Theory, 2009, 38(1): 169-185. [23] Vickrey W. Counterspeculation, auctions, and competitive sealed tenders [J]. The Journal of finance, 1961, 16(1): 8-37.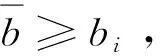
3 拓展模型:非对称贷款人
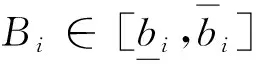
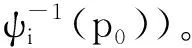

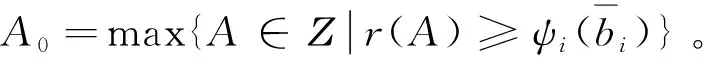
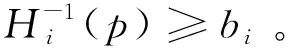
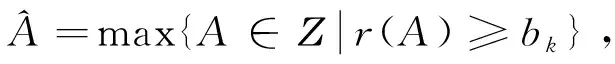
4 算例分析与比较
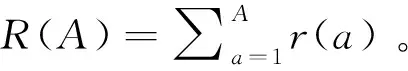
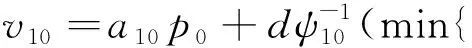



5 结语

