基于AR(1)需求模式和固定间隔期订货点法的牛鞭效应分析
周章金,郭进利
(上海理工大学,上海 200093)
0 引言
1961年Forrester首先发现需求随着供应链上游逐级放大的现象并做了相应的研究,初步揭示了供应链中时间延迟、需求放大等动态性的存在,该现象被称为“牛鞭效应”,同时也被称为“Forrester效应”。目前对这种现象的称谓很多,有一般人所熟知的“蝴蝶效应”,也有称为牛鞭效应、长鞭效应、供应链需求信息的扭曲、信息时滞。
1984年,麻省理工学院的J.D.Sterman教授为证实牛鞭效应的存在主持了一项供应链物流管理动态模拟实验——啤酒实验。实验结果显示:每个经营者都有自己的库存量决策依据,他们相信市场波动是外部因素造成的,而消费者需求正是顺应这种波动而发生变化的。
美国斯坦福大学的教授Lee及其合作者把导致牛鞭效应的原因归纳为以下5种原因:(1)需求信号处理;(2)限量供应和短缺博弈;(3)交货时间延迟;(4)价格波动;(5)批量订货[1]。
本文研究牛鞭效应与其他的定量研究有所不同,本文不考虑供应链中的预测因素,而只考虑非预测因素对牛鞭效应的影响。通过基于AR(1)的需求模式和订货点法的库存策略,分析了平滑期、相关系数及提前期等对牛鞭效应的影响,并为尽可能减少牛鞭效应提出了一些方法手段。
1 模型假设及前提
本节的研究对象是由1个零售商和1个生产商组成的简单两级供应链系统。假设零售商是生产商的唯一买方,他们之间只交易1种产品。双方的行为发生在一个无限离散的时间范围内,即 t=-∞,…,-1,0,1,…,∞。 零售商从发出订单到收到货物的时间(即提前期)L[2][3]。
用于模拟终端顾客的需求的方法有从简单的独立同分布到动态非稳定的一系列随即过程。实践证明,没有任何一种需求预测的方法能够完全真实的反映实际的情况。由于AR(1)模拟终端顾客需求较为成熟,且计算难度不大,成为众多学者优先选择的对象。
同时零售商可采用的需求预测的方法也是琳琅满目,例如,一次移动平均法SMA、二次移动平均法DMA、一次指数平滑法SES、布朗单参数指数平滑法BSES、霍尔特双参数指数平滑法HDES、温特季节性指数平滑法WSES等等。本文仅采用一次移动平均法SMA。
因此,我们假设零售商面对的终端顾客的需求为一个简单的平稳AR(1)自相关时间序列:

式中:Dt:t时期终端顾客的需求;
μ:非负常数;
ρ:相邻两个时期终端顾客需求之间的相关系数,|ρ|<1为需求平稳的条件;
εt:市场需求的变动误差,且εt为满足均值为0,方差为σ2的独立同分布随机变量。
由(1)式我们很容易导出Dt的均值及方差:


图1 需求预测过程中的牛鞭效应(-1<ρ<1,P=5;P=8)
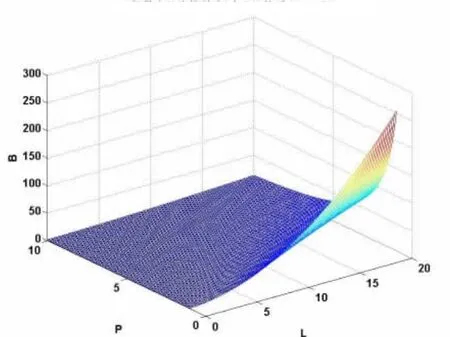
图2 二级供应链牛鞭效应L与P的关系(ρ=0.7)
在这里,我们可以注意到,变量取不同的值代表了不同的需求模式:当μ=0,ρ=1时,需求为随即游走过程;当ρ=0时,需求为均值为μ,方差为σ2的独立同分布过程;当-1<ρ<0时,相邻两期需求负相关,过程呈现振荡行为;当0<ρ<1时,相邻两期需求正相关,过程呈现波动趋势;当|ρ|→1时,需求过程呈非稳定状态[4]。
2 需求预测过程中的牛鞭效应
移动平均法简单易用,且效果不错,被广泛应用于企业的经营管理中。假设零售商采用移动平均法,平滑期为p,则零售商对时期t的需求预测为:

式中:Dt-i:终端顾客在t-i时期的实际需求。
考虑到订货提前期L,这段时期内的总需求预测为:

由(3)式我们可以得出:
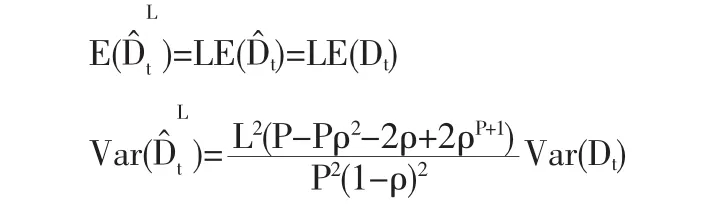


由图1我们可以看出固定ρ,增加平滑期P能够减小牛鞭效应,但随着P增加减小作用减少;提前期L越长,牛鞭效应越显著,同时L小于某最小值时,没有牛鞭效应发生,该最小值随着ρ的增大而减小。
3 信息处理过程中的牛鞭效应
零售商对终端顾客的需求做出预测后,需要根据自己的库存策略向生产商进行订购。在经典的库存理论中,有固定量系统,固定间隔期系统和最大最小系统。公司一般都是间隔一定时期来在ERP系统中Run MRP,故采用与Run MRP相同周期的固定间隔补货期是经济合理的。即每隔一个周期,采用订货点法将库存补充到一个最高水位yt。有[5]:

yt:零售商采用订货点法的得到的t期的最高库存;

那么零售商向生产商发出订单的数量为:

将(3)(7)带入(8),有:

为了方便起见,我们令z=0,故上式有:

则qt的方差为:
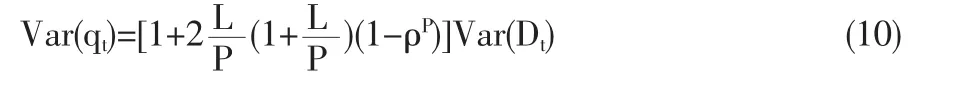
令B表示信息处理过程中的牛鞭效应,有:

由于前面有假设|ρ|<1,故(1-ρP)>0,因此 B>1,即零售商向供应商发出的订货量始终大于终端顾客的实际需求Dt。进一步分析,有:



因此,随着提前期L的增大,牛鞭效应将增大;平滑期P越长,牛鞭效应将减小。
至于 ρ,应该分类讨论,当 0<ρ<1 时,∂B/∂L<0,即相关系数ρ越大,牛鞭效应越小;当ρ=0时,B=1+2L/P(1+2L/P),牛鞭效应ρ与值无关,仅取决与L/P的比值;
当-1<ρ<0 时,若 P 为偶数,∂B/∂L>0,即相关系数 ρ越大,牛鞭效应越大;
若 P 为奇数,∂B/∂L<0,即相关系数 ρ 越大,牛鞭效应越小。
4 信息传递过程中的牛鞭效应
本文研究的是耳机供应链系统,如果生产商与零售商之间没有进行信息共享,那么生产商在向上一级订购原材时,也只能根据零售商以前向他订货的历史数据来进行预测,即零售商的订购模式就是生产商的需求模式。
将(1)式带入(9)式得生产商在t时期对零售商的需求预测为:

进一步推导qt的均值和方差:
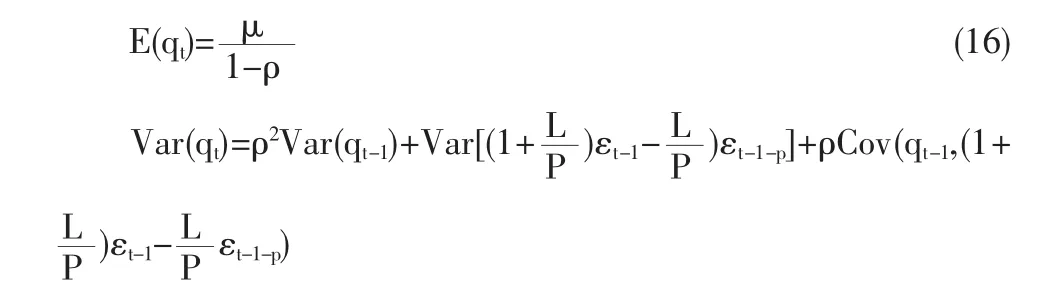
移相整理得:

我们可以观察到(17)式中的牛鞭效应的表达式与(11)一样。同时由(15)我们可以观察到,当终端顾客的需求信息为AR(1)的时间序列时,零售商采用移动平均法的预测方法和订货点法的库存策略时,生产商与零售商之间信息不共享,那么生产商的需求预测为一个ARMA(1,P)的随机过程。
5 小结
本文推导了基于AR(1)需求模式和订货点法的二级供应链牛鞭效应的量化模型,推导了零售商在对终端顾客的需求预测中,零售商在向生产商订货的信息处理过程中,生产商在预测零售商的订货数量的信息传递中的牛鞭效应,并得出了相关结论。为定量计算牛鞭效应提供了依据,也为进一步研究供应链系统提供了基础。
[1]Lee H L,Padmanabhan V,Whang S.The Bullwhip Effect in Supply Chains[J].Sloan Management Review,1997,23.
[2]刘红,王平.基于不同预测技术的供应链牛鞭效应分析[J].系统工程理论与实践,2007,(7).
[3]曹庆仁,周敏,宋学锋.固定间隔期补充定货策略中牛鞭效应的计算[J].中国矿业大学学报,2004,(5).
[4]万杰,寇纪淞,李敏强.需求信息预测与处理中的牛鞭效应[J].天津大学学报,2003,(5).
[5]刘红.供应链牛鞭效应研究[D].上海海事大学,2006.

