带趋势的二元选择面板数据模型估计
韩本三
(西南财经大学 统计学院,成都 610074)
0 引言
微观面板模型是个有趣的也是富有挑战性的研究领域。因为面板数据模型由传统的线性过度到非线性面临很多问题而且不同的数据类型处理方法上也差别很大。最基本的模型是带有固定效应的二元面板模型,称为两时期两状态模型(见Arellano和 Honore,2001)。这个二元模型是个潜变量模型,因变量被描述为解释变量的线性组合与个体固定效应以及随个体时间而变化的设定冲击的和。我们感兴趣的参数是解释变量的系数。如果我们用通常的极大似然法估计,会产生“意外参数问题(Baltige,2005)。因为随着个体数N增加固定效应的个数也在增加。对于Logit模型,Chamberlain(1980)发现二元因变量按时间求和对个体固定效应是个最小的充分统计量(即 S-充分性,Barndorff-Nilsen,1987)。这样便得到了解释变量系数的条件Logit估计。这种方法的一个关键假设是设定冲击间相互独立性。Magnac(2004)在没有冲击独立的条件下,推广了条件Logit模型,提出了相应的半参数估计。
1 冲击独立下的条件Logit估计
基本模型如下:
yt=1,当且仅当 xtβ+ηt+ε+μt>0;否则 yt=0
其中t=1,2,3,4;xt是L维实向量。为简便模型省略了个体下标 i。
假设R:
(1)x1(1)-x2(1)-x3(1)+x4(1)在整个实线上连续变化,xt(1)表示 xt的第一个分量,β(1)=1,即β的第一个分量为1;
(2)x1-x2-x3+x4的取值不共线;
(3)随机冲击(μ1,μ2,μ3,μ4)具有严格正的、连续的、有界的密度函数,并且与x1,x2,x3,x4,η,ε独立。
假设(1)和(2)是为了保证模型能够被识别,参照Magnac(2004)。假设(3)是为了得到充分统计量的一个等价刻画。对于条件 Logit估计,μ1,μ2,μ3,μ4还被假设为独立的, 并且服从Logistic分布。

当K=0或4时,上述结论显然是成立的。下面说明当K=1时结论是成立的,其他情况类似。当K=1时会有四种情况出现,我们选择y1=1,y2=y3=y4=0来说明

证明:容易知道K和S的取值范围分别为{0,1,…,3,4}和{0,1,…,8,10}。当K=0,4或S=0,10时,结论显然成立。因为K,S取值是相关的,根据其范围我们可得只有当K=2,S=5时,y1,y2,y3,y4的取法才不唯一,此时y1=1,y2=y3=0,y4=1或y1=0,y2=y3=1,y4=0。
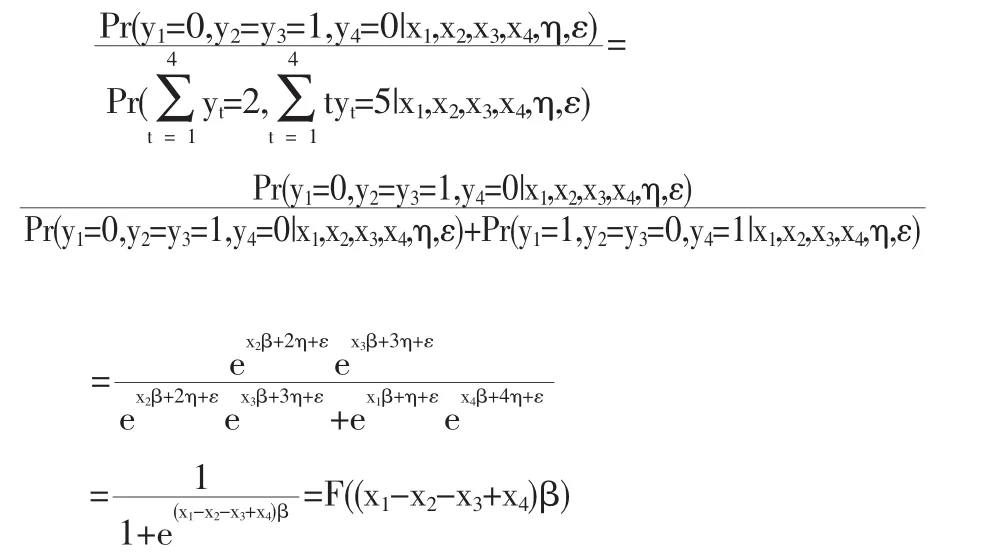
上述结果与η和ε无关。同理可得

从而我们可以写出条件似然函数为

其中当 y1=0,y2=y3=1,y4=0时,wi=1;当y1=1,y2=y3=0,y4=1时,
对于T>4的情况,我们可以对个体时间序列按相邻的四个作为一组,构造似然函数,可以证明似然函数形式是相同的,区别仅在于K和S的取值上。这种方法虽然在一致性上没有问题,但对于有效性,还有值得考虑的地方,因为我们将一个四期的面板模型转化为了一个截面数据模型。
2 充分性的等价刻画
第二部分的条件Logit估计方法有两个很强的假设:μt间的相互独立性和Logistic分布假设,因而受到批评(Magnac,2004)。 正如 Magnac(2004)中的做法,我们希望能够在没有冲击独立的假设下得到其似然函数,对于Logistic分布假设,一个自然的方法是利用半参数方法。充分性定义仍然和前面一样:
下面我们给出充分性的一个等价刻画。
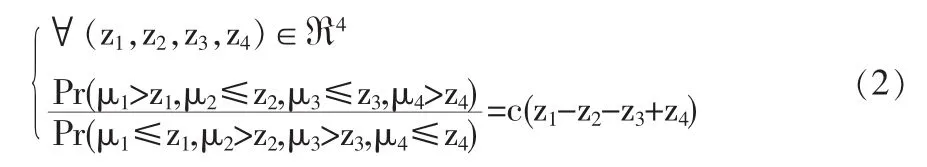
证明:令 zt=-xtβ-ηt-ε,根据假设 R(3)有

由充分性定义,我们只需要证明对(y1,y2,y3,y4)∈{(1,0,0,1),(0,1,10)}定理1成立。因为在对条件下,其概率和为1,所以我们只需要考虑一种情况就可以了。

根据假设 R 可知 r(z1,z2,z3,z4)在 R4是光滑的,并且 z1,z2,z3,z4在整个实轴上变动。
这样要使得 r(z1,z2,z3,z4)与 η、ε 无关,即有 z1,z2,z3,z4一种组合能够消除η和ε,并且能够保留我们需要估计的参数β。 因为 xt可能导致线性无关性,我们只需要考虑 z1,z2,z3,z4的线性组合。这样只存在两类组合方式:z1-z2-z3+z4和(z1-z4)+3(z3-z2)。其他组合是这两种组合中一种的常数倍,所以我们只需要考虑这两种类型。假设

在假设 R 下,当 z1→∞ 时,c((z1-z4)+3(z3-z2))→c(∞)=0,当z3→∞ 时,c((z1-z4)+3(z3-z2))→c(∞)=∞,矛盾。 所以我们有

我们还可以看出c(·)在R上是从∞到0的严格递减的函数。根据定理2可得没有独立性假设下的条件似然函数
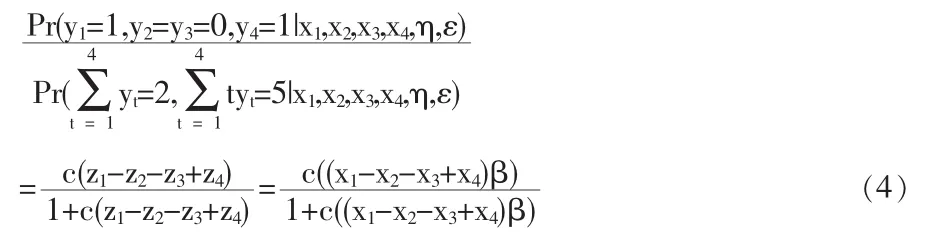
3 结论
本文考察了带趋势的二元面板模型估计问题。对于非线性模型,差分方法已经不再适用。但是由于固定效应模型中固定效应参数会随着个体样本增加而增加,从而利用极大似然估计会出现 “意外参数问题 (incidental parameters prob-lem)”。为此,本文第二部分在随机冲击独立并且其分布是Logistic分布的假设下,证明了对个体固定效应和趋势项系数是充分的。利用这个结果写出了相应的条件似然函数(2)。但是这两个假设太强,本文第三部分放松了这两个假设,并且得到了对个体固定效应和趋势项系数仍是充分的充要条件。据此我们可得到在没有这两个假定的情况下的半参数估计式(4)。
对本文的一个直接推广是解释变量不一定要求是线性组合形式xtβ,一般的形式为ft(xt,β)。这样我们的结果就是非线性函数的差分。如果Matzkin(1992)中条件被满足,ft(xt,β)甚至可以部分未知的。
一个比较困难的问题是带趋势的三期二元面板模型。本文的充分性对三期面板是不适用的。因为在充分性的每个可能取值条件下,yt的值都是确定的,从而条件似然函数都与个体固定效应和趋势项系数无关。考虑三期的一个明显优点是我们可以将一个四期转化为两个三期,从而可能增加信息度,提高有效性。
更困难可能是将这个方法推广到其他模型中去,比如Poisson模型,动态模型(Honore和 Kyriazidou,2000)以及 Tobit类模型估计。
[1]Arellano,M.,B.E.Honore.Panel Data Models:Some Recent Developments[A].In Handbook of Econometrics,Vol.5,ed.By E.Leamer and J.J.Hechman[Z].Amsterdam:NorthHolland,2001.
[2]Chamberlain,G.Analysis of Covariance with Qualitative Data,the Review of Economic Studies,Vol.47,No.1[J].Econometrics Issue,1980,(1).
[3]Honore,B.E.,E.Kyriazidou PanelDataDiscreteChoiceModels with Lagged Dependent Variables[J].Econometrica,2000,70.
[4]Matzkin,R.Nonparametric and Distribution-Free Estimation of the Binary Threshold Crossing and The Binary Choice Models[J].E-conometrica,1992,(60).
[5]Baltige,B.H.Econometric Analysis of Panel Data(3rdedition)[M].Chichester:John Windy&Sons Press,2005.
[6]Magnac,T.Panel Binary Variables and Sufficiency:Generalizing Conditional Logit[J].Econometrica,2004,6(72).
[7]Manski,C.F.Identification of Binary Response Models[J].Journal of the American Statistical Association,1988,(83).

