基于潮波数值模拟技术的潮位推算及其精度验证

缪锦根，刘 雷，董玉磊

（天津海事局海测大队，天津300222）

中国沿海潮波主要是太平洋潮波传入后形成的协振潮，由天体引潮力产生的强迫潮很小，但受地形岸线、海底摩擦、地转偏向力以及浅水效应等因素影响，动力变化巨大，潮汐性质复杂，潮差空间分布悬殊，因此在水深测量的同时必须进行潮位观测，以提供必要的水位改正资料。传统的水位改正方法是在岸上或海上设立验潮站，实行双站分带或三（多）站分区水位改正，有效降低了潮差对测量结果的影响，提高了测深精度，但也存在如下问题：（1）海上及孤岛验潮站设立成本较高，且无精度及完整性保障；（2）要求各验潮站的潮位数据为水深测量期间的同步数据，不能充分利用测区内已有的潮位资料；（3）原则上要求测量区域内潮时、潮差在验潮站之间或控制范围内线性变化。

事实上，实际的潮波运动要复杂得多，没有一定密度的验潮站无法真实地反映测区内的潮波特点。基于余水位空间相关性的潮位推算方法有效地解决了具有历史验潮资料海区存在的前2个问题，而日趋成熟和完善的潮波数值模拟技术使第三个问题的解决成为了可能［1-9］。

1 潮位推算基本原理

潮位推算的基本思想是假设水位由潮汐和非潮汐水位（余水位）2部分构成，并且非潮汐水位具有良好的空间一致性，采用长期验潮站的实测水位剥离潮汐和非潮汐水位部分，并用非潮汐部分改正预报站的潮位。A为长期验潮站，忽略观测误差，水位可表示为

式中：MSLA为验潮站A的平均海面；为天文预报潮位，其中Hi、gi为振幅与迟角，fi、ui为交点因子与交点订正角，v0为天文初相角，σi为分潮角速率；δA（t）为余水位。

2 基于潮波数值模拟技术的潮位推算算法基本流程

（1）对于尺度不大的测区而言，可以通过调试和运行一个二维潮波数值模式，计算测区内网格点主要分潮的调和常数。

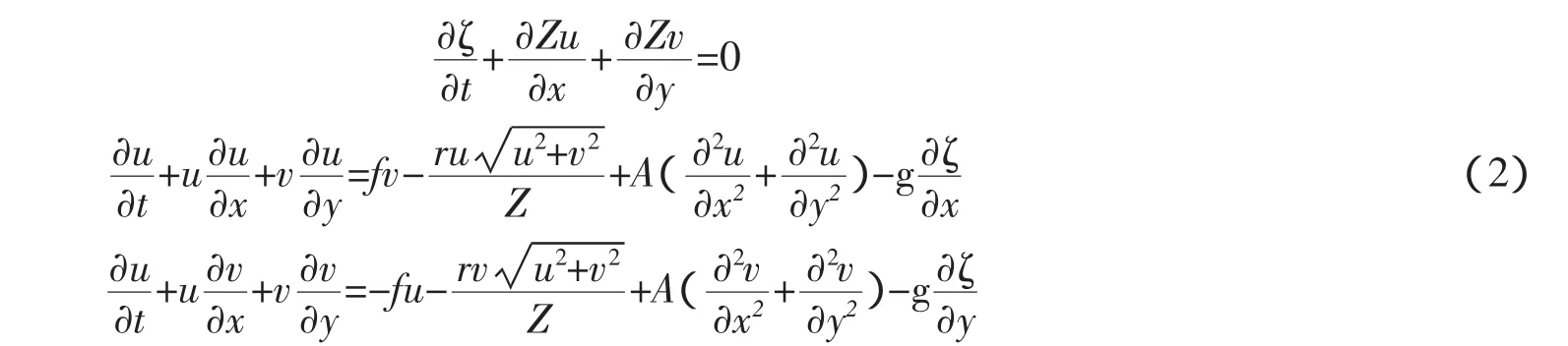
式中：Z=h+ζ，h为从平均海面起算的水深，ζ为潮位，u、v分别为在x方向和y方向的垂向平均流速分量；f为科氏参量；r和A分别为拖曳系数和水平涡动黏性系量；g为重力加速度。数值积分采用已经成熟的方法，如ADI法，开边界潮位可以通过已有的大尺度潮波数值计算结果内插。计算时，从开边界输入的是m1、M2和M4分潮波的合成，其中m1是2个主要全日分潮K1和O1的平均，网格大小为1′×1′。

（2）利用测区内（或附近）长期验潮站资料，分析所有分潮的调和常数（包括反映海面季节变化的长周期分潮调和常数）。

（3）依据测区内长期验潮站的调和常数实测分析结果与数值计算结果的差比关系，对测区内的数值计算结果进行修正。

（4）确定各网格点（1′×1′）的理论最低潮面。理论最低潮面依据（GB12327-1998）《海道测量规范》［2］计算。

（5）利用网格点上的数据，内插计算测区内任意点（x，y）主要分潮的调和常数和理论最低潮面。

（6）利用测区内长期验潮站主要分潮与随从分潮之间的差比关系，将（x，y）的调和常数加以扩展，据此推算该点任意时刻的天文潮位。

（7）利用长期验潮站实测潮位计算给定时刻的余水位（实测水位与天文潮位之差），并据此推算该时刻测区内任意地点（x，y）的余水位。

（8）测区内任意地点给定时刻的潮位是天文潮位和余水位之和。

由基于潮波数值模拟技术的潮位推算方法基本流程可知，影响潮位推算精度的主要因素为天文潮位预报误差和余水位计算误差。天文潮位预报误差取决于测区内数值计算结果精度，要求附近有长期验潮站潮位数据对数值计算结果进行优化；余水位计算误差取决于长期验潮站（余水位控制站）天文潮位计算精度及测区内余水位的空间相关性。天文潮位的预报精度已达到了很高的水平，余水位的计算误差是潮位推算的主要误差源。按照测量规范要求，水深测量一般在较好海况下进行，此时余水位空间差异较小，经验表明，渤海区域100 km范围内，在测区内岸线趋势无明显变化的开阔水域，可用长期验潮站余水位直接代替。

3 应用实例及精度评定

营口港鲅鱼圈港区和仙人岛港区附近有较为丰富的历史水位观测资料，为优化测区内潮波数值计算结果、保证天文潮和平均海面计算精度提供了条件，同时鲅鱼圈海洋站位置适中，地域开阔，具有相当稳定的调和常数，其余水位对整个测区具有较好的可替代性，可作为余水位控制站。

2008年，天津海事局海测大队搜集了营口港附近11个验潮站的历史潮位观测资料，对该区域的数值计算结果进行优化修正，形成了以鲅鱼圈验潮站为余水位控制站，适用于该测区的潮位推算订正系统，系统使用范围为30′×60′。利用历史潮位资料和专门布设的海上验潮站分别对潮位推算结果的内符合精度和外符合精度进行了验证，历史观测资料站点坐标和观测时间见表1，位置分布见图1。

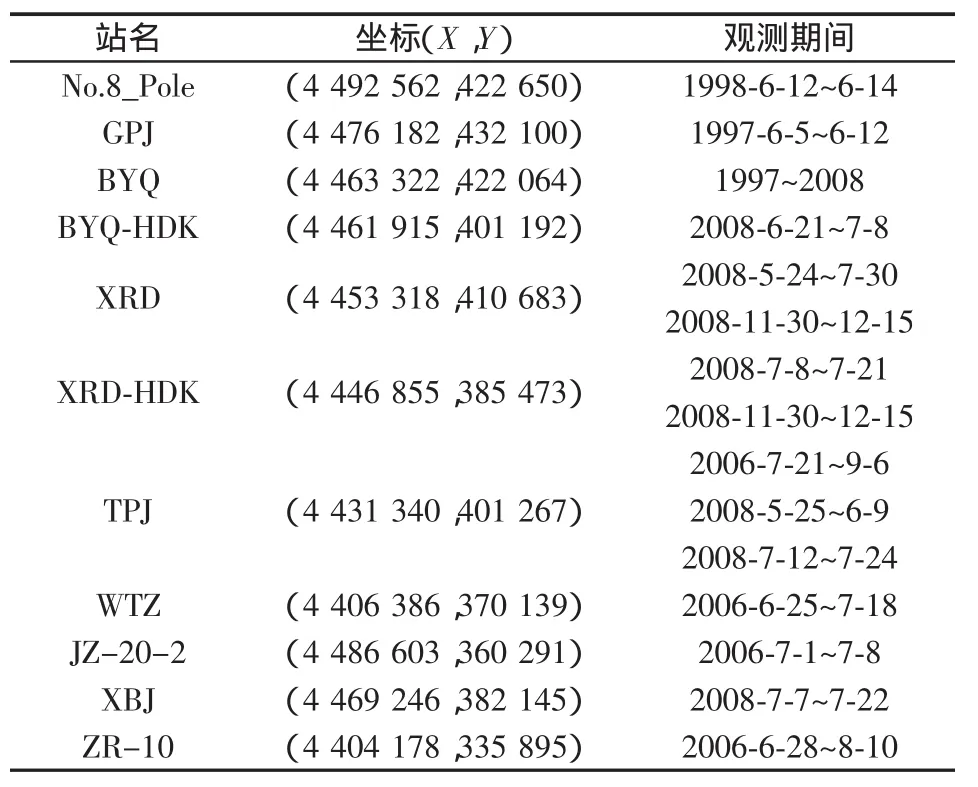
表1 历史资料站点坐标和观测时间Tab.1 Coordinates of history tide data and observation time

3.1 内符合精度

为检验基于潮波数值模拟技术的潮位推算算法的准确性，采用历史上时间较长且数据质量良好的8个验潮站资料分别统计验潮站实测水位与推算水位之间的差值，作为该算法的内符合精度（表2）。

表2 内符合精度统计Tab.2 Statistics of inner accuracy

3.2 外符合精度

为更好地验证营口附近海域潮位推算的实际精度及其稳定性，2009年分别在测区的西北角（RXBJ）和西南角（R-XNJ）附近设立海上定点验潮站，位置坐标和观测时间见表3。

由潮位推算的基本原理可知，基于潮波数值模拟技术的潮位推算算法的计算结果主要包含深度基准面计算误差、天文潮位计算误差和余水位计算误差。RXBJ和R-XNJ观测时间均大于1个月，按照（GB12327-1998）《海道测量规范》要求，借鉴鲅鱼圈验潮站的2个长周期气象分潮可以计算理论最低潮面，其计算结果与数值模拟计算结果比较见表4。

根据潮波数值模拟结果计算2个验潮站深度基准面与按照实测资料分析结果计算的深度基准面差值小于10 cm，满足（GB12327-1998）《海道测量规范》对深度基准面（平均海面）计算精度的要求。

表5统计了验潮站实测水位与推算水位之间的差值，综合反映了平均海面计算误差、天文潮位计算误差和余水位计算误差的影响。

表3 验证软件准确性使用的观测资料Tab.3 Observation data for verifying the software

表4 深度基准面精度比较Tab.4 Comparison for the accuracy of chart datum

表5 外符合精度统计Tab.5 Statistics of outer accuracy

由以上内、外符合精度和深度基准面计算精度的统计结果可以判断基于潮波数值模拟技术的潮位推算应用于水深测量可以满足现行《海道测量规范》对水位改正精度的要求。

4 结论

（1）基于潮波数值模拟技术的潮位推算算法，利用长期验潮站实测余水位订正测深点天文潮位，可以充分利用测区内原有的历史潮位资料，减少临时验潮站的设立，降低了成本，有效减少了因验潮仪进水、零点跳动等因素造成的潮位数值丢失或质量降低。

（2）利用该算法可以推算测区内任何一点的潮位，避免了模型不适用直线分带改正和线性内插改正引起的误差。

（3）计算结果表明在不受径流影响的非河口区域、余水位空间差异不大的水域（岸线趋势无明显变化），应用基于潮波数值模拟技术的潮位推算算法精度较高，可直接应用于海道测量水位改正。

［1］刘雁春.海洋测深空间结构及其数据处理［M］.北京：测绘出版社，2003.

［2］GB12327-1998，海道测量规范［S］.

［3］王征，桑金，王骥.海洋潮位推算在水深测量中的应用［J］.海洋测绘，2002（2）：3-8.WANG Z，SANG J，WANG J.The Application of Tide Level Deduction to the Depth Sounding［J］.Hydrographic Surveying and Charting，2002（2）：3-8.

［4］侯世喜，黄辰虎，陆秀平，等.基于余水位配置的海洋潮汐推算研究［J］.海洋测绘，2005（6）：29-33.HOU S X，HUANG C H，LU X P，et al.Reckoning Rearch Based on Residual Water Level of Tide［J］.Hydrographic Surveying and Charting，2005（6）：29-33.

［5］周华民，谷艺，吕咸青.渤海潮波系统的数值模拟［J］.海洋科学，2005，29（6）：48-52.ZHOU H M，GU Y，LV X Q.Numerical modeling of tidal waves in Bohai Sea and Huanghai Sea［J］.Marine Science，2005，29（6）：48-52.

［6］林晖，闾国年，宋志尧，等.东中国海潮波系统与海岸演变模拟研究［M］.北京：科学出版社，2000.

［7］孟德润，田光耀，刘雁春.海洋潮汐学［M］.北京：海潮出版社，1993.

［8］方国洪，郑文振，陈宗镛.潮汐和潮流的分析和预报［M］.北京：海洋出版社，1986.

［9］陶本藻.测量数据统计分析［M］.北京：测绘出版社，1992.