防波堤堤后次生波的试验研究

戈龙仔，迟 杰，张慈珩

（交通部天津水运工程科学研究所工程泥沙交通行业重点实验室，天津300456）

随着经济的发展，港口工程建设规模不断扩大，波浪物理模型试验所涉及的工程水域也逐渐加大。由于试验条件、精度的限制，采用单一模型试验往往不能完全解决工程问题，需同时采用数值模拟和大范围物理模型试验研究手段。尤其遇到工程中需解决不同水位、不同方向波浪作用下波浪越过防波堤后，对码头前沿处波高分布和上水的影响，确定防波堤堤顶高程等工程问题。由于研究采用比尺小的大范围整体物理模型试验，模型本身存在底摩阻和比尺效应等因素的影响，测量波浪越堤形成的堤后生次生波精度较低，同时目前数值模拟所采用的计算软件也难以模拟波浪越过防波堤的整个破碎过程，各种参数调整仍只是经验性。国内外进行了很多堤后次生波的研究，影响次生波的因素较复杂，包括堤顶宽度、坡度、护面型式等，另外次生波堤后的传播与水深地形也有关，本文通过大比尺波浪断面物理模型试验（断面的护面块体采用扭王字块），选取不同入射波要素和堤顶淹没水深，研究波浪越过堤顶后形成新的波列即次生波的基本特性，得到入射波高与次生波关系以及沿程衰减的规律（试验中断面后地形采用同一高程）；同时利用局部整体模型试验，得出波浪对防波堤不同角度入射时，角度与堤后次生波关系。成果可为大范围整体物理模型试验提供校验依据，为防波堤堤顶越浪数学模拟的参数调整提供依据。

1 试验概述

断面物理模型试验在交通运输部天津水运工程科学研究所试验水槽中进行，水槽长70 m，宽1 m，高1.3 m，水槽两端均设有消波装置，水槽底部设有连通管，以保证造波过程中模型两侧的水位保持不变。半整体物理模型试验在工程泥沙交通行业重点实验室40 m×80 m港池中进行。造波机为电机伺服驱动推板吸收式造波机，可以产生规则波与不规则波，波高采用SG2000型动态水位测量系统。

模型按重力相似准则设计制作，断面物理模型试验选用几何比尺λ=30，力比尺为λF=27 000，时间比尺为λt=5.48。半整体物理模型试验选用几何比尺λ=80，时间比尺为λt=8.94。不规则波波谱采用JONSWAP谱［1］。试验中采用不同入射波要素与堤顶淹没水深，研究波浪越过堤顶后形成新的波列即次生波的基本特性，得到入射波高与次生波关系，试验波要素见表1。为测定越浪产生的堤后次生波和沿程衰减规律，试验在防波堤堤后水槽中不同距离处布置29个波高传感器（传感器间距离均为30 m）。

表1 试验波浪要素Tab.1 Wave parameters of model test

试验断面一泥面高程为-6.0 m，堤顶高程为-1.0 m，断面内侧、外侧均采用3.0 t扭王字块护面，断面结构见图1-a；试验断面二泥面高程为-1.9 m，堤顶高程为+5.5 m（对比高程+5.0 m、+4.5 m）。堤顶结构为挡浪墙型式，海侧采用4.0 t扭王字块和不同尺寸栅栏板护面，港浪侧均为不同尺寸栅栏板护面，断面结构见图1-b。

图1 防波堤各断面结构详图Fig.1 Sketch of cross-sections of breakwater

2 试验结果及分析

2.1 堤后次生波沿程分布结果

试验结果表明，不同堤顶淹没水深时堤后形成的波浪形态不同，当为潜堤时，波浪均越过堤顶，至堤后发生破碎，破碎后形成新的波列继续向前传播；当为出水堤时，波浪在堤顶破碎形成新的波列向后传递。堤顶不同淹没水深时，波浪作用下的堤后次生波高沿程分布结果见图2。

由图2堤后次生波沿程分布结果来看，可将越堤后的波浪形态大致描述为3个不同区段：第一区段为波浪成长区，范围从堤顶到堤后0.25 L（L为波长，下同），波浪在潜堤顶发生显著浅水变形，使局部产生壅水，波高增大，表现为堤后第一个测点次生波波高Ha大于入射波高Hi，即Ha/Hi大于1.0；第二区段为波浪破碎区，范围为堤后4 L以内，当波高增大至一定程度，波峰变尖，波形前缘变陡，随后在波前沿根部发生剧烈破碎，此时水体表面紊乱，波能迅速耗散，波高减小（见图2中4 L范围内波高减小）；第三区段为波浪水质点调整区，范围为4 L以后，波浪水质点垂向调整完成后，剩余的波能形成新波高和周期组成波列继续向后传递，此时波高沿程传播主要是浅水变形，波高沿程衰减不明显（见图2中4 L～15 L波高衰减过程）。

2.2 堤顶相对水深与堤后次生波分析

2.2.1 对次生波波高、周期的影响

图2 不同堤顶水深时堤后次生波高沿程分布Fig.2 Distribution of secondary wave height along the way with different water levels above levee crest

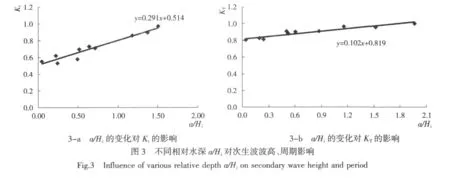
（1）波高影响分析：波高透射系数Kt是研究波浪越堤形成次生波的一个重要指标，定义为堤后次生波波高与入射波高之比，即Kt=Ha/Hi。考虑堤顶水深a的影响时，采用无因次量相对堤顶水深a/Hi进行分析［2］。试验选用有效波高的波高H1/3透射系数Kt与相对堤顶水深a/Hi的关系进行研究。以a/Hi为横坐标，以Kt为纵坐标，a/Hi对Kt的影响如图3-a所示。由图3-a明显看出，Kt值随着a/Hi的增大而增大，并且逐渐接近Kt=1。Kt和a/Hi在规律上有明显的线性关系，拟合经验公式为

式中：a/Hi有一定范围限制，当a/Hi＞1.4时，堤后次生波的波高值变化很小，取Kt=1。

为验证试验得出波高透射系数拟合公式的适用性和合理性，进行试验结果与规范公式［3］结果比较（表2）。从表2可知，两者存在差异，主要原因为规范公式计算结果的条件为试验断面采用抛石护面，本次试验得出结果断面采用扭王字块护面，而护面型式对堤后次生波存在影响。从结果来看两者总的趋势相同，随着堤顶相对水深的增加，波高透射系数增加。

表2 波高透射系数Kt对比结果Tab.2 Contrast of wave height transmission coefficients

（2）周期影响分析：入射波越过堤顶后破碎形成新的波列，其周期也将发生相应的变化。因此与波高分析方法相同，定义周期变化系数KT为次生波周期与入射波周期之比。用公式表示为KT=Ta/Ti，也同样采用无因次量a/Hi和KT进行分析，结果见图3-b。由图3-b中可以看出，周期变化因子KT与相对堤顶水深a/Hi表现出一定的规律，KT随着a/Hi的增大而增大，拟合经验公式为

2.2.2 对次生波波谱的影响

对于越堤后形成新的波列，其波谱产生的变化见图4，从图4中能够看出波浪越过防波堤堤后，谱峰值明显减小。可采用谱参数直观的反映波谱的改变［4］，与波高和周期分析方法相同，定义波能透射系数Km0=m0′/m0（m0为波浪谱的零阶矩）；定义谱峰值折减系数KS为次生波谱峰值与入射波谱峰值之比，用公式表示为

图4 入射波和次生波波谱对比Fig.4 Contrast of incident wave and secondary wave spectrum

由图5-a看出，波能透射系数随着相对堤顶水深a/Hi的增大而增大，当a/Hi增大到一定程度后，波能透射系数增大的速度逐渐变小，慢慢趋近于Km0=1，拟合得到经验公式

由图5-b看出，谱峰值Sfp的变化很大，次生波的谱峰值比入射波的谱峰值要小，总体上来说，随着a/Hi的增大，谱峰值折减系数KS逐渐增大，拟合得经验公式

图5 不同相对水深a/Hi对次生波波谱的影响Fig.5 Influence of various relative depth a/Hion secondary wave spectrum

3 不同角度的入射波对堤后次生波影响分析

由波浪断面物理模型［5］及防波堤局部整体物理模型试验［6］堤后次生波结果，分析防波堤在不同入射角度（分别为 0°、10°、20°、30°、40°、50°）下，堤后次生波的波高与入射角度的关系，得出入射角度不同对堤后次生波大小的影响规律；分析中引入次生波高与入射波高的比值K，且将每个角度波浪作用所得到的Ki值与0°时K值进行对比，定义影响系数r=Ki/k，对比结果见表3和图6。从对比结果可知：当入射角度β≤10°时，与正向入射比较，斜向入射减小不明显，甚至略有增大；当β＞20°时，堤后次生波随波向角的增大而减小；β=50°时，堤后次生波比正向波减小幅度在40%～50%。

表3 不同入射角度次生波波高影响结果Tab.3 Secondary wave heights of different incident angles

4 结论

通过对防波堤断面在不同入射波高和堤顶淹没水深的波浪物理模型试验，得到以下结论：（1）各断面堤后形成的次生波波高随着堤顶淹没水深、入射波高的增大而增大，但沿程衰减变化趋势基本相同，随着距离的增大而变小，且主要集中在堤后4 L范围内，4 L以外则衰减变慢。（2）堤后次生波周期的变化与堤顶水深有关，也随着相对堤顶水深值的增大而增大。（3）堤后次生波的波谱变化规律为：总的波能小于入射波，但波能透射系数和谱峰值折减系数随着相对堤顶水深值的增大而增大。（4）不同角度入射对堤后次生波影响为：当入射角度β≤10°，堤后次生波波高与正向比较，变化不明显甚至有前者大于后者的情况；当β＞20°时，堤后次生波波高随波向角的增大而减小；当β=50°时，斜向作用得到堤后次生波波高仅为正向作用时的0.4～0.5倍。

［1］JTJ213-98，海港水文规范［S］.

［2］谢世楞，蔡艳君.半圆形潜堤后的波高分析［J］.港工技术，1999（4）：1-3.XIE S L，CAI Y J.Analysis of Wave Heights Behind a Submerged Semi-Circular Breakwater［J］.Harbor Technology，1999（4）：1-3.

［3］JTJ298-98，防波堤设计与施工规范［S］.

［4］康万军，陈汉宝，唐文帅.潜堤次生波波高规律的试验研究［J］.水道港口，2009（5）：336-341.KANG W J，CHEN H B，TANG W S.Experimental study on secondary wave height over submerged breakwater［J］.Journal of Waterway and Harbor，2009（5）：336-341.

［5］戈龙仔，康万军，迟杰.黄骅港综合港区起步工程波浪断面物理模型试验研究［R］.天津：交通部天津水运工程科学研究所，2009.

［6］张慈珩，陈汉宝，迟杰.北堤越浪局部整体物理模型试验研究［R］.天津：交通部天津水运工程科学研究所，2009.