两轴稳定平台的模糊－PID复合控制器设计与仿真

李向旭，张曾科，姜 敏

(1.清华大学自动化系，北京 100084;2.苏州大学电子信息学院，江苏 苏州 215021)

0 引言

两轴光纤陀螺稳定平台的主要作用是稳定雷达天线指向和跟踪目标移动［1］。根据两轴雷达稳定平台的结构和原理［2－3］，如果平台机械结构设计合理，就可以保证两个通道之间的影响很小［4］，这样就可以忽略两个通道之间的耦合。本文只讨论俯仰通道控制器的设计。光纤陀螺作为速度测量元件与稳定回路控制器Cs(s)、速度内环和减速器闭环构成稳定回路。角位置传感器作为角位置测量元件，与跟踪回路控制器Cp(s)、稳定回路和积分模块闭环构成跟踪回路。

1 经典控制器设计及仿真

由于所用电机的电枢电路总电感非常小，可以忽略电机电气时间常数。根据电机方程，得到电机传递函数为

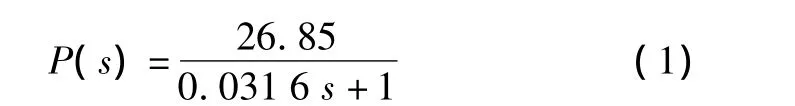
则速度内环的传递函数为

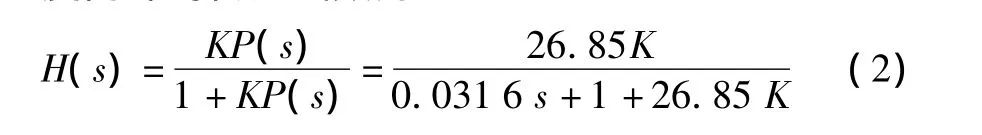
其中:K为放大环节的放大倍数，根据经验取K=20。

1.1 稳定回路经典控制器设计及仿真

根据实际工作要求，稳定回路开环截止频率在200 rad/s左右，隔离度要求为If=0.5Hz<0.5%，If=1Hz<1%，If=3Hz<5%，f为外加干扰的频率［5］。

根据以上要求，采用滞后超前校正法设计稳定回路 PID 控制器［6］:

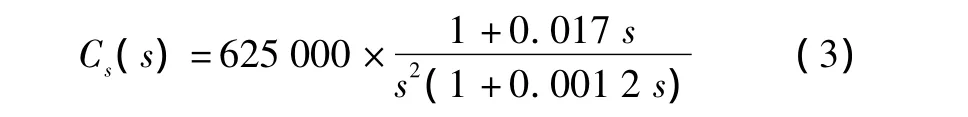
加入此控制器后，系统稳定回路开环截止频率为206 rad/s，相角稳定裕度为59.2°，幅值稳定裕度为38.2 dB。稳定回路是稳定的，开环截止频率满足要求。由图1的Simulink模型仿真可得If=0.5Hz=0.08%，If=1Hz=0.35%，If=3Hz=2.8%，即稳定回路控制器(3)满足系统性能要求。

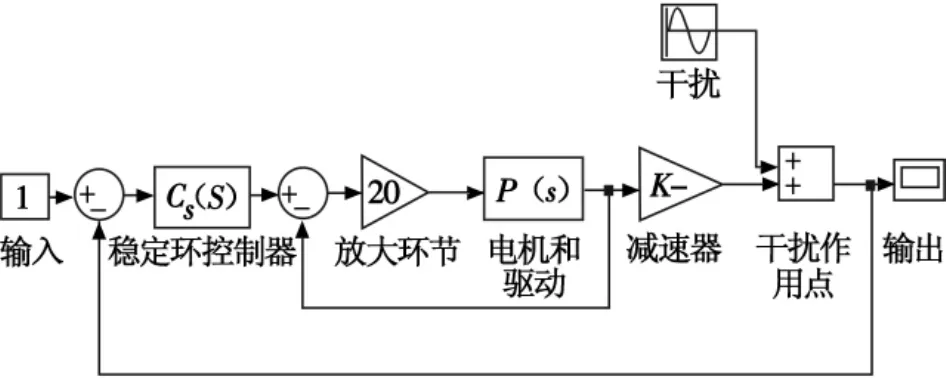
图1 稳定回路仿真模型Fig.1 Simulation model for the stable loop

1.2 跟踪回路经典控制器设计及仿真

跟踪回路的输入为目标视线方向(LOS)角位置，稳定平台必须能够快速准确地跟踪它的变化。实际系统要求单位阶跃输入响应超调量σ<25%，过渡过程时间ts<0.2 s，稳定误差e(∞)=0，震荡次数 N≤2。为了避免引入高频干扰，要求跟踪回路开环截止频率ωc≈50 rad/s。

采用滞后超前校正方法设计跟踪回路PID控制器:

加入Cp(s)后跟踪回路开环截止频率为wc=54.2 rad/s，相角稳定裕度为49.7°，幅值稳定裕度为12.7 dB。跟踪回路控制器(4)满足跟踪回路必须稳定的要求。然而，跟踪回路的单位阶跃响应为图2所示的PID响应曲线，系统的超调量σ=28%，过渡过程时间ts=0.145 s。系统阶跃响应的超调量超出了设计要求的范围。因此，必须在保证开环截止频率不变的基础上降低阶跃响应超调量。

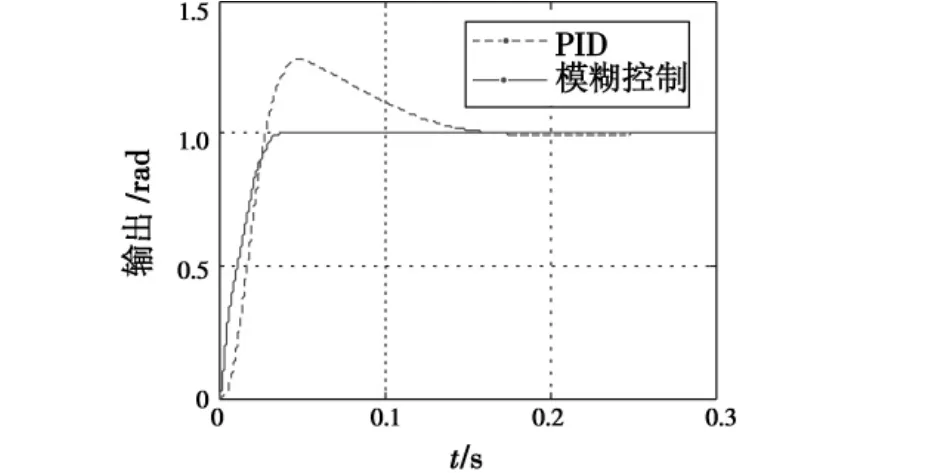
图2 PID控制和模糊控制单位阶跃响应Fig.2 Unit step responses of the PID controller and fuzzy controller

2 遗传算法设计位置模糊控制器

2.1 模糊控制器的结构

为了解决1.2节中系统超调量过大的问题，本文进一步采用两维模糊控制器［7－8］。模糊控制器的输入为误差e和误差的变化率ec，相应的量化因子分别为ke和kec。线性变换E=kee将变量e从语言的基本论域映射到量化论域E。当kee>6时，令E=6;当kee<－6时，令E=－6。定义在量化论域E上的模糊子集为{NB，NM，NS，O，PS，PM，PB}，其隶属度函数如图 3所示。EC=kecec与上述定义相同。EC和U上定义的模糊子集和各个子集对应的隶属度函数与E相同。

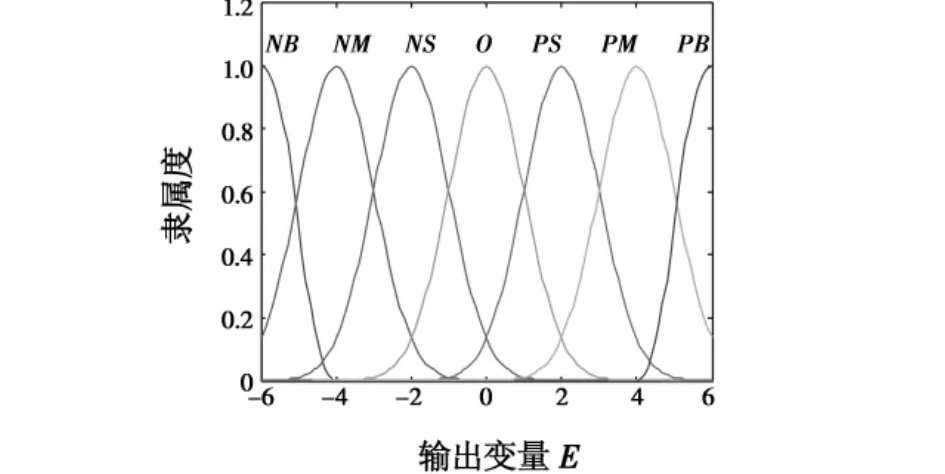
图3 模糊控制器输入变量的隶属度函数Fig.3 Membership function of the input variable of the fuzzy controller

模糊规则表详见文献［9］中表5－1。模糊推理采用Mamdani准则，输出模糊量逆模糊化采用加权平均法，模糊控制器输出u=kuU。

2.2 遗传算法优化位置模糊控制器参数

遗传算法是一种模仿生物进化的智能算法，部分学者利用遗传算法解决了模糊控制器设计问题［10－11］。本文用遗传算法来优化跟踪回路模糊控制器ke、kec和ku3个参数。对于稳定平台而言，单位阶跃输入为最苛刻的输入，因此只对单位阶跃输入时的系统进行优化。

种群数量20，采用实数编码法。选择策略采用排序选择法，同时采用保留最佳个体的机制，使适应度函数最小的两个个体保留到下一代。交叉操作采用算术交叉法，交叉概率为0.8。交叉操作采用非均匀变异法，变异概率为0.01。适应度函数:

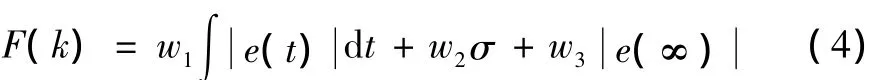
式中:e(t)为t时刻的误差值;σ为系统阶跃响应的超调量;e(∞)为系统响应的静态误差;w1、w2、w3为大于零的权重值，取 w1=10、w2=200、w3=5000。

进行50代的迭代后，得到ke=17.918、kec=0.138和ku=111.771。每一代中最优的适应度函数变化曲线如图4所示。

系统单位阶跃响应如图2中模糊控制响应曲线所示。模糊控制器可以很好地改善系统的响应特性，不仅使系统的超调量为零，而且可以将系统的过渡过程时间控制在0.15 s以内。然而，模糊控制的阶跃响应存在0.2%的静态误差，而且无法直观地得到跟踪回路的开环截止频率，难以保证其在50 rad/s左右。

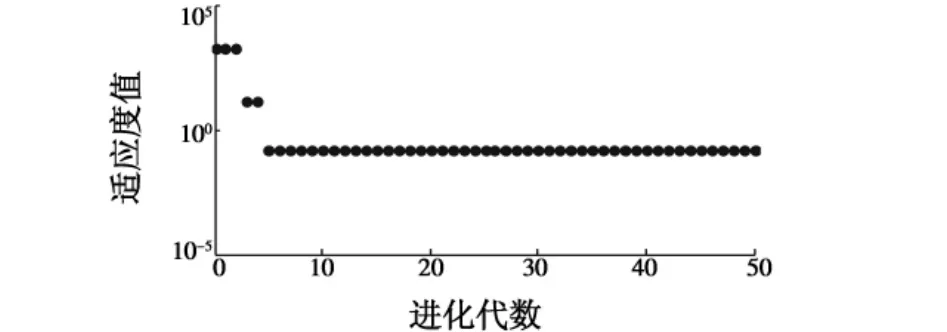
图4 遗传算法优化最优适应度变化图Fig.4 Best fitness values of the GA

3 模糊调整加权的模糊－PID复合控制器设计与仿真

由第1节和第2节可知，单纯的PID控制和遗传算法优化的模糊控制都不能完全满足系统的要求，因此必须把两者结合起来形成复合控制器。常用的结合方法是阈值切换法，其基本思想是:当误差绝对值大于设定阈值时，采用模糊控制策略，当误差绝对值小于设定阈值时采用PID控制策略［12］。但是在切换时刻两种控制器输出一般不相等，这容易造成施加给被控对象的控制量发生跳变，造成系统震荡［13］。本文采用模糊控制调整加权因子的PID－模糊复合控制策略来解决这个问题。

3.1 复合控制器的设计

设计复合控制器输出为

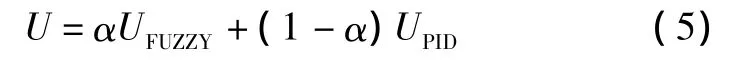
式中:UFUZZY为模糊控制器输出;UPID为经典控制器输出;α为模糊控制器和经典控制器输出的加权因子，并且0≤α≤1。

本文采用一维模糊控制器来计算α，其输入为系统误差，其变化范围为［－1，1］，输入变量量化因子为ke′=6，则误差的量化论域为［－6，6］。定义在误差量化论域上的模糊子集为{NB，NM，O，PM，PB}，相应的隶属度函数如图5所示。

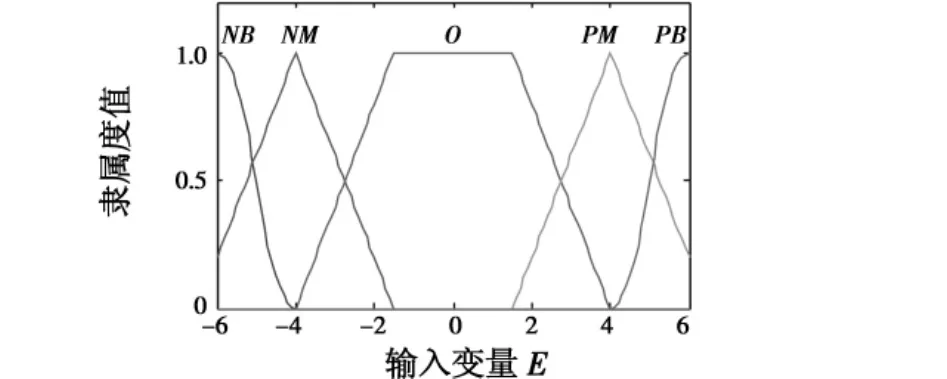
图5 加权因子模糊控制输入变量的隶属度函数Fig.5 Membership function of the input variable of the weighted factor fuzzy controller

模糊控制规则如下:

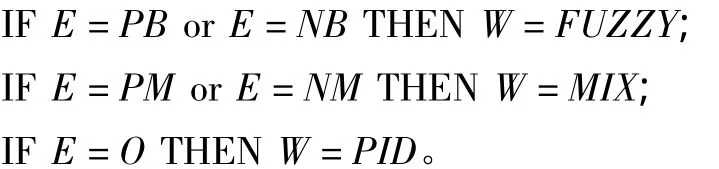
输出变量W的模糊子集为{PID，MIX，FUZZY}，其隶属度函数如图6。

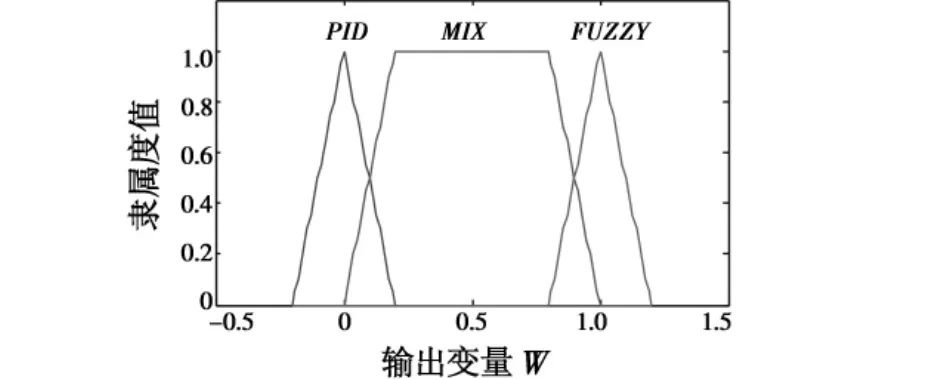
图6 加权因子控制器输出变量的隶属度函数Fig.6 Membership function of the output variable of the weighted factor fuzzy controller

模糊推理采用了Mamdani准则，逆模糊化采用加权平均法。输出变量的比例因子为1，即α=W。加权因子模糊控制器的输入和输出关系如图7所示。当误差绝对值|e|<0.167时α=0，复合控制器就是经典PID控制器Cp(s);α随着误差绝对值增大而增大，复合控制器输出越来越多地依赖于模糊控制器输出;α随着量化误差变化连续变化，复合控制器输出不会产生较大突变，避免了由阈值切换法引起的输出震荡。

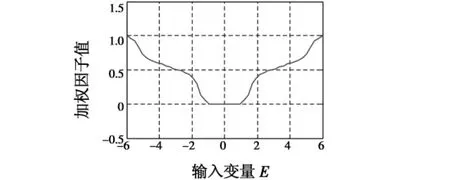
图7 加权因子模糊控制器输入输出关系Fig.7 The input-output relationship of the weighted factor fuzzy contoller

3.2 仿真结果

图8所示为系统跟踪幅值为1，周期为0.5 s，脉宽为0.25 s的方波信号的响应曲线。可见，复合控制器具有比单纯PID控制器更好的跟踪性能。0 s至0.25 s的复合控制响应曲线可以看作系统的单位阶跃响应曲线。复合控制的单位阶跃响应的超调量为16%，过渡过程时间为0.145 s，静态误差为零。

如果在输入端输入斜率为1的斜坡信号，则系统跟踪的误差曲线如图9所示。单纯的PID控制和复合控制的跟踪误差曲线重合，即两者具有相同的跟踪精度。误差绝对值|e|<0.167，如3.1节所述，复合控制器就是经典PID控制器Cp(s)，所以复合控制器和经典PID控制器有相同的静态误差，跟踪回路开环截止频率约为50 Hz。

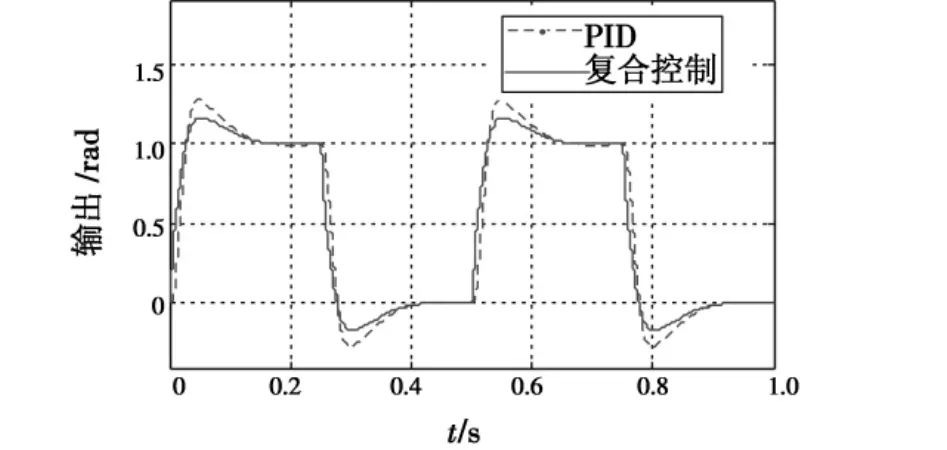
图8 PID控制和复合控制单位方波跟踪响应Fig.8 The square wave responses of the PID controller and the composite controller

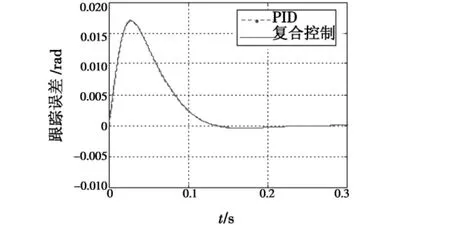
图9 PID控制和复合控制单位斜坡信号跟踪误差曲线Fig.9 Ramp signal tracking error curves of the PID controller and composite controller

如果在系统输出端加上宽度为0.1 s，周期为0.2 s，幅值为0.3 rad的正负交替的干扰脉冲。PID控制器和复合控制器响应曲线如图10所示。可见，与单纯的PID控制相比，复合控制具有更强的抗干扰能力。

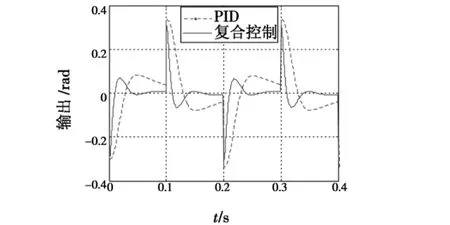
图10 PID控制和复合控制方波干扰响应Fig.10 Square wave disturb responses of the PID controller and the composite controller

4 结论

仿真性能表明，文中设计的模糊控制调整加权因子的模糊－PID复合控制器可以满足系统的要求。从设计过程而言，PID控制器和模糊控制器可以根据系统要求独立设计，简化了设计工作。与模糊PID算法相比，这种方法比较简单，需要的计算量较小。

模糊－PID复合控制器设计的核心是寻找最优的系统误差和加权因子之间的对应关系，而加权因子模糊控制器的输入输出模糊变量的隶属度函数和量化因子决定了这种对应关系。在进一步研究中可以采用模糊神经网络在在线运行中调整有关参数来优化系统性能。

［1］RUE A K.Stabilization of precision electro-optical pointing and tracking systems［J］.IEEE Trans Aerospace and Electronic Systems，1969，AES-5:805-819.

［2］唐小军，赵晓蓓，毛武军.基于DSPs的空空导弹位标器控制系统的设计［J］.弹箭与制导学报，2005，25(2):327-332.

［3］陆岷，张平.基于DSP的天线稳定平台控制器［J］.计算机测量与控制，2006，14(8):1052-1071.

［4］MCKERLEY C W.A model for a two degree of freedom coupled seeker with mass imbalance［C］//Southeastcon’96，‘Bring Together Education，Science and Technology’，Proceedings of the IEEE，11－14 April，1996:84-87.

［5］赵超.导引头稳定系统隔离度研究［J］.电光与控制，2008，15(7):78-82.

［6］孙宁，刘洁瑜，周小刚，等.光纤陀螺惯性数字稳定回路设计［J］.电光与控制，2007，14(3):131-135.

［7］车宏，卢广山.模糊控制在机载光电跟踪系统中的应用［J］.电光与控制，2001，8(4):15-20.

［8］何华锋，胡昌华，代延民.一种自适应模糊PID控制器应用仿真［J］.电光与控制，2006，13(1):41-44.

［9］李士勇.模糊控制和智能控制理论与应用［M］.哈尔滨:哈尔滨工业大学出版社，1990.

［10］欧阳晋，屈卫东.基于遗传算法的模糊控制器优化设计及应用［J］.控制与决策，2003，18(2):386-388.

［11］FANG Laihua，WU Aiguo，ZHENG Aihong.GA＆LS-based fuzzy neural network control［C］//Proceedings of the 5th World Congress on Intelligent Control and Automation，2004:2467-2650.

［12］薛福珍，刘忍权.基于GA的模糊－PID控制器设计［J］.自动化与仪表，2006(3):45-49.

［13］姬伟.陀螺稳定光电跟踪平台伺服控制系统研究［D］.南京:东南大学，2006.