跨音速大攻角电视制导炸弹绕流流场数值分析

于 雷，滕 鹏，鲁 艺，周志刚

(空军工程大学工程学院，西安 710038)

0 引言

在现代生产设计和科学研究中，实验研究与数值模拟是两个重要的手段，二者相辅相成。尤其是在航空航天及武器系统的设计研究中，存在着许多可以通过数值模拟来解决的问题，诸如飞行器复杂流场及气动力、飞行器与外挂分离气动干扰等［1］。通过对这些问题的数值模拟，可以更加深刻地理解问题产生的机理，为实验研究和结果整理提供指导，节省实验所需的大量的人力、物力和时间。Fluent是一款基于有限体积法，集网格生成、流场求解、数据可视化等于一体的国内外使用最广泛的商用计算流体动力学(CFD)分析软件系统;Gambit作为Fluent的前处理软件，可以读入多种CAD软件的三维几何模型和多种CAE软件的网格模型［2］。

某型航空子母弹是一种用于对付地面集群目标、封锁机场跑道、电站电线的对地攻击武器，其母弹采用的是某型电视制导炸弹。本文以该电视制导炸弹(以下简称炸弹)的外形为基础，应用CFD的相关理论、方法以及软件，对炸弹在亚、跨、超音速以及不同攻角条件下的三维流场进行数值模拟，对不同工况下的三维流场结构特性以及炸弹气动特性进行分析研究。

1 仿真建模及网格生成

利用Gambit 2.2软件对该炸弹以及绕流流场进行三维建模，设置边界类型并进行网格划分［3］。炸弹表面网格如图1所示，整个流场计算区域网格划分如图2所示。

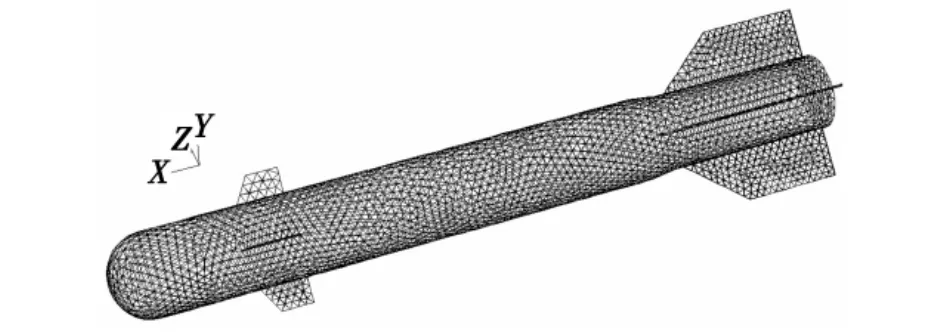
图1 母弹外形尺寸及表面网格Fig.1 The three-dimensional shape and surface grid of TV-guided bomb

图2 三维绕流流场及网格划分Fig.2 Three-dimensional grid models of the flow field

划分网格时采用混合网格技术［2，4－5］，即在弹头部及流动规律复杂的弹体周围区域采用半结构网格并且网格布置得较密集，而在远离弹体流动较稳定的区域采用非结构网格并且网格布置得较稀疏，这样生成速度较快，生成质量也比较高。最终划分网格总数为267997，没有负网格，而且正交性、长宽比、扩展比都达到一定要求。根据流体力学的相似性理论［6］，可以通过改变来流的方向，使之与炸弹成相应的夹角，便可实现炸弹具有一定攻角飞行的绕流流场数值模拟，并不需要改变炸弹姿态与模型，以及整个流场的网格结构。

2 计算模型与计算方法

2.1 控制方程

积分形式的 Navier－ Stokes方程为［2，4－5］

式中:矢量H为源项;ρ为密度;u、υ、w为时均速度;E为单位质量的总能;p为流体压力;τ为粘性应力张量;q为热流通量;A为表面面积矢量。

单位质量总能E与总焓H的关系为

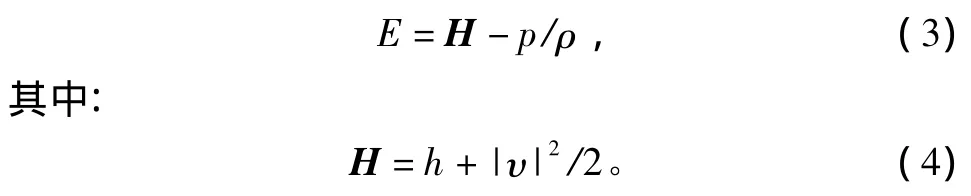
2.2 湍流模型

湍流模型为标准 k－ε 两方程模型［2，4－5］，湍流动能k及其耗散率ε从下列输运方程得到:

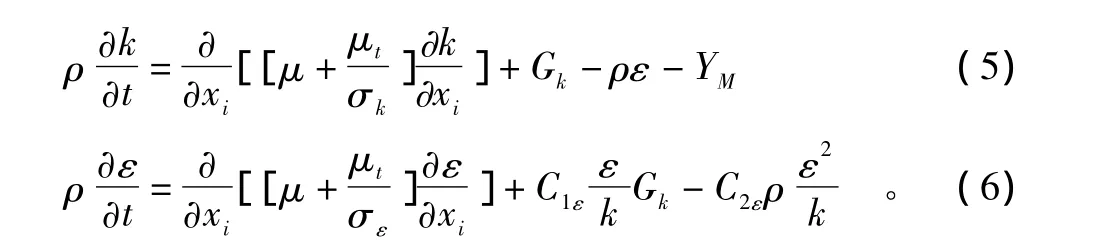
方程中Gk代表由平均速度梯度引起的湍动能生成项;YM是可压缩性影响项;C1ε和 C2ε是常量;σk和 σε分别是k和ε的湍流普朗特数。

2.3 定解条件和初始条件

方程差分求解的定解条件以及初始条件如下［7－9］:1)来流边界条件，对于超音速入口，给定无穷远来流条件;对于亚音速入口，给定来流的总压和总温边界条件;2)下游边界条件，对于超音速出口，边界条件采用外推;对于亚音速出口，给定出口压力;3)边界条件，物面边界采用绝热壁假设和无滑移条件，并且速度采用无穿透条件;外边界取压力远场边界条件;4)初始条件，整个初始流场采用无限远来流。

2.4 计算方法

采用耦合求解法，在求解连续、动量和能量方程的基础上分别求解其他的标量方程。应用Gauss－Seidel迭代法求解由有限体积法离散基本控制方程组得到的代数方程组［2，4］，为了便于收敛和满足计算精度对控制方程各量采用二阶差分格式，对湍动能及其耗散率采用一阶差分格式。本文采用Fluent 6.2软件求解控制方程，完成对炸弹三维绕流流场的数值模拟，其中物性参数及湍流模型参数采用默认值［3］。

3 数值模拟与结果分析

3.1 流场数值分析

对炸弹三维绕流流场进行数值模拟，得到来流马赫数Ma=0.7～1.4，攻角α=0°～15°时的流场静压力分布图、温度分布云图、马赫数分布图分别如图3～图11所示。其中计算来流符合标准大气条件，气温T=288.15 K。

由图3～图5可知，当来流马赫数Ma=0.8，在炸弹头部形成一个高压区，在炸弹头部与圆柱部连接处气流发生膨胀，该处的马赫数亦相应增大;在弹体表面由于空气的粘性而形成摩擦阻力，其能量损失转化为内能从而使得弹体以及附面层的温度升高;在炸弹底部形成一个低压区，由于周围空气向底部补充时流动非常紊乱，产生许多小的漩涡形成底部涡流，气流速度的大小与方向在此区域均发生较大变化，大部分能量转化为涡流的动能和内能使得尾部温度升高尤为显著;流场内无激波产生。进一步的数值模拟表明，在亚音速范围内炸弹绕流流场有相似的结构形式。

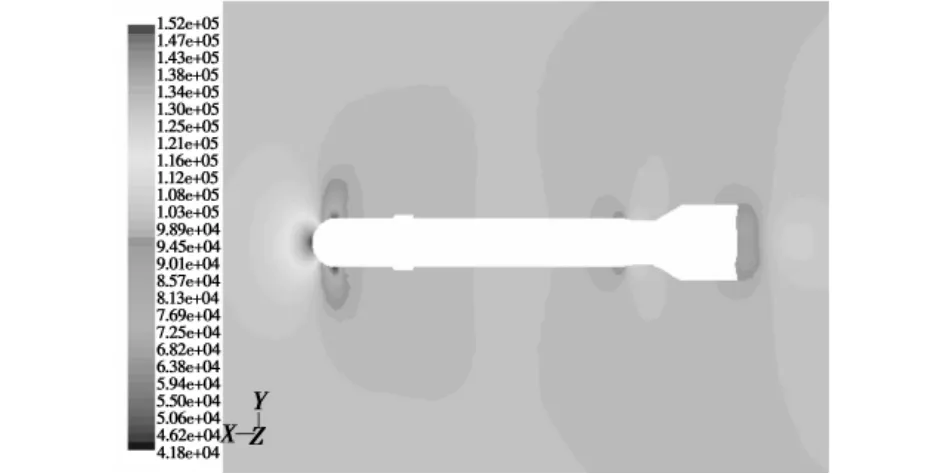
图3 静压分布图(Ma=0.8，α=0°)Fig.3 The pressure distribution(Ma=0.8，α =0°)

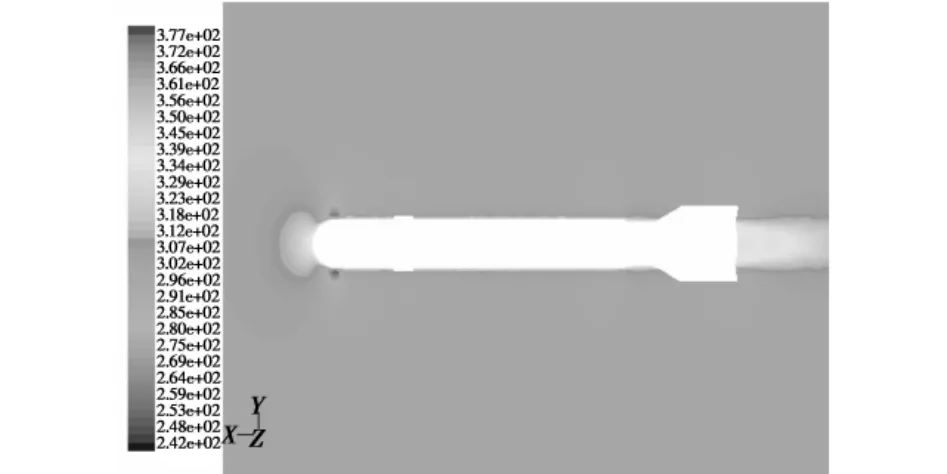
图4 温度分布图(Ma=0.8，α=0°)Fig.4 The temperature distribution(Ma=0.8，α =0°)

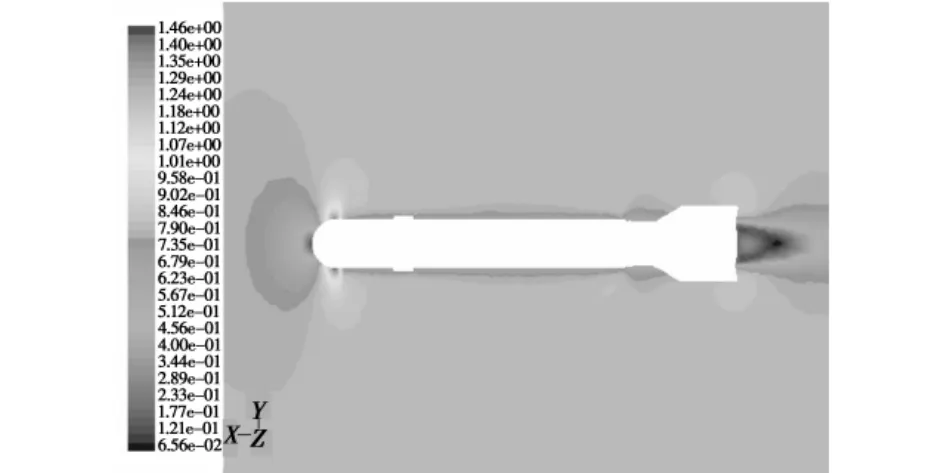
图5 马赫数分布图(Ma=0.8，α=0°)Fig.5 The mach number distribution(Ma=0.8，α =0°)

分析图6～图11可知，在跨音速条件下(来流马赫数Ma=1.0、1.1)，当前方空气流到激波面上时，其压强突然增大，必然使得被压缩的空气温度突然升高、内能增大，激波阻力所消耗的动能转化为空气内能;并且由于表面摩擦和底部涡流的原因使得弹体周围和炸弹底部的温度升高，尤其是后者温度升高更为显著。在马赫数较小时(Ma=1.0、1.1)，炸弹头部产生脱体正激波，随着马赫数的增大(Ma=1.2)，激波角逐渐减小;在炸弹底亦有尾部激波存在，并且随着马赫数的增大(Ma>1.2)，激波倾斜角亦逐渐减小。同时，当来流马赫数Ma>1.2，在炸弹头部与圆柱部连接处、炸弹尾部有两道膨胀波产生(如图9～图11所示)，这是由于超音速气流流过上述连接处后发生膨胀、加速所致，使得两处气流的密度减小，压强下降，温度下降，流速增大;并且随着马赫数的增大，膨胀波角度亦逐渐减小。如图6～图8所示，当来流与炸弹之间具有一定攻角时，所产生的激波与膨胀波发生相应的倾斜，并且其强度也会在背风面与迎风面产生不同的差异。

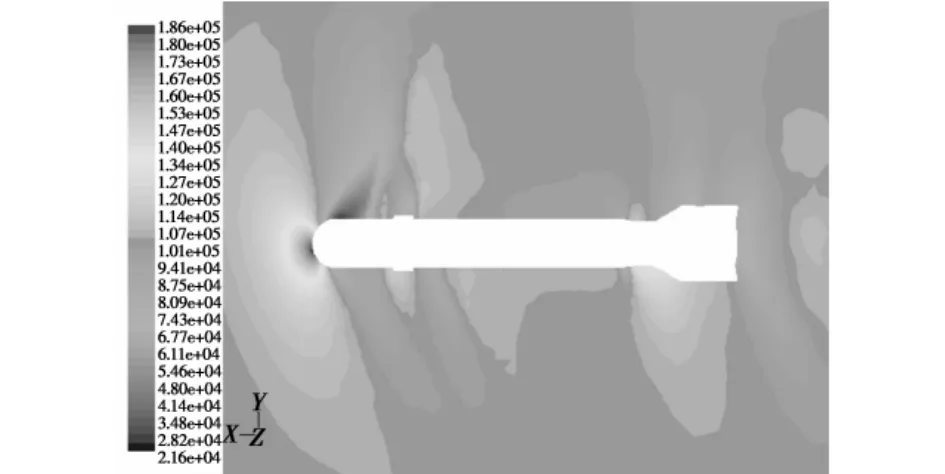
图6 静压分布图(Ma=1.0，α=15°)Fig.6 The pressure distribution(Ma=1.0，α =15°)

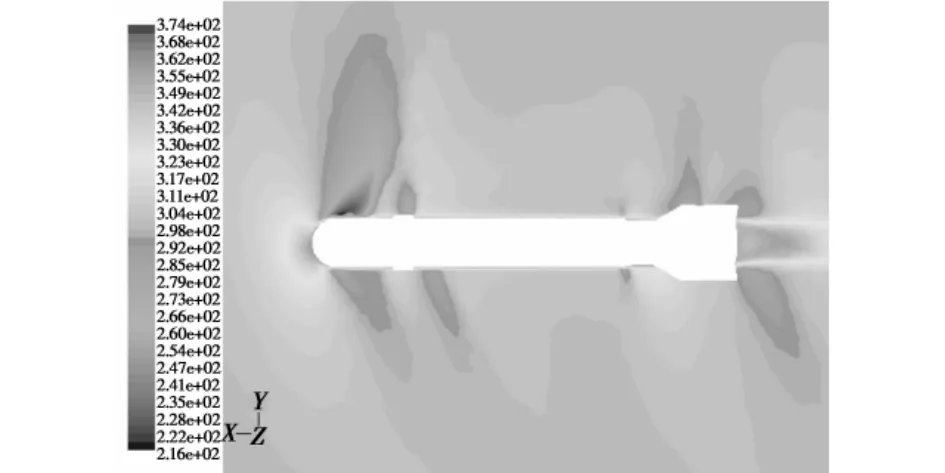
图7 温度分布图(Ma=1.0，α=15°)Fig.7 The temperature distribution(Ma=1.0，α =15°)

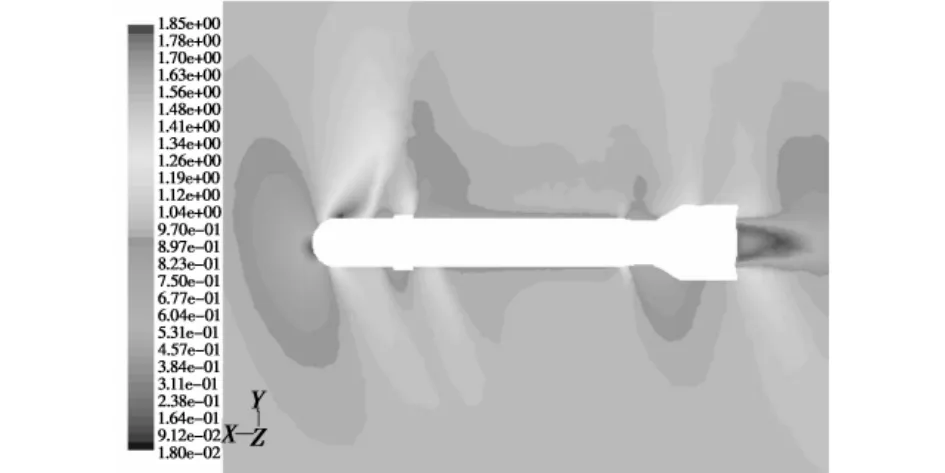
图8 马赫数分布图(Ma=1.0，α=15°)Fig.8 The mach number distribution(Ma=1.0，α =15°)

图9 静压分布图(Ma=1.2，α=0°)Fig.9 The pressure distribution(Ma=1.2，α =0°)

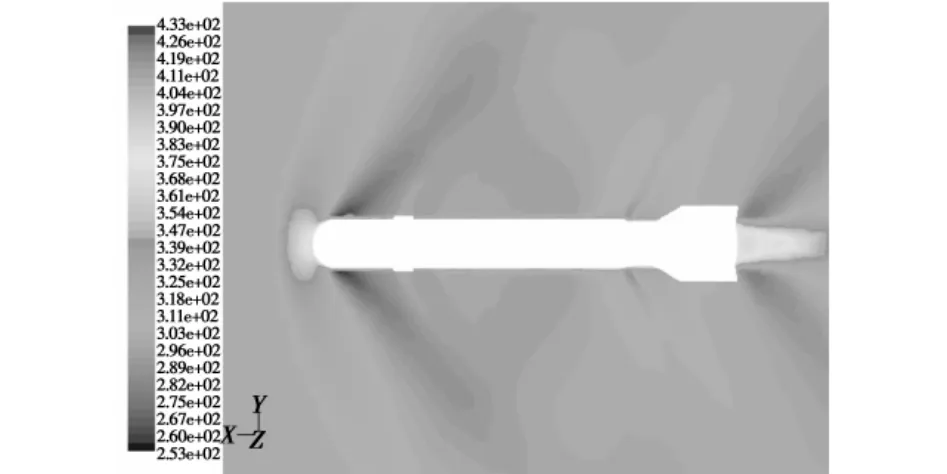
图10 温度分布图(Ma=1.2，α=0°)Fig.10 The temperature distribution(Ma=1.2，α =0°)

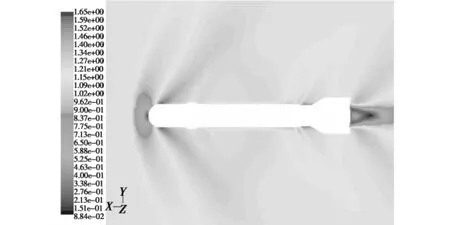
图11 马赫数分布图(Ma=1.2，α=0°)Fig.11 The mach number distribution(Ma=1.2，α =0°)

3.2 气动特性分析

通过大量三维绕流流场的数值模拟，得到炸弹在来流马赫数为0.7～1.4范围内(炸弹的有效工作段)的阻力系数与升力系数。其中，不同攻角条件下的阻力系数Cx与马赫数的关系如图12所示。可以看出，当攻角 α 为5°、10°或者15°时，升阻力系数 Cx变化趋势与零升阻力系数Cxo基本相同——来流马赫数Ma在0.7～1.1范围内，阻力系数随来流马赫数的增大而迅速增大;当来流Ma在1.1～1.4范围内，阻力系数基本保持不变。不同攻角条件下的升力系数Cy与马赫数的关系如图13所示。可以看出，升力系数Cy有如下变化趋势:在亚、跨音速阶段(Ma=0.7～1.1)，随着马赫数的增加，升力系数Cy基本保持缓慢增加;Ma在1.1～1.4范围内，升力系数Cy略有减小。

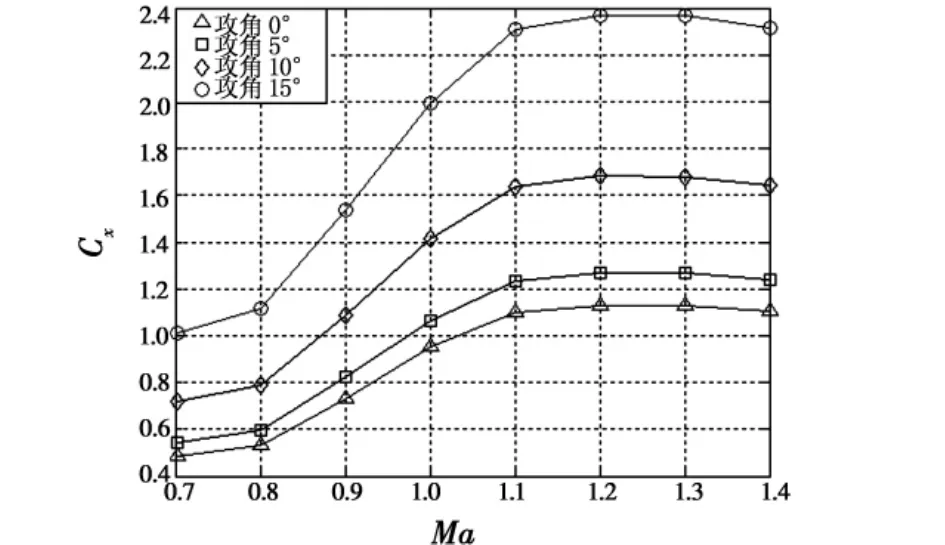
图12 阻力系数曲线Fig.12 The drag coefficient curve

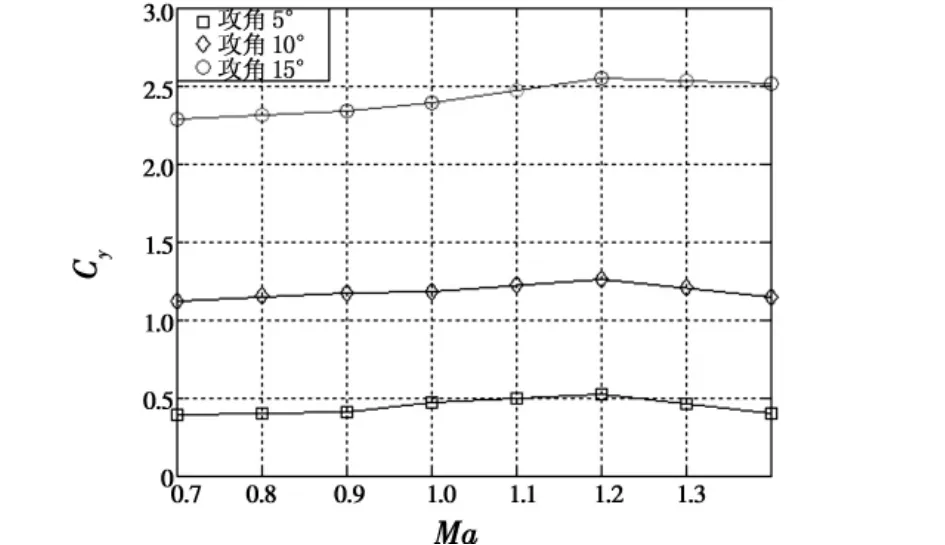
图13 升力系数曲线Fig.13 The lift coefficient curve

4 结论

本文应用计算流体力学软件Fluent 6.2进行数值模拟所得的仿真结果很好地展现了某型电视制导炸弹三维绕流流场的流动状态效果，得出了炸弹绕流流场宏观结构的变化规律和炸弹空气动力特性参数，本文给出的流场波谱为进一步等离子体激励改善该电视制导炸弹气动特性研究提供一定的参考与借鉴。

［1］朱自强，吴子牛，李津.应用计算流体力学［M］.北京:北京航空航天大学出版社，2001.

［2］王福军.计算流体动力学分析［M］.北京:清华大学出版社，2004.

［3］韩占忠，王敬，兰小平.流体工程仿真计算实例与应用［M］.北京:北京理工大学出版社，2004.

［4］ANDERSON J D Jr.Computational fluid dynamics:the basics with application［M］.Beijing:Tsinghua University Press，2002.

［5］张涵信，沈孟育.计算流体力学—差分方法的原理和应用［M］.北京:国防工业出版社，2003.

［6］恽起麟.风洞实验［M］.北京:国防工业出版社，2000.

［7］陈大伟，马小亮，杨国伟.超声速大攻角旋成体迎风激波数值模拟［J］.力学学报，2006(6):721-732.

［8］姜毅，郝继光，傅德彬.导弹发射过程三维非定常数值模拟［J］. 兵工学报，2008(8):911-915.

［9］雷娟棉，吴甲生.机载布撒器绕流场数值模拟［J］.弹道学报，2004(4):33-37.