用改进变异粒子算法实现突发威胁下的无人机航迹规划

刘 月，魏瑞轩，刘 敏，周 炜

(1.空军工程大学工程学院，西安 710038;2.中国人民解放军63650部队通信总站，新疆 马兰 841700)

0 引言

航迹规划是无人飞行器任务规划的重要组成部分，近年来各种优化算法在航迹规划中得到广泛的应用。Denton在动态规划理论的基础上提出的动态路径算法，但这种传统的算法计算较复杂，并且具有维数爆炸特性［1］。随着各种智能算法理论的日趋成熟，并被运用到航迹规划中，具有代表性的有模拟退火法、神经网络、遗传算法等［2－4］，这类智能算法相对于传统算法具有搜索速度快、精度高等特点。但是在涉及到突发威胁下的无人飞行器实时航迹规划时，这些智能算法也将不能保证全局最优解，并且可能会陷入维数灾难，使得计算时间过长，而不能用来解决实时航迹规划问题。本文通过研究改进PSO粒子群算法［5］，来解决突发威胁下的无人飞行器航迹规划问题。由于PSO算法的搜索过程中，随着粒子向发现的最优值位置聚集，粒子的速度逐渐下降，当速度下降到一定值时，粒子已失去活性，其运动趋于停滞，在时间性上无法满足实时航迹规划的要求，本文在此基础上提出自适应变异AMPSO算法，通过引入维量化活性度Ad的概念，当种群中所有粒子在某一维的搜索趋于停滞时，触发变异，变异措施的对象为全局粒子的位置和速度，有利于算法在该维上的充分搜索，提高搜索速度。

1 问题描述

航迹规划的实质是在一定的环境中，在特定的约束条件下，寻找一条从起始点到目标点满足某种性能指标的最优的或次优的飞行轨迹［6］。它的主要目的是根据飞行器性能和飞经的地形及敌情等信息规划出生存概率最大的飞行轨迹，从而保证飞行器在给定的时间内完成规定的任务。

具体地说，航迹规划系统要求得到的航迹能够有效避开敌方雷达的探测和敌方威胁的攻击;要求避开可能影响飞行的险要地形等。

突发威胁下的实时航迹规划还要求当临时出现事件未知，并可能会影响飞行的威胁场、恶劣气候等情况，或者已知的威胁、地形、气候等发生变化时，能够实时规划出新的飞行航迹［7］。

航迹规划需考虑诸多的约束条件，需要对大量的不同的信息进行处理，如规划区域内地形威胁、实时敌方威胁等，因此规划出满意的航迹实际上是一个多维多模多目标的优化问题。

2 PSO算法

本文针对上述问题采用了PSO算法，并针对该算法在解决实时航迹规划时存在的缺陷，提出具有变异机制的PSO改进算法。

2.1 PSO算法简介

PSO算法是设想仿真简单的社会系统——鸟群觅食过程的模型，研究并解释复杂的社会行为。与其他进化算法相似，PSO算法也是通过个体之间的协作与竞争，每个个体遵循一定的规则运动以实现复杂空间中最优解的搜索。由于其采用的是速度—位置搜索模型，因而算法简单，容易实现。

PSO算法首先生成初始种群，即在可行解空间中随机初始化一群粒子，每个粒子都代表了优化问题的一个潜在解，由3个指标来表征:位置、速度、适应度值。其中适应值(Fitness Value)由相应选定的目标函数确定。每个粒子将在解空间中运动，通常粒子将跟踪两个极值，一为粒子本身迄今找到的最优解Pbest，另一个为整个种群迄今找到的最优解Gbest，以此更新自身的速度和位置。通过计算粒子的适应度值衡量粒子的优劣程度，以优劣程度更新每个粒子的Pbest和种群的Gbest，如此逐代搜索。当迭代停止时，适应度函数最优的解变量即为优化搜索的最优解。

2.2 自适应变异AMPSO算法的变异时机

借鉴遗传算法GA的变异思想，在PSO算法通过引入维量化活性度Ad，当种群中所有粒子在某一维的搜索趋于停滞时，触发变异，从而提高PSO算法在搜索末期的活性。

维量化活性度Ad的定义如下:

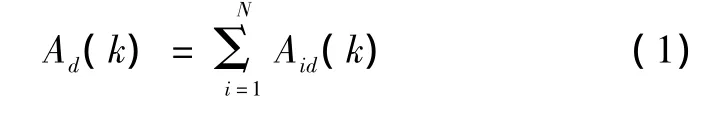
式(1)表示的是种群中所有粒子在第d维的量化活性度。

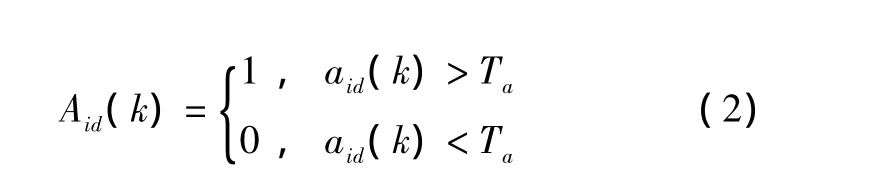
式中:Aid表示的是aid的0－1量化值。

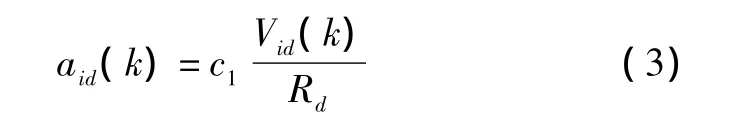
式中:Vid(k)为第k次迭代时第i个粒子在第d维上的速度;Rd为使用者控制的在第d维上的搜索空间范围，AMPSO中始终取为该维的空间长度(2Xmax);c1为可调参数，取值为1;aid(k)表示的是第k次迭代时第i个粒子在第d维上速度的活性度。

式中:Ta0为初始速度阈值，取值为0.001;K1为下降系数;NT为下降次数标记;Ta表示的是粒子在各维上的速度阈值。

当迭代中种群在某一维上的维量化活性度Ad(k)小于预先设定的阈值NA时，将自动下降各维上的速度阈值Ta(随NT的增大而减小)，同时标记维量化活性度超过范围的次数Nc，描述如下:

NT和Nc的初始值均为0，当Nc累计超过一定的次数K2时，触发AMPSO的变异，并在变异实施后，使Nc清零，重新计数。

2.3 AMPSO变异措施

AMPSO的变异措施是当Nc累计超过一定的次数K2时，从维量化活性度低于阈值NA的这Nc维中，随机抽取一维，对所有粒子在该维上的位置和速度实施重新初始化，使其获得新的空间位置和速度，描述如下:

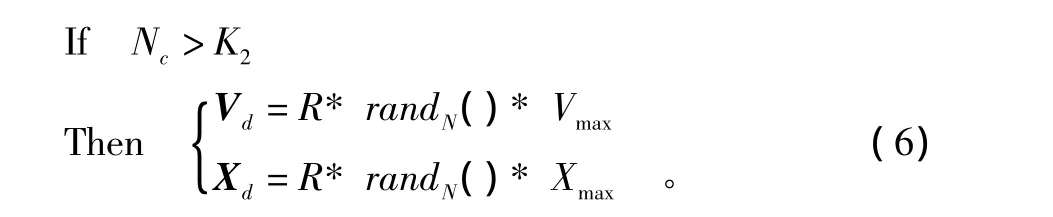
其中:randN()为N维向量，其中任一元素为［0，1］随机数;Vd=［V1d，V2d，…，VNd］，Xd=［X1d，X2d，…，XNd］，分别表示所有粒子在第d维上的速度和位置;N、Vmax、Xmax定义如前;R=(R1，R2，…，RN)，其中任一元素 Ri取值为

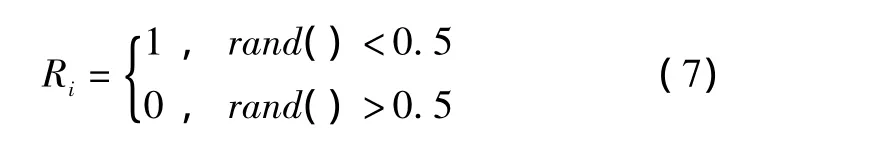
rand()为［0，1］随机数。

3 突发威胁下的航迹规划

假定飞行器上装有具有前视探测功能的威胁探测器(设探测距离d)以及能够实时处理的计算机，能及时探测到飞行器附近一定范围内的威胁信息，探测到新威胁信息后能及时地将其纳入新威胁图。规划方法是当未知威胁出现并纳入威胁图后，重新规划当前位置到目标点的新航迹。

3.1 航迹搜索空间构造(节点拓展法)

为了满足实时动态规划航迹的需要，采用由起点至目标点逐步拓展节点的搜索方式规划航迹，即从起点开始的每一次节点拓展，在现有的威胁图中，搜索满足航迹代价最小和步径要求的下一个节点。每次节点开始拓展搜索前，威胁探测器探测到的新威胁信息将和原有已知威胁一起被考虑到威胁计算之中，如此一步步的节点推进，直至到达目标点［8－9］。

3.2 威胁模型与航迹代价指标

1)威胁模型。

一个理论威胁突防模型由敷设在地形模型上的不同威胁模型、地形遮蔽算法和与RCS数据有关的飞行器特征模型组成。对于二维水平航迹规划而言，由于不考虑地形因素，故规划的主要目的是减少被敌方防空火力攻击、探测装置发现的概率。这里，以威胁的探测概率随距离增大指数递减为例进行仿真，形式如下:

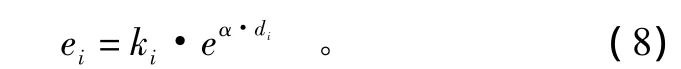
其中:ei表示第i个威胁源产生的威胁;ki为其对应的威胁幅值;α为威胁衰减系数;di为当前航迹上位置与第i个威胁源的距离，航迹上某一位置受到的总威胁为所有威胁源产生的威胁的叠加。突发威胁为预先未知的，飞行器只有在飞到其附近时方能探测到。

2)航迹代价指标。

对于采用节点逐步拓展的航迹规划，每一个待拓展节点希望其满足航路最短、威胁代价最小和步径长度的要求，为此设计评价粒子优劣的适应度函数如下:

其中:w1、w2、w3为权重;l为粒子位置到当前节点距离;Δl为步径长度;k为当前所有威胁的个数;L为粒子位置到目标点的距离;D为当前节点到目标点的距离。式中第1项和第3项为满足航迹最短和步径的要求，中间项为威胁代价。

3)航迹搜索空间的构造。

在文献［10］中采用一个有限项的一元多项式函数作为水平航迹的逼近，将规划问题简化为在一个一元函数多项式系数空间中的搜索寻优。由于多项式函数便于计算和求导，且系数有限，所以有利于算法收敛速度的提高。航迹可表示为

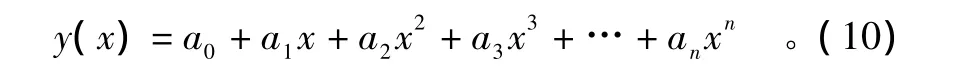
起点位置和期望的目标位置是已知的，分别设为(x0，y0)和(xt，yt)，则有:

其中:gi是 a3，a4，…，an的函数(i=1，2，3)，即系数a0，a1，a2可以由其他系数表示。于是最优航迹的规划问题变成了在缩小的多项式系数空间［a3，a4，…，an］的寻优。

需指出的是，采用如上的方式逼近航迹是有较大缺陷的，某些可能的航迹无法直接表示，例如图1所示的航迹。

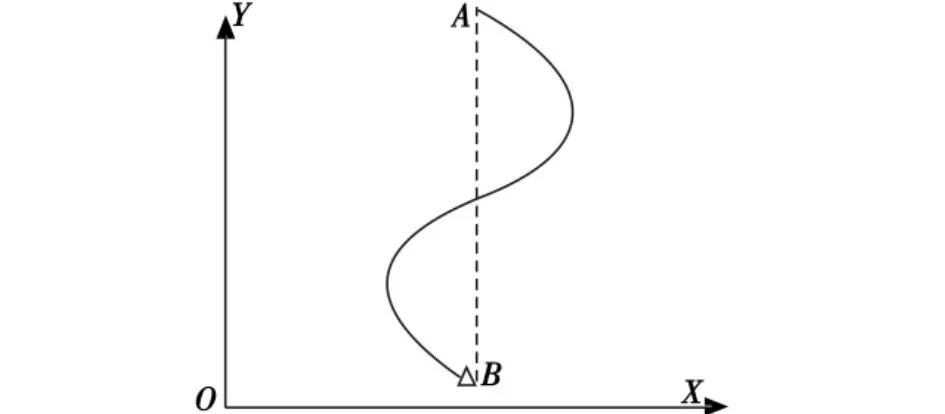
图1 航迹示意图Fig.1 Sketch map of flight path

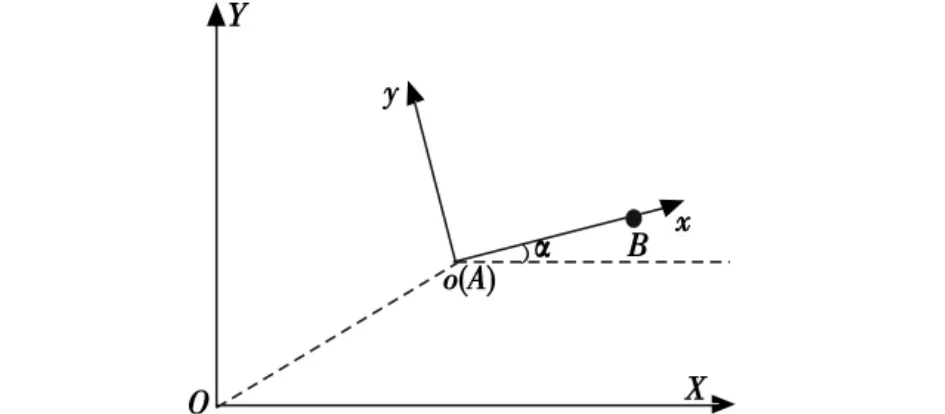
图2 新坐标系定义Fig.2 Definition of the new coordinate system

而如果以起点为坐标原点，以起点到目标点的方向为x轴，以其垂直方向为y轴，在很大程度上可以将航线看成是单值函数。新的坐标系定义如图2所示，此时，起点与目标点可以表示为(0，0)和(xt，0)。同样在考虑了起点、目标点约束和方位角约束下，可推导出新的变量关系表达式为

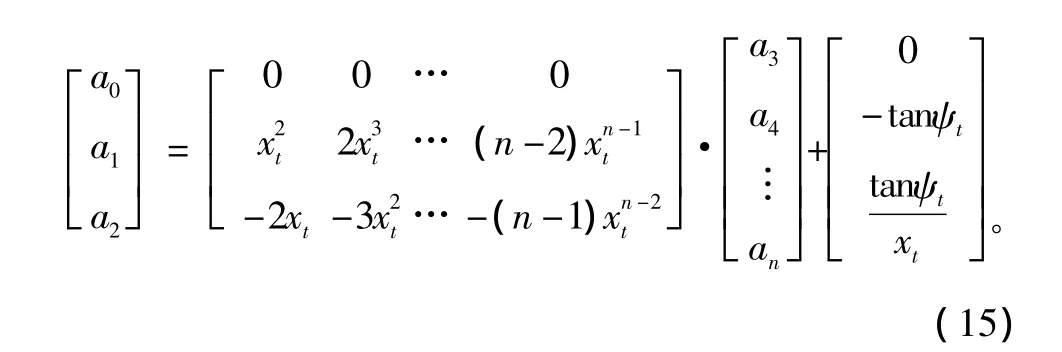
4)算法流程。

针对上述模型，具备了采用变异粒子群算法进行搜索的条件，设计其算法流程如下:

①每次节点拓展时，首先在搜索空间中随机地产生初始化规模为n的种群，种群中的每个粒子位置xi和速度 vi分别记为(xi1，xi2)和(vi1，vi2);

②利用适应度函数评价每个粒子优劣，并计算当前节点拓展时每个粒子的适应度值，当威胁探测器探测距离内出现未知威胁或已知威胁变化时，将其一起纳入威胁代价函数计算;

③记录和更新粒子的个体极值和全局极值;

④利用AMPSO算法含变异的位置与速度公式更新粒子的位置和速度;

⑤判断是否达到最大迭代次数，如果是，结束本次节点的拓展寻优，并将当前最优位置作为下一次搜索的开始节点，准备进入下次节点拓展;不是，则返回②。

4 仿真验证

仿真中，航迹搜索空间设置为100 km×100 km的区域，起始点和目标点分别设置在(10，10)和(90，90)，航迹代价中权重系数 w1、w2、w3分别设为 100、1、2，每次节点拓展时最大迭代次数为500，威胁的设置如表1所示。

表1 威胁参数设置Table 1 Parameter setting of the threats

其中:第5个威胁为预先未知威胁，威胁探测器探测距离设为20 km，每次步径长度取2 km，仿真结果如图3和图4所示，图中小圆点为每次拓展搜索得到的航迹节点。

实验在CPU 1.6 GHz的计算机上进行，软件环境为Matlab6.5，完成一次已知威胁下的全部规划约需130 s，其中节点拓展搜索约62～64次，如图3所示。于是，可计算出每次节点拓展搜索平均耗时约2 s。

在节点拓展搜索的第23次加入突发威胁(即在威胁的边缘)，通过仿真图4可以看出，航迹能有效地避开威胁，并能使航迹代价指标最小。仿真结果显示，完成一次含有突发威胁下的航迹规划约需136 s，其中节点拓展搜索约66～69次，平均耗时约2 s。

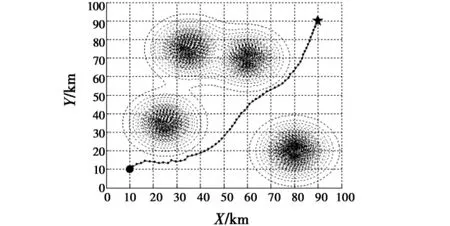
图3 已知威胁下航迹规划图Fig.3 Path planning without unexpected threats

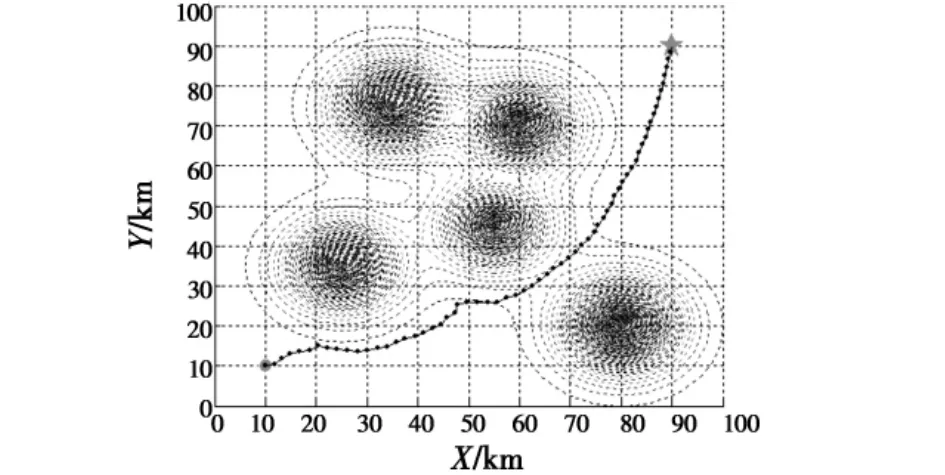
图4 存在未知威胁下航迹规划图Fig.4 Path planning with unexpected threats

假设飞行器速度为200～300 m/s，而规划中步径长度为2 km，即是说一次允许的实际规划时间为6.7～10 s。可见，利用AMPSO算法的节点拓展搜索的规划方法，可以满足应对突发威胁下航迹规划的要求，同时可以通过适当增大步径长度，减少每次规划时间，以降低对计算机性能的要求。

5 结论

本文将PSO算法成功应用于解决航迹规划问题，根据实际问题的需要提出了改进的AMPSO算法，对存在突发威胁情况下航迹规划问题进行了研究。仿真表明，基于AMPSO算法的航迹规划具有较快的搜索速度和较高的精度，对于不确定环境下的实时航迹规划，可以满足要求，不过本文所假设的威胁模型比较简单，不需要涉及到复杂的规划决策问题，这一点将在下一步工作中继续改进。

［1］DENTON R V，JONES J E，FROEBERG P L.A new technique for terrain following/terrain avoidance guidance command generation［R］.AGARD-CP-387，1985.

［2］任波，何可.改进遗传模拟退火算法的航迹规划方法研究［J］.飞行力学，2008，26(2):85-88.

［3］葛哲学，孙志强.神经网络理论与实现［M］.北京:电子工业出版社，2007.

［4］马云红，周德云.基于遗传算法的无人机航迹规划［J］.电光与控制，2005，12(5):24-27.

［5］KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Perth，Western Autralia:IEEE International Conference on Neural Networks，1995:1942-1948.

［6］闵昌万，袁建平.军用飞行器航迹规划综述［J］.飞行力学，1998，16(4):14-19.

［7］唐强，张翔伦，左玲.无人机航迹规划算法的初步研究［J］.航空计算技术，2003，33(1):125-128.

［8］HWANG J Y，KIM J S，LIM S S.A fast path planning by path graph optimization［J］.IEEE Transactions on System，Man，and Cybernetics，2003，33(1):121-128.

［9］HECKBERT P S，GARLAND M.Survey of polygonal surface simplification algorithms［Z］.SIGGRAPH’97 Course Notes，1997.

［10］唐强，王建元，朱志强.基于粒子群优化的三维突防航迹规划仿真研究［J］.系统仿真学报，2004，16(9):2033-2036.