动态贝叶斯网络在战场态势估计中的应用

赵晓辉，姚佩阳，张 鹏

(1.空军工程大学电讯工程学院，西安 710077;2.空军工程大学工程学院，西安 710038)

0 引言

战场态势估计是把来自多传感器和信息源的数据和信息加以联合、相关和组合，以获得精确的位置估计和身份估计，以及对战场情况和威胁及其重要程度进行实时的完整评价。由于战场信息复杂多变，具有高度的不确定性、不完备性，因此态势估计必须能对这种不确定性进行有效推理，并能对敌方下一步行动做出预测。

贝叶斯网络(Bayesian Network，BN)是一种进行不确定性推理和数据分析的有效工具，在战场态势估计中已经得到一定应用［1－2］。但是该方法未考虑连续时间因素，系统参数不能得到及时调整，有可能出现对未来态势的错误预测。而动态贝叶斯网络(Dynamic Bayesian Network，DBN)将BN扩展到对时间演化的过程进行表示，能够根据多个时刻的观测值对系统的各个时刻或某一时刻的状态进行估计和预测。

本文将DBN应用于战场态势估计，构建了包含连续变量的模型，并提出以卡尔曼滤波图模型法对连续隐状态DBN进行推理预测，有效解决了DBN的推理问题。通过实验仿真，证明了此方法的正确性。

1 贝叶斯网络

1.1 贝叶斯网络定义［3］

所谓的BN是指基于概率分析、图论的一种不确定性知识的表达和推理的模型。从直观上讲BN表现为一个赋值的复杂因果关系网络图，网络中的每一个节点表示一个变量，即一个事件，各变量之间的弧表示事件发生的直接因果关系。一个BN可以看成一个二元组 B=〈G，P〉，其中:网络结构 G，G=〈X，A〉是一个有向无环图(DAG)，其节点为随机变量 X={X1，X2，…，Xn}，n≥1，A是弧的集合。网络参数P，P中的每一个元素代表节点Xi的条件概率密度，由概率的链规则得:

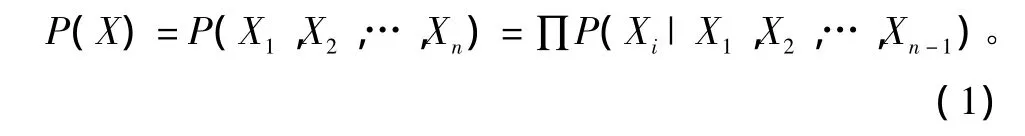
1.2 用于态势估计的贝叶斯网络模型

BN在态势估计上的应用已经有很多文献进行了研究［4］，下面以战争中一个简单场景为例，对BN的结构建模、参数学习和概率推理分别进行介绍。

假设我方直升机超低空飞行突袭敌方重要设施，欲对突袭的成功率进行估计。军事专家分析出影响成功率的态势因素为敌方部队组成、我方直升机情况、天气状况，详细包括:

1)环境因素，天气TQ(好、中、差);

2)敌方部队因素，攻击力GJ(强、弱)、侦察能力ZC(强、弱)，电子干扰强度DG(强、弱)，它们受敌方部队组成DZ和天气TQ影响;

3)我方部队因素，驾驶员技术等级JS(特级、一级)、抗干扰设备等级KG(一级、二级)，其中KG与DG决定双方干扰的结果GR(干扰成功、干扰失败)。

根据态势因素之间的因果关系确定BN的结构［5］，建立BN模型如图1所示。图1中圆形代表态势因素节点，其中 CG 为目标节点，DZ、TQ、KG、JS为输入节点，ZC、GJ、DG、GR 为过渡节点;有向线段代表节点间的因果关联。

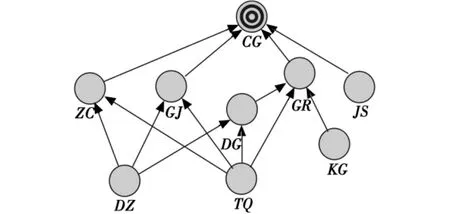
图1 贝叶斯网络模型Fig.1 Bayesian network model

确定各节点概率参数，方法主要有领域专家经验法、历史数据学习法，以及两者相结合的知识和数据融合法。经验法是指依靠领域专家，对节点直接给出影响概率分布，这种方法简单但是误差较大。学习法指利用大量观测数据，对节点概率进行估计，该方法较复杂但是在数据量大的情况下准确性高。融合法是指先用经验法进行估计，然后再用学习法提高精确度，其中领域专家的置信权值设定是关键。

为战场态势估计建立BN的主要目的就是利用观测数据对目标节点进行概率推理，将结果用于战场辅助决策。BN推理算法可分为精确算法(包括全局联合推理、图规约法、团树传播法、组合优化方法等)和近似算法(基于搜索的方法、仿真方法、变换方法、参数近似方法等)。使用BayesiaLab4.4工具自带的SPI算法对图1所示BN中成功率CG进行概率推理，推理结果:采用领域专家经验法自定义概率分布后进行的推理，得到CG=65.31%;在经验法基础上采用历史数据学习法对1000组数据学习后进行的推理，得到CG=78.33%;已知当前时刻所有输入节点取值情况下进行概率推理［6］，得到 CG=81.56%。

由于BN未考虑时间因素，无法对变量节点进行解释，如图1中TQ和DZ都是随着时间而变化的节点。而战场态势估计中的数据往往是时间序列数据，若能对其进行分析，不仅可以预测未来时间目标节点的概率取值，而且能对最大概率进行最优求解。这对战场态势估计的应用是非常重要的。

2 动态贝叶斯网络

在现代化战争中，战场态势瞬息万变，随着时间因素的引入，在不同时刻的状态所形成的数据，反映了所代表的变量的发展变化规律。要分析这种变化规律就必须建立相适应的动态模型。DBN将BN扩展到对时间演化的过程，反映变量的发展变化规律，可以用来解释动态的数据并对未来态势进行分析和预测。

2.1 动态贝叶斯网络定义［7］

为使DBN能够对复杂系统进行研究并建立相应的模型，首先需要做一些假设，即引入Markov假设和转移概率时不变假设。Markov假设是指每一时刻的状态变量集合只与前一个时刻状态变量的取值有关。转移概率时不变假设是指在一个有限的时间内条件概率变化过程对所有t是一致平稳的，不随时间的变化而变化。

DBN可定义为〈B0，B→〉，其中 B0表示最开始的BN，B→表示有两个以上时间片段的BN组成的图形。若用P(Xt|Xt－1)表示已知任一变量前一个时刻状态时，当前状态发生的概率表示第i个变量t时刻取值，Pa()表示其父节点;N表示变量数。DBN中任一节点的联合分布概率为

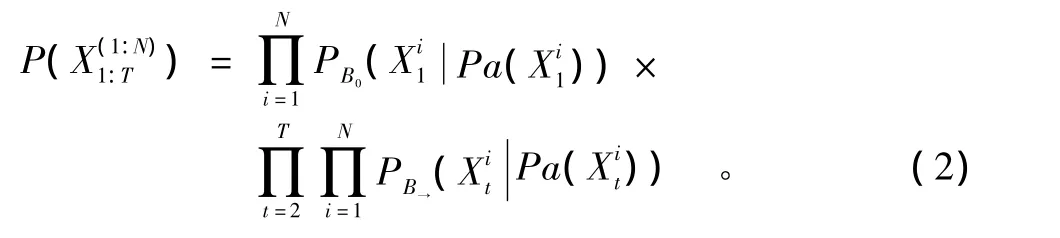
2.2 将BN转变为DBN

图1所示BN模型中，敌方部队组成DZ和天气TQ是不断变化的，为了能表示出这种变化，并能对未来的场景进行预测，将BN沿时间轴变化构建DBN，图2为DBN模型示意图。

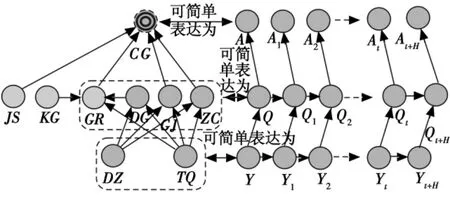
图2 动态贝叶斯网络模型Fig.2 Dynamic Bayesian network model

图2分为左右两部分。左半部为BN的结构，与图1类似;右半部中，Y表示变化的观测量，包括DZ和TQ两个变量节点;Q表示受Y影响的隐变量，包括ZC、GJ、DG、GR 4个与Y相关的过渡变量;A为目标变量，即成功率CG。

DBN对应的场景与BN相同，态势因素的确定方法也相同。但是DBN的结构需要表达出时间相关性，为了能够利用数据D中的时间信息，通过借鉴战争领域丰富的模型知识，将BN与卡尔曼滤波图模型(Kalman Filter Models，KFM)或隐马尔可夫模型(Hidden Markov Models，HMM)相结合，沿时间轴变化来构建DBN。其难点在于如何确定观测量Y与隐变量Q的相关性。

和BN相比，DBN的结构发生变换，其条件概率分布不可能像BN那样直接获得。首先要对数据D进行数据分析，得到BN的概率分布P，然后再根据D的时间序列获取观测量、隐变量相互关系，构建关系模型并学习得到影响参数r。最后将P与r代入DBN结构中，生成与时间t相关的条件概率分布函数。

利用DBN模型可以很好地表达随时间变化成功率CG的变化情况，可以根据大量观测数据推理变量可能取到的最大的值，对未来态势进行推测。它不仅具有静态BN的优势，如易于理解，建模快捷等，而且可以处理动态问题，大大扩展了使用范围。

对DBN进行推理，最容易理解的方法是将DBN展开成为BN，然后从时间的起点开始逐个片段地推算。但是在时间长片段多的情况下，该网络模型将会非常巨大，推算起来非常困难。文献［8］提出了用HMM模型解决DBN推理，然而图2中天气因素TQ为连续型随机变量，因此考虑用KFM进行推理。

3 KFM推理算法

对于隐变量连续的KFM，可以应用经典的LDS滤波或光滑算法进行学习和推理。对于所有随机变量的条件概率分布(Conditional Probability Distribution，CPD)都服从线性高斯分布的DBN，可以把它转化成KFM，用前向返回算法(Front Back，FB)对某一节点进行推理。用(xt|t，Vt|t)来分别定义P(Xt|y1:t)的均值和协方差，则前向算法可表示为

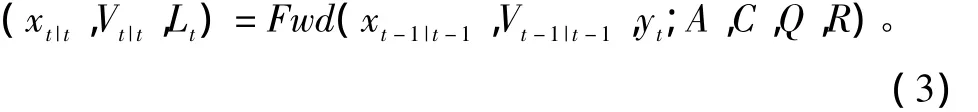
随后计算预计的误差及预测协方差矩阵、增益矩阵:

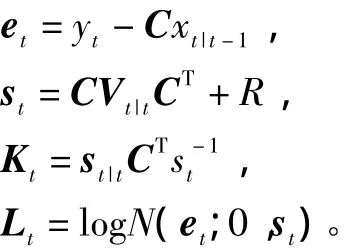
利用得到的数据更新估计数值的期望与协方差矩阵:

在光滑的基础上，较准确地估计出xt后，应用预测公式:xt+H|t=A(t，t+H)xt|t，可预测 xt+H的值，A(t，t+H)为t时刻到t+H时刻系统的转移矩阵。

4 仿真实验

为了验证图2所示DBN模型的正确性与有效性，采用Matlab7.0及贝叶斯网络工具BNT进行仿真验证。首先应用mk_KFM()函数建立与DBN对应的KFM网络，采用经典的LDS推理方式利用BayesiaLab生成的1000组数据进行学习，将各节点概率分布引入，最后应用FB算法对CG从时间上进行推理，得到20组CG的预测概率取值。推理结果和实际数据的误差比较见图3，其中横坐标为预测时间，纵坐标为平均相对误差。

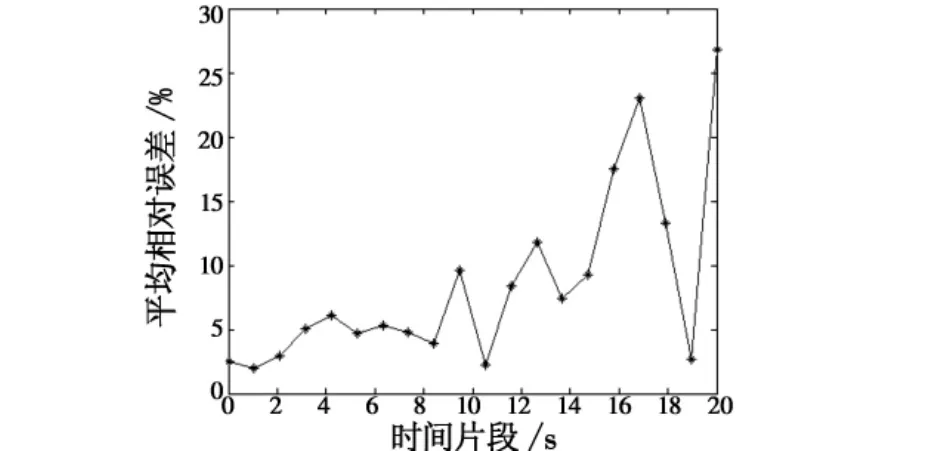
图3 不同时间片断的预测概率误差Fig.3 Prediction probability errors of different time fragments

由图3可知，在预测的初期误差较小，而后期误差逐渐增大，这是因为在预测时没有对新样本进行更新，得到的结果必然会随时间推移而出现大的偏移。因此采用KFM算法对DBN模型的推理预测可用于短时推理，通过仿真实验，说明了采用KFM算法的有效性，在DBN推理研究中具有很好的推广性。

5 结束语

本文针对战场态势估计中大量数据随时间变化的特点，通过构建动态贝叶斯网络模型，解决了变量节点的表达问题，分析了概率参数与推理的过程，并利用卡尔曼滤波模型法对推理进行仿真实验。仿真实验结果表明了所建立模型的有效性。在实际应用中根据变量的特性以及实时性的要求，可采用更快速的Boyen-Koller算法或者HMM算法。对于战场因素动态变化的问题，在研究军事问题中会经常遇到。动态贝叶斯网给出了建模和解决这类问题的数学方法，可以实时动态地处理影响分析和决策的种种因素，对指挥员的作战决策具有极大的参考价值。

［1］冀俊忠，刘椿年.贝叶斯网模型的学习、推理和应用［J］.计算机工程与应用，2003(5):24-27.

［2］王三民，王宝树.贝叶斯网络在战术态势评估中的应用［J］.系统工程与电子技术，2004(11):84-87，143.

［3］张连文，郭海鹏.贝叶斯网引论［M］.北京:科学出版社，2006:34-35.

［4］IVANSSON J.Situation assessment in a stochastic environment using Bayesian network［D］.Sweden:Linkoping University，2002.

［5］苏畅，宋亚兵，王力军，等.考虑天气因素的飞机作战效能对数模型［J］.电光与控制，2008，15(1):26-30.

［6］李伟生，王宝树.用于态势评估中因果推理的贝叶斯网络［J］.计算机科学，2002(11):50-52.

［7］PEARL J.Probabilistic reasoning in intelligent systems:networks of plausible inference［M］.San Francisco:Morgan Kaufmann，1988.

［8］樊红东，胡昌华，丁力.基于贝叶斯动态模型的某器件性能预测［J］.电光与控制，2006，13(1):70-72.

［9］肖秦琨，高蒿.动态贝叶斯网络推理学习理论及应用［M］.北京:国防工业出版社，2007，28-31.

［10］肖秦琨，高晓光.动态贝叶斯网络的无人机炮火校射［J］. 火力与指挥控制，2006，31(11):38-41.

［11］唐吉祥，沈云山.卡尔曼滤波器在炮位侦察雷达中的应用［J］.电光与控制，2004，11(1):48-49.