斜拉索风雨激振面内运动的非线性分析
李伟义,张琪昌,何学军
(天津大学机械工程学院,天津300072)
斜拉索风雨激振面内运动的非线性分析
李伟义,张琪昌,何学军
(天津大学机械工程学院,天津300072)
为深入研究斜拉索风雨激振面内的运动特性,依据弹性力学和气动弹性理论建立了连续斜拉索风雨激振面内非线性振动方程,利用伽辽金方法将偏微分方程转化为常微分方程.借助多尺度法得到面内一阶振动方程的平均方程和定常解,利用奇异性理论对系统进行分岔分析,确定了系统在零平衡点附近发生Hopf分岔对应的风速以及拉索发生风雨激振时对应的水线频率的范围.对拉索前四阶模态的振幅进行了数值模拟,考察了拉索以第一阶模态振动时风速、结构阻尼比等系统参数对拉索振幅的影响.研究表明,连续面内振动方程更能体现斜拉索风雨激振完整的动力学特性,同时系统中存在多种分岔行为.
风雨激振;非线性振动;水线;Galerkin方法;斜拉索
斜拉索作为主要受力构件广泛应用于大跨度桥.但由于拉索的大柔性、低阻尼及相对小的质量,在一定条件下极易发生由风雨导致的振动.风雨激振现象由Hikami等[1]首次发现,随后在许多国家和地区被观测到.拉索在一定雨量和风速范围内(约6~16 m/s)发生剧烈的大幅振动,会严重毁坏拉索.
斜拉索风雨激振已成为桥梁工程和风工程领域备受关注的问题.Wilde等[2]建立了拉索单自由度截段风雨激振模型,得到水线振幅与来流风速的关系.Peil等[3]通过试验研究,得出上水线的运动是导致风雨激振的主要原因.陈水生、赵跃宇等[4-5]研究了谐波激励作用下斜拉索的非线性动力学行为.禹见达等[6]进行了现场实测.李寿英等[7]依据风洞实验建立了连续体拉索风雨激振的理论模型,采用数值方法对偏微分方程直接进行求解和分析.
上述研究为本文建立和完善斜拉索风雨激振连续体模型并进行理论分析提供了很好的借鉴.笔者建立和完善了连续斜拉索风雨激振的面内振动方程,对拉索的面内运动进行了非线性分析,由分岔方程开展了系统的分岔研究,应用奇异性理论得到转迁集,画出平衡点附近的分岔图.利用数值模拟对理论分析的结果进行了验证;同时研究了系统参数对拉索振幅的影响,并给出了实际工程解决方案.

图2 拉索单元受力分析Fig.2 Force analysis of the cable element
1 建立系统力学模型
考虑几何非线性和拉索垂度是建立斜拉索连续体模型的前提.鉴于问题的复杂性,做出如下假定:
(1)准定常假设成立;
(2)不考虑拉索抗弯、抗扭及抗剪刚度的影响;
(3)拉索的变形本构关系服从虎克定律且各点受力均匀;
(4)不计拉索的重力对拉索弦向张拉力的影响[4].
建立如图1所示的Oxyz坐标系,斜拉索在x-y面内的振动称为面内振动,在x-z面内的振动称为面外振动.索的长度为l,两端点垂直及水平方向的距离分别为L′和L,拉索与水平方向的倾角为α.
截取一微段斜拉索[8],如图2所示.图2中,T为静态下拉索沿切向的张力;M为拉索单位长度的质量;s为索的弧长坐标;ds为索单元在静态下的长度;u、v、w分别为索单元在x、y、z轴偏离静平衡位置的位移,是x和t的函数;ds′为索单元发生变形后的长度;t′为振动过程中切向的张力相对于初始张力的变化量.设c1、c2、c3分别为拉索沿x、y、z轴上单位长度的线性阻尼系数;fx、fy、fz分别为拉索在x、y、z轴上单位长度所受的气动力.索单元沿y轴的静平衡方程为


图1 考虑垂度的空间拉索示意Fig.1 Cable with small sag in space
静态情况下,考虑拉索的小垂度,做出近似

将式(2)代入式(1)进行积分,得到拉索在静态下的垂度曲线
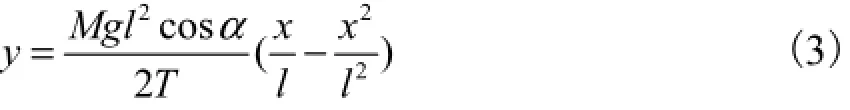
如不考虑轴向振动和面外振动,由牛顿第二定律建立系统的动力学方程
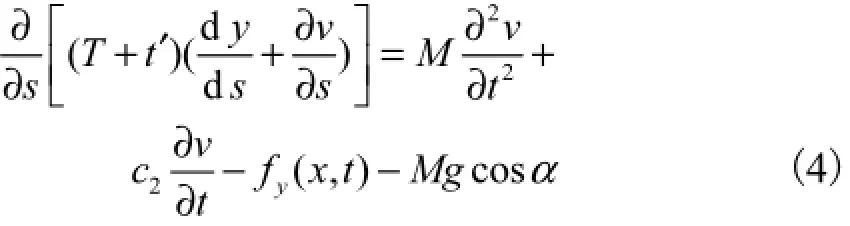
由公式[8]

将式(4)化简为

式中:H′是静态下拉索沿x轴的张力;h是振动过程中沿x轴的张力相对于初始张力的变化量,


式中系数im(i=1,2,…,5)为积分常数.
2 水线的运动规律
研究表明,上水线在临界位置附近的微小变化引起拉索气动力的剧烈变化[9],下水线对系统影响很小.因此忽略下水线,只考虑上水线对拉索振动的影响.假设水线为正弦振动且在运动过程中外形和大小保持不变,即
式中:ω是水线的振动频率;am是水线的振幅,度.am与来流风速的关系式[2]为

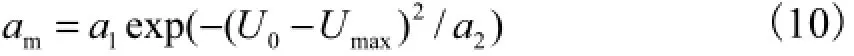
式中:1a、2a、maxU是与给定拉索有关的常数[7];0U为来流风速.
如图3所示,在来流风速U0作用下,拉索倾角α=30°,风向角β=35°,该姿态最易发生风振[10].如图4所示,Urel为拉索与来流的相对风速,与z轴的夹角为φ;U为U0在垂直于拉索所在振动平面的分量,与z轴的夹角为γ;水线在平衡位置附近的振动角度为θ,顺时针方向为正;θ0为水线在拉索表面的平衡位置角.当α=30°、β=35°时θ0的表达式[10]为

拉索气动力的表达式为


图3 拉索姿态Fig.3 Attitude of the cable

图4 拉索、水线与风速的关系Fig.4 Relationship among the cable,the rivulet and wind velocity
其中
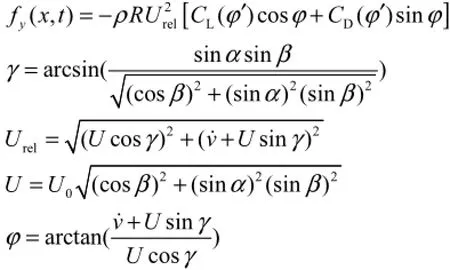
式中:ρ为空气密度;R为拉索半径;LC、DC分别表示带水线拉索30α=°、35β=°的平均升力和阻力系数[7].
3 求解系统平均方程
拉索主要的振动是面内振动.选取参数[6]l=, 121.91,m,拉索预紧力H0=3.15×106,N,M=,51.8,kg/ m,ξ=0.001,R=0.059,5,m,ρ=1.29,kg/m3,EA=,21.132× 108N,U0=12 m/s,式(10)经高阶泰勒展开得到
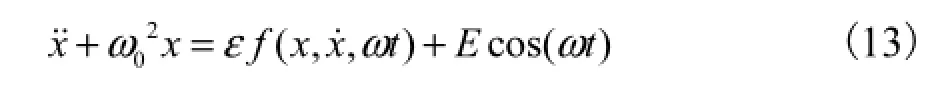
式中0ω是拉索的一阶固有频率.通过计算发现零点为系统的非双曲平衡点,并且系统满足Hopf分岔定理[11]的条件,因此系统在平衡点附近发生Hopf分岔.当0U<4.02 m/s时,平衡点是渐进稳定的焦点;当0U=4.02 m/s时,平衡点是中心;0U>4.02 m/s时,平衡点是不稳定的焦点,在其附近出现一渐近稳定的极限环.
利用多尺度法[11]对式(13)进行求解,令

式(13)的解可写成

通过计算得到平均方程

式中:1b、2b及1d是方程(13)中部分非线性项的系数;系统发生自激振动得拉索发生自激振动对应的水线频率为ω>6.463,58,rad/s或ω>6.410,37,rad/s,此时ω0=6.436,92,rad/s,在上述水线频率范围内取不偏离0ω很远的值6.41,rad/s和6.463,9,rad/s,定常解a分别为0.122,m和0.110,8,m.
4 进行局部分岔分析


显然detA(0,0,0,0)≠0,所以G( a,μ,α, β)是g( a,μ)的普适开折,余维数为2.应用奇异性理论进行持久性分析,得出分岔点集B;滞后点集H={(α, β)∈R2α=β3/27};双极限点集D=∅(空集);转迁集Σ=B∪H∪D.如图5(a)所示,转迁集将平面α-β划分为4个连通的分支;图5(b)为G( a,μ ,α, β)在不同(α, β)数值下的静态分岔图.
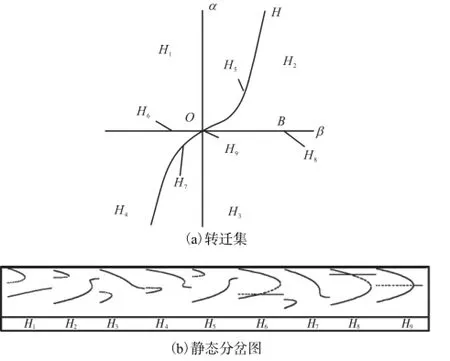
图5 普适开折分岔图Fig.5 Bifurcation diagram of universal unfolding
HH是系统在不同的开折参数下所有可能的解曲线,实线是系统的稳定解,而虚线是不稳定解.通过对局部分岔行为的初步研究,表明斜拉索风雨激振系统中存在多种分岔行为.对于原系统参数与开折参数之间的关系以及如何通过分岔研究对系统进行参数控制,还有待于进一步深入研究.
19~
5 数值分析
多阶模态的参与及高阶模态的伴随使拉索风雨激振问题异常复杂.因此在实际研究中往往忽略高阶模态,取以拉索发生单模态振动为例,以第一阶模态发生振动时,振幅值与解析解吻合;以第三阶模态发生振动的振幅远小于第一阶模态的幅值;第二或第四阶模态时,拉索发生很微小的振动.这主要是假设水线在全部拉索上形成,对称的荷载不会引起对称振型的振动所致.拉索以第一和第三阶模态发生风雨振的相图如图6和图7所示,振动为稳态运动,收敛于稳定的极限环.由于篇幅的限制,不再给出第二、四阶模态的相图.

图6 第一阶模态拉索相图Fig.6 Phase portrait of the first order mode of cable
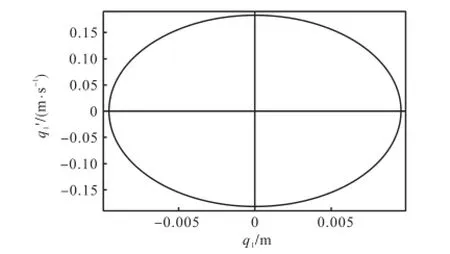
图7 第三阶模态拉索相图Fig.7 Phase portrait of the third order mode of cable
拉索以第一阶模态发生风雨振时,系统主要参数与拉索振幅的关系曲线如图8和图9所示.

图8 来流风速与面内最大振幅的关系Fig.8 Relationship between wind velocity and the maximum amplitude
如图8所示,拉索发生风雨振的起振风速为6 m/s,拉索振幅最大时的风速为12 m/s.如图9所示,阻尼比ξ体现了结构阻尼对结构振动的抑制程度,拉索的振幅随阻尼比的增大迅速减小.无外加阻尼器时拉索的结构阻尼很弱,ξ越大表示外加阻尼越大.这一特性对实际工程显得尤为重要.实际工程中通过在固定端安装阻尼器增大系统的结构阻尼以减小振动,或者通过在拉索间连接辅助索从而减小索的有效长度、提高索的固有频率达到抑振的目的.
6 结 论
(1)本文对已有理论模型做出改进:将拉索的轴向与坐标轴重合,这样减少一个方程的同时能更方便、快捷地进行理论分析;考虑了拉索振动过程中张力的变化量中非线性项的影响.
(2)验证了系统在零平衡点附近发生Hopf分岔,并确定了系统发生Hopf分岔时对应的风速;确定了拉索发生风雨振时对应的水线频率的范围.证明斜拉索风雨激振系统中存在多种分岔行为.
(3)针对拉索前4阶模态振动的振幅进行了数值模拟,验证了面内拉索一阶模态振动的振幅的解析解,并研究了系统参数对拉索振幅的影响,提出了相应的解决方案,对实际工程问题有一定的借鉴价值.
[1] Hikami Y,Shiraishi N. Rain-wind induced vibrations of cables in cable stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics,1988,29:409-418.
[2] Wilde K,Witkowski W. Simple model of rain-wind induced vibrations of stayed cables [J]. Journal of Wind Engineering and Industrial Aerodynamics,2003,91:873-891.
[3] Peil U,Nahrath N. Modeling of rain-wind induced vibration[J]. Wind and Structures,2003,6(1):41-52.
[4] 陈水生,孙炳楠. 斜拉桥拉索模态耦合非线性共振响应特性[J]. 工程力学,2003,20(1):137-143. Chen Shuisheng,Sun Bingnan. Nonlinear internal resonance characteristics of modal interaction for stay cables of cable-stayed bridges[J]. Engineering Mechanics,2003,20(1):137-143(in Chinese).
[5] 赵跃宇,王连华,陈德良,等. 斜拉索面内振动和面外摆振的耦合分析[J]. 土木工程学报,2003,36(4):65-69. Zhao Yueyu,Wang Lianhua,Chen Deliang,et al. Coupled analysis of out-of-plane oscillation and in-plane vibration for stay cable[J]. China Civil Engineering Journal,2003,36(4):65-69(in Chinese).
[6] 禹见达,陈政清,王修勇,等. 基于现场观测的拉索风雨振特性研究[J]. 湖南科技大学学报:自然科学版,2006,21(2):22-24,47. Yu Jianda,Chen Zhengqing,Wang Xiuyong,et al. Study on characterization of rain-wind induced stay-cable vibrations from field measurements[J]. Journal of Hunan University of Science & Technology:Natural Science Edition,2006,21(2):22-24,47(in Chinese).
[7] 李寿英,顾 明,陈政清. 准运动水线三维连续弹性拉索风雨激振理论模型[J]. 工程力学,2007,24(6):7-14. Li Shouying,Gu Ming,Chen Zhengqing. Analytical model for rain-wind-induced vibration of three-dimensional continuous stay cable with quasi-moving rivulet[J]. Engineering Mechanics,2007,24(6):7-14(in Chinese).
[8] Irvine H M. Cable Structure[M]. Cambridge,Massachusetts:The MIT Press,1981.
[9] Gu Ming,Lu Qian. Theoretical analysis of wind-rain induced vibration of cables of cable-stayed bridges[J]. Journal of Wind Engineering,2001,89:125-128.
[10] Gu Ming,Du Xiaoqin. Experimental investigation of rainwind-induced vibration of cables in cable-stayed bridges and its mitigation [J]. Journal of Wind Engineering and Industrial Aerodynamics,2005,93:79-95.
[11] 王洪礼,张琪昌,郭树起,等. 非线性动力学理论及应用[M]. 天津:天津科学技术出版社,2002. Wang Hongli,Zhang Qichang,Guo Shuqi,et al. Theory and Application of Nonlinear Dynamics[M]. Tianjin:Tianjin Science and Technology Press,2002(in Chinese).
Nonlinear Analysis of In-Plane Motion of Rain-Wind-Induced Vibration of Stay Cable
LI Wei-yi,ZHANG Qi-chang,HE Xue-jun
(School of Mechanical Engineering,Tianjin University,Tianjin 300072,China)
For in-depth study of the characteristics of in-plane motion of rain-wind-induced vibration of the stay cable,the nonlinear equation of the in-plane vibration of continuous stay cable has been presented on the basis of elastic mechanics theory and aeroelasticity theory. The partial differential equation has been diverted into ordinary differential equation with Galerkin method. The averaged equation and the steady state solution have been obtained with the method of multiple scales and bifurcation analysis has been conducted with singularity theory,which determines the wind speed as Hopf bifurcation occurs at the origin point and the range of rivulet frequency when the rain-wind-induced vibration of stay cable happens. The vibration amplitudes of the first four order modes have been numerically simulated to study the impact of system parameters,such as the wind speed and the cable damping ratio on the vibration amplitude while the stay cable is vibrating in the first order mode. Study results show that the nonlinear equation can reflect the dynamic characteristics of the in-plane motion of rain-wind-induced vibration of stay cable better,and various bifurcation behaviors exist in the system.
rain-wind-induced vibration;nonlinear vibration;rivulet;Galerkin method;stay cable
O322
A
0493-2137(2010)02-0156-05
2008-12-12;
2009-04-16.
国家自然科学基金资助项目(10872141);教育部博士点基金资助项目(20060056005).
李伟义(1981— ),女,博士,liweiyi@tju.edu.cn.
张琪昌,qzhang@tju.edu.cn.

