随动系统数字化

李 娜

(国营第七八五厂，山西太原030024)

0 引言

随动系统按指控系统送来的目标信息，在高低角和方位角两个通道，完成对未来目标的跟踪、对准，直至发射。所以，随动系统的对准、跟踪精度和响应快慢直接影响作战效果。

微处理器使得随动系统电脑化，软件决定了控制装置的功能。现代伺服系统回路的反馈部分，基于“IF…THEN…”软件规则的动态变化形成数字式反馈补偿。随动系统应具备快速性好，无超调，无静差特点。工程上为了达到这些技术指标同时又要考虑实际工作中算法简单有效，对此本文采取数字式模糊/PID混合控制方法来解决。

1 伺服系统功率放大器

随着晶闸管技术的发展，产生了能满足各种性能要求的晶闸管直流调速系统。在晶闸管供电的直流调速系统中，由于晶闸管元件的单向导电性，必须在电动机回路中采取适当措施，才能实现电动机的可逆运行。通过改变电枢电压极性实现可逆运行的系统称为电枢可逆系统，如图1所示。

图1 电枢可逆系统

两组晶闸管之间是由一个交流电源同时向两组晶闸管供电成为反并联线路。如果两组都工作在整流状态，则会在两组晶闸管之间产生很大的直流环电流。这实质上是电源两端直接短路，会使设备损坏，是绝对不允许的。通常采用的抑制脉动环流的办法是在环流回路中串入环流电抗器L1、L2、L3和L4。环流电抗器必须在整流状态侧和逆变状态侧各设置两个，因为处于整流状态侧的晶闸管除流过脉动电流外，还流过电动机负载电流，使环流电抗器饱和，不能起限流作用，所以必须依靠逆变状态晶闸管一侧的环流电抗器来限制脉动环流。

2 计算机控制的随动系统

2.1 数字式的直流电力传动系统

计算机控制直流传动系统由计算机控制器、驱动电路、电流和速度反馈电路、功率放大电路、位置传感器和直流电动机组成，如图2所示。

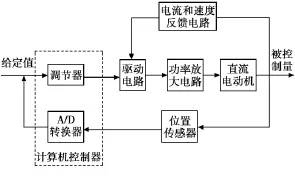
图2 计算机控制直流传动系统结构

计算机控制器采用了单片机80C196KC，其单片机本身具备D/A转换功能，通过脉冲宽度调制寄存器实现的。其模拟量的表现形式为宽度可变的脉冲波，亦称PWM。当该寄存器出现于窗口0时，可对其进行写操作，写入数据后，PWM的宽度随之而定。因为该寄存器的内容只能在00H～0FFH之间变化，所以PWM的可调节范围是一定的。

本系统设计采用80C196KC单片机，其为晶振10 MHz。PWM脉宽频率由IOC3输入输出控制寄存器在窗口为1，设置由第2或3位来决定，本系统采用 PWM输出的频率9.8 kHz，周期约为102 ms。PWM的占空比取决于PWM寄存器的值，其分辩率为1/256。

2.2 数字电力传动系统位置反馈信号的采样

电动机位置的被控制量是模拟量形式的物理量，通过旋转变压器和A/D转换将模拟量转换为数字量进行角度计算。旋转变压器粗示角度a正弦波的个数与精示角度b正弦波的个数比为1∶20，亦是1个粗示正弦波里套着20个精示角度正弦波。

因为粗示角度a正弦波的个数与精示角度b正弦波的个数比为1∶20，所以1个精示角度b对应于粗示角度a的范围是0°～ 18°(360°/20=18°)。实际角度 γ的计算公式:

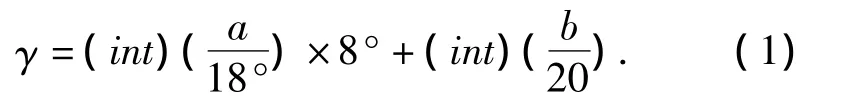
2.3 计算机控制系统中的数字运算方法

2.3.1数字式PID调节器

在连续控制电力传动系统中，PID控制器得到广泛的应用。在计算机控制系统中，PID调节可用软件实现。PID调节器对电动机的位置进行控制，调节器的输入量是输出量y(t)与给定值r(t)的误差e(t)，

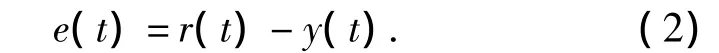
在工程实际应用中，采用了PID调节器，其时域的表示形式为

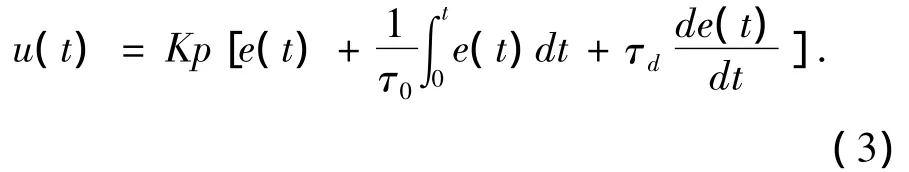
式中:Kp为比例放大系数;τ0为积分时间常数;τd为微分时间常数。

在数字计算机中用软件来实现PID控制，可以使用数字逼近的方法。用求和代替积分，用差商代替微分，使PID算法离散化。

PI调节器将比例与积分组合即可

PI调节器在计算中需要将系统运行以来的误差值e(0)…e(k)全部计算。PID调节器是比例、积分、微分调节器的组合，可以得到

其中，Kp为比例环节:成比例的响应控制系统地偏差e(k)，偏差一旦产生，控制器立即产生控制作用，减少偏差;KI为积分环节:主要消除静差，提高系统的误差度;KD为微分环节:响应偏差信号的变化趋势(变化速率)，并能在偏差信号变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减少调节时间。

计算机在PID的每一步运算中，需要存储PID调节器前次的输出值u(k－1)和前次的误差值e(k－1)。

2.3.2数字PID调节器的饱和抑制法(积分分离法)

在闭环控制系统中，由于执行机构的线性范围有限，当控制量U(k)对应于执行机构的线性范围以内时，随控制量U(t)的增大，执行机构的输出功率也增大，反之减小。但是当U(k)增大到执行机构的输出功率最大(电机转速最高)以后，U(k)增加功率也不会再增大，此时控制量为Umax。这种饱和现象使执行机构不能及时按U的要求动作，产生较大偏差，使超调量增大甚至振荡。因此，PID调节器需要设计为限幅调节器，限幅调节器就是PID调节器输出U(k)的值为:Umin≤U(k)≤Umax。

在系统中如果PID控制器计算得到的是U(k)≤Umin或者U(k)>Umax，而强制使输出是Umin或者Umax，则控制不能达到预期的结果，甚至引起系统的振荡。

计算机控制的系统中，使用积分分离法。积分分离法的设计思想是:在误差e(k)较大时，调节器不进行积分运算，只计算比例项和微分项;当误差e(k)小到进入误差带时，才进入积分运算。这样一开始误差e(k)很大，积分不累加，防止了积分项过大。进入误差带后，才开始累加积分增量ΔIk，有利于消除偏差。而且偏差小时，积分累加之和也小，即使饱和也容易退出。于是积分分离法的PID的算法为

其中，B为系统本拍的误差宽度;ΔIk为系统本拍PI控制器的积分增量。

当系统误差－B≤e(k)≤B时，PI控制器的积分增量ΔIk累加;若系统误差在宽度B的误差带外，积分项的增量不累加。

3 模糊逻辑控制器设计

计算机软件实现的模糊控制器是控制系统的中心，由三部分组成“模糊化”，“模糊控制规则”和“模糊判决”。这种控制方法是非线性的控制方法，适应于解决非线性问题，对无法取得数学模型或数学模型相当粗糙系统可以取得较满意的控制效果。

系统中的偏差E，偏差的变化率Ec和模糊控制器的输出控制量U都是确定的数值。把E，Ec的精确量转换成控制规则所需的模糊量，即找到该精确量隶属于某个模糊子集的隶属度。如图3所示。本文选择位置误差E和位置误差变化Ec作为控制器的输入量，由电压值U作为控制器输出。

图3 双输入单输出控制系统

用梯形隶属函数可以避免大量的运算，大大减少模糊化时的计算工作量，有利于用软件实现模糊化和实时控制。不同的隶属函数对系统有不同的响应，当遇到偏差较大时，采用高分辩率的模糊集，它引起的输出变化相对强烈，控制的灵敏度高;当遇到偏差很小或接近零时，则应用低分辩率的模糊集，它引起的输出变化相对缓慢，控制特性较为平缓，系统较稳定。

定义变量的变化范围通常七个模糊集:

模糊变量 E 模糊集为:E={NB，NM，NS，ZO，PS，PM，PB}

模糊变量 Ec模糊集为:Ec={NB，NM，NS，ZO，PS，PM，PB}

模糊变量 U 模糊集为:U={NB，NM，NS，ZO，PS，PM，PB}

对每个变量用模糊集来描述，NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)量化为7级。模糊集所代表的语言值表示人对输入变量和输出变量大小的反映。

输入模糊化后，应进行模糊推理，模糊推理采用条件语句“IF…THEN…”。本系统的模糊控制器是双输入单输出形式，采用模糊推理形式:

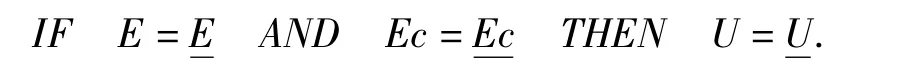
式中E是系统偏差，使系统给定量与反馈量之差的模糊子集。Ec是系统偏差E的变化率的模糊子集。

可以根据系统误差量E及误差量变化Ec的相互关系归纳出控制规则:

(1)误差量很大时:误差量变化与误差量方向一致，则系统的误差量有增大的趋势。此时，控制量应取最大值，使误差尽快减小。

(2)误差量很大时:误差量变化与误差量方向相反，则系统的误差量有减小的趋势。此时，为了使尽快减小误差量，同时避免出现超调控制量应取较大值。

(3)误差量较小时:根据误差量变化情况，控制量可适当取一些较小值。

模糊控制器的控制规则，可根据系统误差及误差变化得模糊控制规则49条。以下是部分规则:

4 结论

随动系统数字化后，在阶跃信号给定下，可以达到缩短调节时间，降低最大超调量和减少超调次数。使随动系统有良好的静态特性，较高的调节精度，比较理想的动态过渡过程。

图4 模糊控制器程序框图

原随动系统的技术指标要求:

消除150密位失调角:响应时间≤3秒、振荡次数≤6次;

随动系统数字化后能达到的技术指标:

消除150密位失调角:响应时间≤3秒、振荡次数≤4次;

记录图形如图5:横轴每50单位表示1秒，纵轴表示失调角密位。

图5 消除方位150密位失调角的时间振荡次数

［1］黄坚.自动控制原理及其应用［M］.高等教育出版社，2004.1.

［2］刘复华.8XC196KX单片机及其应用系统设计［M］.清华大学出版社，2002.7.

［3］曾光奇.模糊控制理论与工程应用［M］.华东科技大出版社，2006.8.