数字滤波在某温控报警装置的应用探讨

金魁生

(国营第七八五厂，山西太原030024)

0 引言

在实际的测量过程中，被测信号中不可避免地会混入一些干扰和噪声。为了抑制和消除这些干扰和噪声，可以采用硬件抗干扰的方法，如屏蔽或滤波器;也可以用软件处理的方法，即数字滤波。硬件或软件的方法几乎可以达到相同的功效，毫无疑问，软件处理方法更灵活，更经济。

1 基本数字滤波算法

限幅滤波;算术平均值滤波;中位值滤波;低通数字滤波。下面逐一介绍。

1.1 限幅滤波

限幅滤波又叫程序判断滤波。滤波原理是根据经验判断两次采样值之间的最大偏差δA。

如果本次采样值 An与上次有效值 An－1之差│An－An－1│≤δA，则本次采样值有效;

如果本次采样值 An与上次有效值 An－1之差│An－An－1│>δA，则本次采样值无效，以上次有效值作为本次有效值。

当δA=5时的限幅滤波效果图，如图1所示。

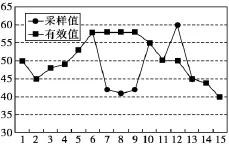
图1 限幅滤波效果图

由效果图可见，限幅滤波能有效抑制因偶然因素引起的较大的脉冲干扰，而对周期性的干扰却无能为力。

1.2 算术平均滤波

算术平均滤波，即连续采样N次，并对N次采样值进行算术平均运算，运算结果作为有效值。

算术平均值法对受到随机干扰的信号很有效，但对脉冲性干扰的抑制作用较差。N值较大时，信号平滑度高，但灵敏度降低。实际应用中，为了提高速度，程序常用移位来代替除法，则N常取2的整数次幂［2］。

1.3 中位值滤波

所谓中值滤波是对某被测参数连续N(一般N取奇数)次采样，然后对采样值按大小排序，取中间值作为本次有效值。中值滤波对消除偶然因素引起的波动干扰比较有效，且N愈大滤波效果愈好。对温度、液位等变化缓慢的被测参数采用此方法能受到良好的滤波效果;但对力、速度等变化快的参数不宜采用中值滤波。N的取值视具体情况而定，一般取3或5，对于变化很慢的对象可适当增加N值［1］。

中值滤波的实质就是排序，排序的算法很多，常见的是“冒泡法”，具体算法在此不再赘述。

1.4 一阶滞后滤波

将描述普通硬件RC低通滤波器特性的一阶滞后方程用差分方程来表示，便可以用软件来实现模拟硬件滤波器的功能。RC低通滤波器的传递函数如公式(1)是

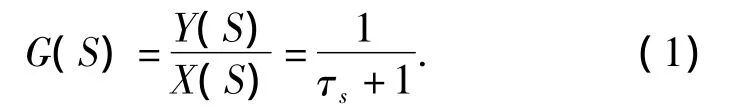
式中τ=RC，为滤波器的时间常数。将上式离散可得其差分方程(2)式:

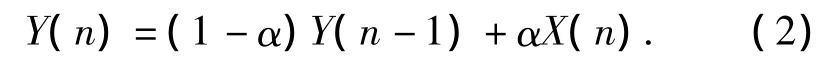
式中:X(n)为本次采样值;Y(n)为本次滤波的输出值;Y(n－1)为上次滤波的输出值;α=1－e－T/τ为滤波平滑系数;T为采样周期。

采样周期T应远小于τ，因此α远小于1。由差分方程可以看出本次滤波的输出值Y(n)主要取决于前一次滤波后的输出值Y(n－1)，本次采样值的影响比较小，这就模拟了具有较大惯性的低通滤波器的功能。

一阶滞后滤波对周期性的干扰具有很好的抑制作用，适用于波动频率较高参数的滤波，但滤波后使相位滞后，响应灵敏度降低，α的大小决定了滞后的程度。

2 改进的滤波方法

2.1 递推平均值法

算术平均滤波法需N次采样后，才能经运算得到一个有效值，速度较慢。为了克服这个缺点，提出了递推平均值原理，即建一个FIFO的队列用来存放N次采样的数据，采得的新数据放入队尾，并丢弃最早的队首数据，然后把队列中的N个数据进行算术平均运算，结果作为有效值。即每进行一次采样就可计算出一个平均值，大大提高了数据处理能力和速度，但算术平均滤波法的其他缺点仍然存在。

这种数据存放方式可以采用环形队列结构来实现，设环形队列地址40H～4FH共16个单元，用R0作队尾指示，其流程图如图2所示。

2.2 中值平均值法

算数平均滤波对抑制随机干扰效果较好，但对脉冲干扰的抑制能力很弱，明显的脉冲干扰会使平均值远离实际值。但中值滤波对脉冲干扰的抑制作用很强，于是可以将两者结合起来形成中值平均值滤波法。中值平均滤波的方法是连续采样N次，去掉一个最大值和一个最小值;然后计算剩余的N－2个数的平均值。中值平均滤波法在许多比赛计分中常常用到。根据其原理可作出程序流程框图如图3。

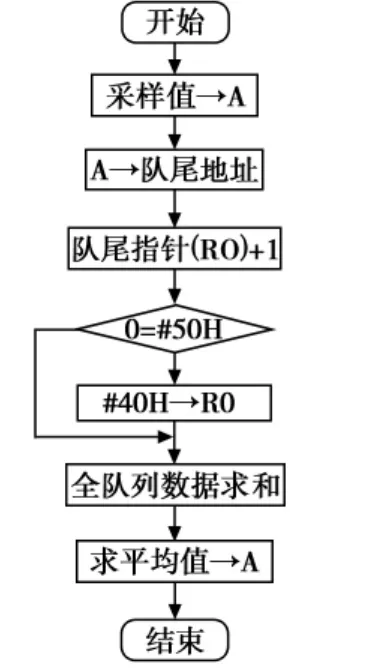
图2 递推平均值滤波

图3 中值平均滤波

还可以将中位值滤波与递推平均值滤波结合起来形成递推中位值平均滤波，这样将进一步优化，既可消除由于偶然出现的脉冲干扰引起的偏差，又提高了运算速度。

2.3 加权平均滤波

平均滤波法的主要缺点是，为了提高对干扰的抑制效果，必须增大平均范围N;但增大N将会引起有用信号的失真，特别是会引起有用信号中高频分量丰富的峰值部位的失真。为协调干扰抑制与信号失真二者之间的关系，可以采用加权的平均滤波法。

所谓加权的平均指，参加平均运算的各采样值按不同的比例进行相加求平均值。加权系数一般先小后大，以突出后几次采样的效果，加强系统对参数变化趋势的辨识。N项加权平均滤波的算法公式如(3)式:

式中C0，C1，…，CN为常数，且应满足 C0+C1+… +CN=1。

2.4 数字滤波的实际应用

用于某型产品的温度监测报警设备，在应用中发现，当开启排风扇甚至开照明灯就会报警，提示舱内温度过高。经分析发现，照明灯和风扇都有储能元件，在开启这些设备时，会有较大的电流，如果走线不合适，就会有很大的干扰耦合进入报警设备，使采样数据超过上限。遗憾的是软件程序也没有采取滤波算法，只要采样到温度超限就报警，等待人来处理。

对于已定型的该产品，进行大的改动明显是很麻烦也是不合适的，如果数字滤波能够满足需要，无疑是最经济方便的了。

我们首先来分析干扰的特点:

只在开启照明灯或排风扇时，干扰出现。那么这个干扰只是脉冲干扰，但还有一点不知道，脉宽，也就是干扰持续时间，不过可以通过计算或试验获得。

再看设备的工作特点:当舱内温度过高时，报警。

由此，我们就可以对程序进行改造了。由于只关心温度超限，那么不超限时可以不予理睬，即不用滤波;当采样到温度超限时，启动滤波程序。由于干扰是以脉冲的形式出现，根据上面对各种滤波方法特性的分析可知，限幅滤波和中位值滤波都能满足要求，但滤波的目的是要躲过干扰，确认温度超限，最好选用限幅滤波的滤波方法。运用方法如下:

首先求几个要用的参数

δA的确定:采样周期T，由工程实践可确定升温速度v，则δA=Tv;

跳出滤波时间(即采样次数)n的确定:脉宽最大值P可由试验求取，并按一定的安全系数确定，n=P/T。

程序流程框图如图4:

图4 温控软件流程图

3 结束语

数字滤波在实际的应用中，究竟用那种滤波算法及应用时机，完全决定于干扰波形的特点和应用目的。总之根据实际情况选用合适的算法，就能达到事半功倍的效果。

［1］赵茂泰.智能仪器原理及应用［M］.北京:电子工业出版社，1999.

［2］张毅刚.MCS-51单片机应用设计［M］.第2版.哈尔滨:哈尔滨工业大学出版社，1997.