公路定线方法的研究

游润卫，杨美荣

(1. 内蒙古科技大学，内蒙古 包头 014010；2. 包头市公路工程质量监督站，内蒙古 包头 014040)

公路定线方法的研究

游润卫1，杨美荣2

(1. 内蒙古科技大学，内蒙古 包头 014010；2. 包头市公路工程质量监督站，内蒙古 包头 014040)

通过案例的方式，对直线型定线和曲线型定线两种定线方法的全过程进行了分析、比较，探讨了目前公路定线设计中对于曲线型定线法认识不足的实际情况．研究表明：对于高等级公路设计、立体交叉设计，以及在复杂地形条件下的其他公路设计，曲线型定线法比直线型定线法具有明显的优越性；随着各种计算机辅助路线设计软件的出现，曲线型定线法将会得到广泛的应用．

直线型定线；曲线型定线；公路定线；案例研究

公路定线的具体操作方法一般有直线型定线法和曲线型定线法．直线型定线法是根据控制点或导向线和相应的技术指标，先定出与地形相适应的一系列直线，然后用适当的曲线把相邻的直线连接起来的传统定线方法．曲线型定线法是根据导向线和地形、地物条件设置合适的圆曲线，然后把这些圆曲线用适当的直线和缓和曲线连接起来，即与传统的先定直线后定曲线相反的以曲线为主的定线法．目前，在设计中多采用直线型定线法，对于曲线型定线法仍然停留在认识状态，笔者通过案例分析研究，对两种定线方法进行比较，以达到合理应用的目的．

1 直线型定线

在某丘陵地区拟设一段路线，如图 1所示．计算行车速度为60,km/h，需经过一村庄并跨越一处河流，通过地形分析，路线宜从谷地通过联系村庄，避开水塘，在河道比较顺直且较窄处通过，由于地形比较简单，适宜采用直线型定线法确定路线[1]．

1.1 确定导线

如图1所示，起点A到JD1的直线和JD1到JD2的直线限制不是很严格，有一定的调整余地．桥位限制比较严格，定线时宜先确定桥轴线DE，在建筑物和水塘之间应综合权衡确定导线BC．JD3可以通过BC与DE交会得出，对于JD2，只能在过限制点B和C的延长线上．JD1与JD2的确定应充分考虑前后线形的匹配，从以下几方面考虑：① 平曲线间必须有足够的直线长度；② 在满足控制点要求的前提下，反复调整交点位置，尽量使路线偏角较小，交点间距较长，以争取较好的线形指标；③ 起点A至JD1为下坡路段，JD1处应避免急弯，以利行车安全；④ 确定交点JD2位置时，尽量避免交点正对山嘴以争取良好的行车视距．

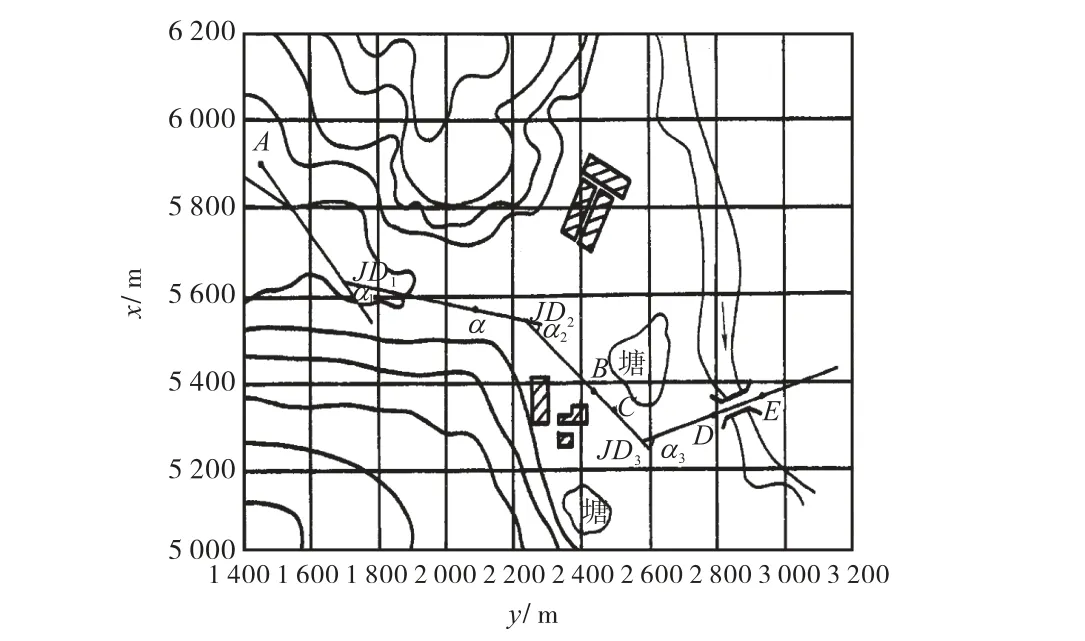
图1 直线型定线法示例

线位确定以后，在地形图上直接采集点位坐标，其中JD2、JD3的坐标不能直接在图上读取，可按解析几何方法计算，结果见表1．

由表 1，可计算各交点间距及路线转角，计算结果见表2．

表1 直线型定线法导线点坐标数据

表2 路线交点间距及路线转角表

1.2 设置平曲线

由于JD1与JD2偏角大致相等，交点间距较长，JD1处地形较陡，应避免出现陡坡与小半径的平纵组合，故平曲线指标可适当取值高一些；JD2与JD3交点间距较短，JD3偏角较大，且弯道内侧正对水塘，路线前方又要跨河，要求桥头引道应尽可能保证直线段长一些为好．据此分析，设置平曲线时应优先考虑JD3，该处平曲线半径R及缓和曲线长度LS需按切线长(T)和外距(E)控制综合考虑确定．

JD3处平曲线要素确定后，随之可按切线长控制确定JD1与JD2的平曲线要素．由于JD1与JD2、JD2与JD3均为反向，可设置为S型曲线或单曲线．如为单曲线，曲线之间直线段长度应满足《规范》要求，否则，应调整交点位置，重新计算．

圆曲线半径R和缓和曲线长度LS确定后，即可计算平曲线要素和推算主点桩号．对于高速公路，还需计算逐桩坐标，计算过程略．

1.3 遵循的原则

路线定线是一个反复比较的过程，为避免不必要的返工，确定交点时均应考虑前后线形的衔接，遵循“定一点，看三点”的原则，每确定一个交点，就要考虑到前方该如何才能合理布线．应注意横向地形、地质、地物控制的要求，做到定的是一条线、考虑的是一条带，从整个路线带范围来布置路线；要充分利用有利地形，尽量避免出现小偏角与“断背曲线”等情况；同时，也要尽量控制路线出现过多的大偏角，导致路线过于曲折、线形指标降低．

2 曲线型定线

拟在某丘陵地区设计一段路线，如图 2所示．计算行车速度为60,km/h，经分析，路线宜在谷地走廊通过，并在顺直河段跨越某河流，但由于地形比较狭窄，采用直线定线法由于所穿交点的位置并不在道路的中线上，难以掌握具体线位，只能估计，远不如曲线定线法直观、方便．

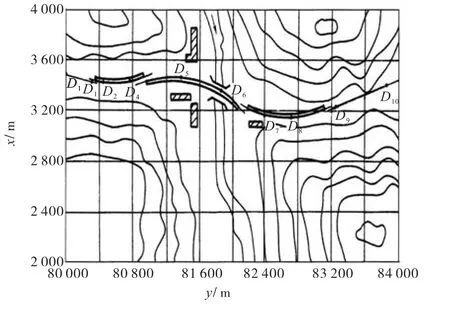
图2 曲线型定线法示例

2.1 确定线形单元

因路线起终点方向已经确定，且路线需穿过某村庄，线形标准不宜过于曲折；跨越河流如采用正桥可能因视距的需要导致拆迁数量过大，有一定的难度．经徒手勾绘路线，路线以较大半径平曲线通过比较适宜，能保证行车安全．根据地形和地物控制点的限制，用直尺和铁道弯尺逼近徒手勾绘的线形，定出符合路线《规范》要求的圆曲线半径，各线形单元之间有错位．然后，采集每一圆曲线和直线上两个点的坐标并计算相邻点连线间距离及方位角，数据如表 3所示．

2.2 回旋线参数及缓和曲线计算

本案例包括由三个平曲线组成的两个反向曲线和两段直线与圆曲线相接的情况．第一个反向曲线半径之比接近1，第二个反向曲线半径之比小于2，均可优先考虑设置为S型曲线，其对应的两个回旋线参数宜相等；如不合适，可分别作为单曲线处理，但应保证曲线间的直线段长度满足《规范》要求．考虑桥位地形，应尽量使桥位全部位于圆曲线内，以方便设计与施工．

表3 曲线型定线法有关采集、计算数据

由于采用近似计算法，其公式的误差大约为3%[2]，故采用解析法试定或试算，把合适的缓和曲线固定下来，形成连续的平面线形．

为便于区分，除已知点D1～D10外，以下计算字符下标i表示第i个曲线元素，下标i-j表示第i个曲线元素第j个缓和曲线部分对应的计算要素；D3与D4，D5与D6，D7与D8所在圆曲线分别表示为⊙M1、⊙M2、⊙M3．

(1) 计算各圆曲线的圆心坐标如表4所示．

(2) 计算直线与圆曲线、圆曲线与圆曲线的间距(通过Excel或牛顿求根法试算)如表5所示．

(3) 计算回旋线参数及缓和曲线长度如表6所示．

表4 各圆曲线的圆心坐标

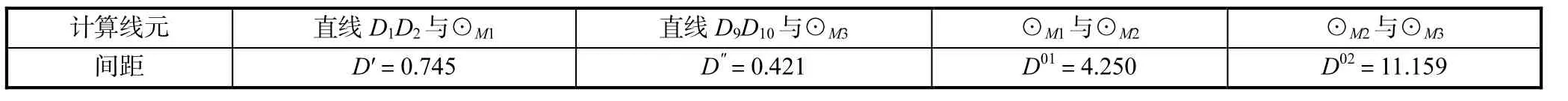
表5 直线与圆曲线、圆曲线与圆曲线的间距 m

表6 直线与圆曲线、圆曲线与圆曲线连接的回旋线参数及缓和曲线长度

2.3 坐标计算

本计算机针对第一个曲线，通过 HY1-1的切线支距坐标，及ZH1-1点到圆心M1的方位角11ZMα-求得已知点 D3、D4所在平曲线第一缓和曲线起点 ZH1-1、终点HY1-1坐标；通过计算S型曲线对应的公切线Q1Q2方位角，以及相应衔接点D(1)、D(2)、D(3)坐标计算[3]，求得已知点D3、D4所在平曲线第二缓和曲线起点HZ1-2、终点YH1-2坐标，如表7所示．

表7 部分衔接点坐标计算结果

同理，可计算其他各曲线间衔接点坐标，此处从略．

2.4 平曲线长度计算

以 D3、D4所在第一个平曲线为例，由 HY1-1点、YH1-2点坐标计算圆曲线相应弦长Sy1＝554.369,m．

由此，计算圆曲线长度为

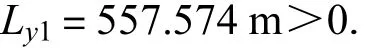
所以，D3、D4所在的第一个平曲线总长为

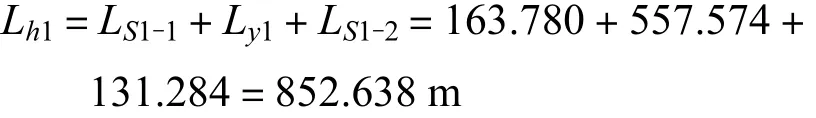
尽管，圆曲线长度所占比例较大(LS1-1∶Ly1∶LS1-2＝1.24∶4.24∶1)，但由于缓和曲线足够长，均满足《规范》要求，故该平曲线设计比较适宜．

同理，可求得 D5、D6所在的第二个平曲线及 D7、D8所在的第三个平曲线总长．

3 结 论

通过以上案例分析，可以看出直线型定线法与曲线型定线法从本质上并无区别，定线成果都是直线、缓和曲线、圆曲线组成的中线，但它们的定线过程、适应地形、视觉效果、设计计算以及使用条件等方面则有所差别，主要表现为以下几点．

(1) 直线型是先定直线，通过直线相交确定交点，用圆曲线或设缓和曲线的圆曲线连接两直线，通常单个平曲线多为基本型对称式．计算时需先确定各转角值及交点间距，各中桩桩号多由交点桩号及切线长度推算，可用于直接定线．这也是习惯采用该方法的主要原因．而曲线型定线法是先定圆曲线，两相邻圆曲线之间用缓和曲线或直线连接，一般不设交点．圆曲线长度由坐标计算，由于直线与圆弧之间的错位不一定相同，以致单个平曲线多为基本型非对称式，基本型对称式出现的几率很小．各中桩桩号完全由曲线或直线长度推算，且不能用于直接定线．此外，对于直线与圆弧之间的错位间距应严格控制，因为按照常规，计算设置缓和曲线后内移值一般不超过2.0,m，否则，线形组合往往达不到理想的效果．

考虑当前我国公路路线设计“图表文件示例”的规定，需填写“直、曲线及转角一览表”，鉴于曲线型定线法不设交点这种情况，可沿用我国公路设计的习惯作法与规定．其方法是将同向平曲线(或反向平曲线)用直尺划线与其圆弧相切并延长，其后圆弧切线与前圆弧切线相交后即为交点(JD)，依次向前并编号[4]，但交点桩号及转角、各曲线切线值、外距值、交点间距可不必给出，否则需准确确定交点位置．填表时各曲线主点桩号需完整．

(2) 在地形简单、地物少的地区及城市郊区，由于一般均按直线形规划，采用直线型定线法比较适宜．但对于地形或地物较为复杂的地段，要做到较好的适应地形地物的要求，则需要经过反复多次调试，有时还不能完全达到预期目的[5]．特别是山岭重丘地区，其复杂变化多端的地形、地势，采用多型曲线予以组合、匹配成连续曲线，将更能满足高速驱车行驶的视线要求和视觉需要[6]．同时，曲线型定线比强拉直线更能减少土石方工程数量．尤其对于立体交叉匝道的线性设计，直线型定线法在这方面更是有明显的不足．

(3) 曲线型定线法必须在大比例尺的准确程度高的地形图进行纸上定线，需要用铁道弯尺、计算机和用于计算的一套程序，其设计计算和放线要比直线型复杂．由于各种计算机辅助路线设计软件的出现，有效地解决了外业勘测设计过程中无法快速、准确计算除对称常规曲线外的复杂线形逐桩坐标的困难，使曲线法定线成为可能．

［1］孙家驷. 道路勘测设计[M]. 2版．北京：人民交通出版社，2006.

［2］汉斯·洛伦茨． 公路线形与环境设计[M]. 骍尹家 ，译. 北京：人民交通出版社，1988.

［3］杨少伟. 道路勘测设计[M]. 3版．北京：人民交通出版社，2009.

［4］宋嘉男，赵春菲. 浅谈高等级公路纸上定线与路线方案的拟定[J]. 黑龙江交通科技，2007(9)：22-23．

［5］何 杰，邢长春，杨华仕. 高等级公路曲线定线法的优越性[C]// 第十届中国科协年会论文集．北京：中国科学技术协会声像中心，2008：448．

［6］胡江碧，刘运通，费雪良. 一种简便实用的平面线形曲线定线法[J]. 北京工业大学学报，2001，27(1)：116-118．

Study on Method of Highway Alignment

YOU Run-wei1，YANG Mei-rong2
(1. UST Inner Mongolia，Baotou 014010，China；2. Highway Engineering Quality Supervision Bureau of Baotou，Baotou 014010，China)

Through case studies，this paper analyzes the methods of linear alignment and curvilinear alignment，and discusses the actual situation for study on the method of highway alignment.The results show that the method of curvilinear alignment has an advantage over the method of linear alignment in designing highway，three-dimensional crossroad and other highway under the conditions of complex topography.As different versions of computer-aided route design software are created，the method of curvilinear alignment will be widely used.

linear alignment；curvilinear alignment；highway alignment；case study

U491.234

A

1006-6853(2010)04-0264-04

2010-08-16；

2010-09-20

游润卫（1965—），男，内蒙古包头人，内蒙古科技大学副教授，硕士．

（编辑：张兰娜）