戴河大桥简支系杆拱桥预应力对自振特性影响研究

李自林，高国勋，恽振波

(1. 天津城市建设学院，天津 300384；2. 中铁六局集团天津铁路建设有限公司，天津 300232)

戴河大桥简支系杆拱桥预应力对自振特性影响研究

李自林1，高国勋1，恽振波2

(1. 天津城市建设学院，天津 300384；2. 中铁六局集团天津铁路建设有限公司，天津 300232)

利用有限元分析软件 ANSYS对天津至秦皇岛客运专线戴河大桥的钢管混凝土简支系杆拱桥进行建模，对该桥梁模型进行模态分析，提取了桥梁在无预应力、0.5倍预应力、全预应力三种情况下前十阶的自振频率，分析了预应力对结构阵型和频率的影响，得出结论：预应力的施加对桥梁的振型影响不大，但是会使桥梁的竖向自振频率略微降低，扭转自振频率略有提高，拱肋的振动也有不同程度的提高．

钢管混凝土；简支系杆拱桥；自振特性；戴河大桥

近年来下承式钢管混凝土拱桥以其形式优美、结构受力合理而被广泛应用，下承式钢管混凝土系杆拱桥是多次超静定结构，结构工作在几何非线性状态．目前，对该类桥梁的静力行为研究相对较多，研究成果集中在结构的极限承载力、稳定性、徐变影响等领域．但是，对承式钢管混凝土系杆拱桥在地震、车振、风振作用下的动力问题研究相对较少，这些问题是结构设计无法回避的．结构的自振特性分析是结构动力分析的基础，不管对哪种动力问题进行计算分析，都要对结构的自振特性做深入的研究．目前，除了实测获得钢管混凝土拱桥自振频率外，还可以通过有限元程序求解钢管混凝土拱桥的动力性能，许多实例[1-4]已表明，有限元计算结果和实测值比较接近，因此用有限元建模分析结构的动力特性，能够较好地反映结构的实际状况．由于下承式钢管混凝土系杆拱桥的研究相对较少，故笔者以单跨 58,m 下承式钢管混凝土系杆拱桥为工程背景，利用 ANSYS软件对其进行了模态分析，得出了该桥的前十阶阵型，分析了下承式钢管混凝土系杆拱桥自振特性的一般性规律，并对下承式钢管混凝土系杆拱桥预应力的影响进行了初步的研究．

1 有限元计算理论和方法

有限元的基本思想包括以下三个方面：首先是将结构或连续体的求解域离散为若干个子域(单元)；其次用每个单元内设的近似函数来分片表示全求解域内待求解的未知场变量；最后是通过和原问题数学模型(例如基本方程和边界条件)等效的变分原理或加权余量法建立求解基本未知量(场函数节点值)的代数方程组或常微分方程组．模态分析也包括以上三个有限元基本思想．模态分析时只需建立钢管砼拱桥的自由振动方程，即

式中：M为质量矩阵；K为刚度矩阵；u为位移向量．若假定为谐运动，模态分析的运动方程可以转化为

由结构动力学知识可知，结构的位移和内力通常由前几阶自振频率和相应振型起着控制作用，因此求得前几阶振动频率和相应振型便可以对结构做出很好的分析评价，目前常采用子空间迭代法来计算[5-8]．

2 工程概况及有限元建模

2.1 工程概况

戴河大桥为新建天津至秦皇岛客运专线上跨戴河而设的简支系杆拱桥．该桥中心里程为DK249+462.3，孔跨样式为两跨，每跨为 56,m，全桥长133.2,m．桥梁与水流方向成 55°夹角．桥梁各部件的具体参数如下．

(1) 拱肋．梁全长 58,m，计算跨度为 56,m，矢跨比为 1∶4，拱肋采用二次抛物线，拱肋中心线方程为y＝56(56-x)x/562(见图1)．拱肋横断面采用哑铃型钢管混凝土变截面，拱顶截面高度2.2,m，拱脚截面高度2.8,m，钢管直径为1,m，由厚14,mm 的钢板卷制而成，每根拱肋的两根钢管之间用厚14,mm的腹板连接，拱管内灌注C50补偿收缩混凝土．两拱肋中心距11.8,m．

(2) 横撑．拱肋之间设五道一字形横撑，横向风撑采用外径1,m的圆形钢管，钢管内不填充混凝土．

(3) 吊杆．吊杆采用平行布置，间距 4,m，全桥共设11对吊杆，铅垂布置．采用PES(FD)7-61平行镀锌高强平行钢丝束，配套使用OVMLZM- 6 1G(L)型冷铸锚，吊杆穿过拱肋锚于拱肋上缘张拉底座，下端锚于箱梁下缘固定底座．

(4) 梁．梁采用单箱五室预应力混凝土箱型截面，梁高1.4,m，顶板厚0.35,m，底板厚0.35,m，边腹板厚 0.8,m，中腹板厚0.35,m，中横隔厚0.4,m，边横隔厚3,m．梁部不设检查孔，底板设泄水孔，边腹板和中腹板设通气孔．桥面宽度：防护墙内侧净宽 8.8,m，桥面板宽16,m．

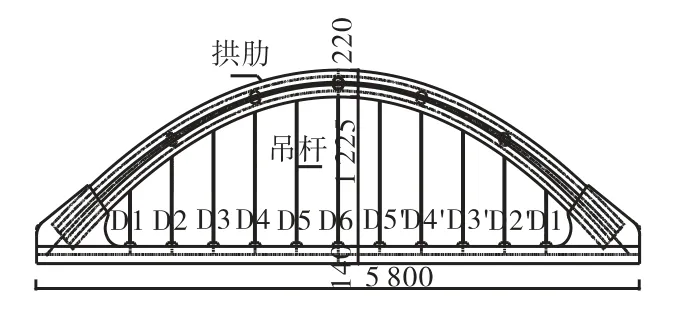
图1 实际桥梁简图(单位：cm)

2.2 有限元建模

正确建立钢管混凝土拱桥有限元模型首先就是对拱肋进行模拟．对拱肋模拟的方法一般有：①双单元法，就是将钢管和砼分别作为两个杆件，但使其节点坐标相同；②换算截面法，将钢管砼截面中的钢材换算成相当的砼截面；③用钢管砼统一理论[8-11]方法．笔者利用 ANSYS中的梁单元 BEAM44，建立拱肋双单元法梁模型．

吊杆采用 LINK10单元，横撑采用 BEAM44单元模拟，梁采用 SOLID45单元与 SHELL63单元模拟，两单元交接处做面耦合处理．桥面梁之所以用两单元模拟是因为在桥梁的两端各有一实体部分，而中间段为单箱五室箱梁．吊杆与梁交接点采用节点耦合处理．材料常数如表1所示．

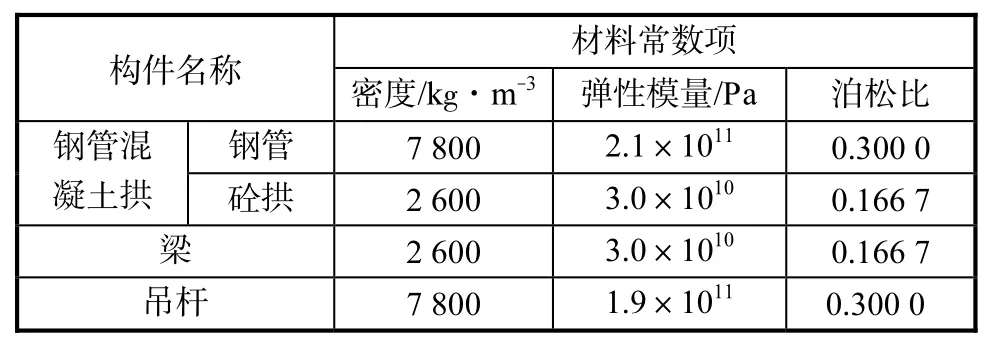
表1 材料常数

3 计算结果及数据分析

由结构动力学知识可知，实际桥梁结构的动力性能一般由其前几阶阵型所决定，故笔者利用大型有限元分析软件ANSYS分别提取了戴河大桥无预应力模型、0.5倍的全预应力模型、全预应力(12,515.37,kN)模型的前十阶自振频率和阵型图，分别见表2和图2所示．该桥共有 53根预应力钢丝，施加预应力时首先根据预应力钢丝的位置来确定模型中相应的节点，然后对节点直接施加预压应力．

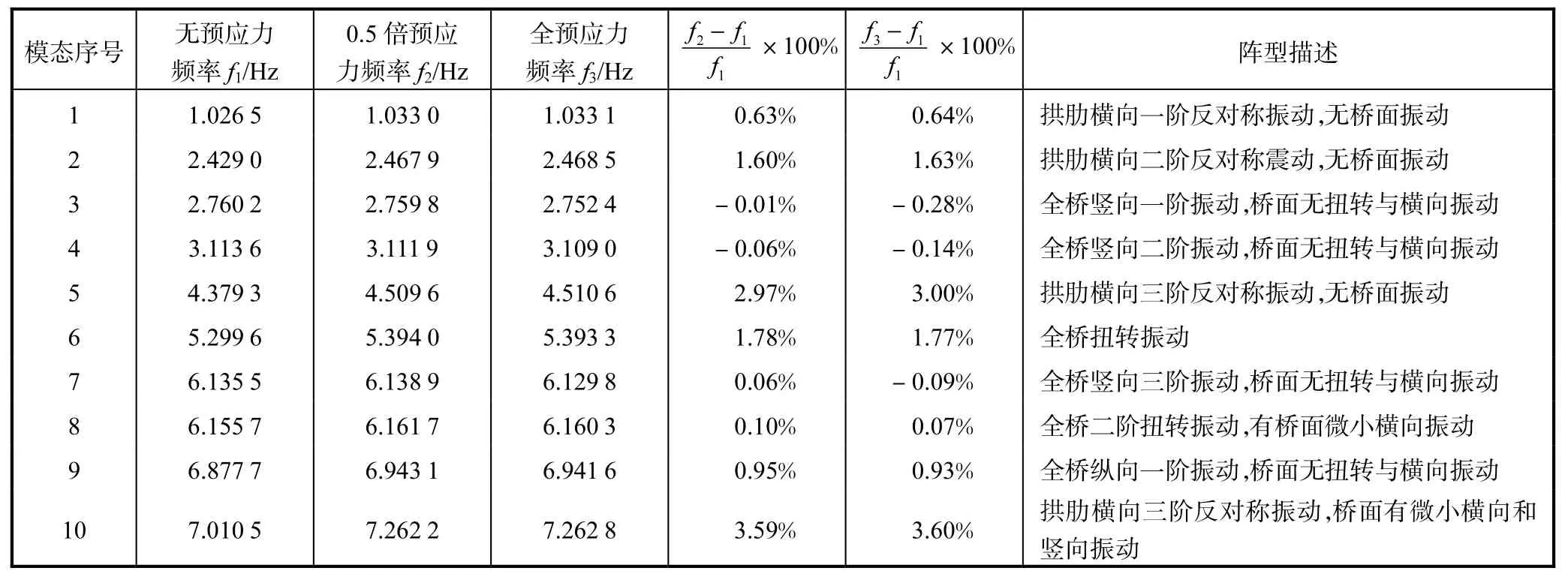
表2 简支系杆拱桥三种预应力状态下自振特性计算

由表 2及图 2的阵型图可以看出该简支系杆拱桥的阵型比较复杂，总的特点如下：①无论是否有预应力，结构的十阶阵型基本不变，只是频率有略微改变，主要振动形式有：拱肋的振动、桥面的振动及拱肋和桥面的耦合振动；②前十阶阵型中基本上没有桥面的横向振动(个别的有微小横向振动)，可见桥面的横向刚度很大，这与实际是吻合的，该桥梁采用单箱五室箱梁，使得横向惯性矩很大，从而很好地提高了桥面的横向刚度；③预应力的施加使得桥梁的扭转自振频率有不同程度的提高，这在表2中6，8两组数据中都有体现；④由表 2中3，4两组数据可知预应力的施加使得桥梁的竖向自振频率略微降低，降低量都小于0.3%，这是因为预应力的施加虽然提高了结构的弹性刚度，但却降低了其几何刚度[12]；⑤由表2中3这组数据可知桥的竖向一阶自振频率为2.752,4,Hz，完全满足戴河大桥梁竖向的自振频率不低于1.883,Hz的设计要求；⑥该桥除最小自振频率 1.033,1,Hz(拱肋横向一阶反对称振动频率)有些偏柔性(可以通过多设横撑加以改善)，其余自振频率都在 2.4,Hz以上，这比一般的钢管混凝土拱桥大了许多，由此可见该桥的整体刚度很大，设计偏于安全．

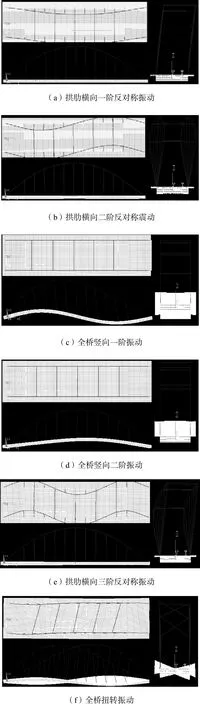
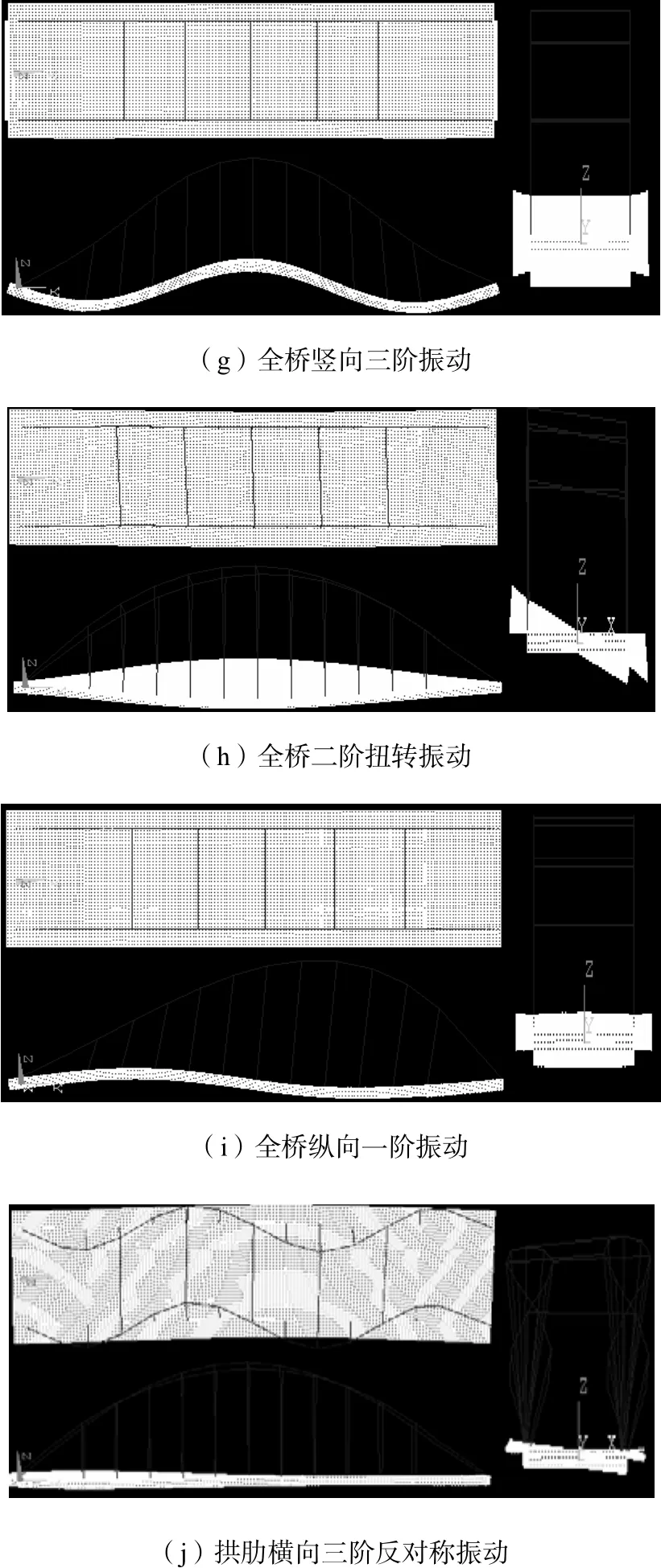
图2 简支系杆拱桥在设计预应力(即全预应力)下的十阶阵型

4 结 论

通过ANSYS模拟戴河大桥做有限元计算与分析可以得到以下结论．

(1) 有无预应力对桥梁的阵型影响不大，但是预应力的施加会使桥梁的竖向自振频率略微降低，降低量都不大于 0.28%，而扭转自振频率略有提高，提高量为 1.77%(全预应力)，箱梁预应力的施加使得拱肋的振动有不同程度的提高，提高范围在 0.6%～3.6%之间．

(2) 该桥的振动形式大致可分为三种：拱肋的振动、桥面的振动及拱肋和桥面的耦合振动．值得注意的是该桥的一阶频率为拱肋横向一阶反对称振动，拱肋为该桥最柔的一部分，在动力响应分析中很可能是最先破坏的一部分．

(3) 该桥整体刚度较大，特别是箱梁的刚度较大，从自振频率都大于2.4,Hz上来看，该桥的刚度较大，设计偏于安全．

［1］袁海庆，周强新，范剑锋. 钢管混凝土施工控制可视化仿真计算系统[J]. 武汉理工大学学报，2003，25(10)：54-56.

［2］项海帆，刘光栋. 拱结构的稳定与振动[M]. 北京：人民交通出版社，1991．

［3］许士杰. 钢管混凝土肋拱桥自振特性及汽车荷载作用下动力响应的研究[D]. 北京：北方交通大学，1999.

［4］张明远，王学国，江志学，等. 钢管混凝土拱桥拱肋吊装几何非线性分析[J]. 武汉理工大学学报，2003，25(9)：40-42.

［5］石 洞，石志源，黄东洲. 桥梁结构电算[M]. 上海：同济大学出版社，1987.

［6］段 进，倪 栋，王国业. ANSYS10.0结构分析从入门到精通[M]. 北京：兵器工业出版社，2006.

［7］李卫民，杨红义，王宏祥，等. ANSYS工程结构实用案例分析[M]. 北京：化学工业出版社，2007.

［8］李枝军，李爱群，韩晓林. 润扬大桥悬索桥动力特性分析与实测变异性研究[J]. 土木工程学报，2010(4)：92-98．

［9］CECS28：90，钢管混凝土结构设计与施工规程[S].

［10］贺国京，黄 伟. 大跨度钢管混凝土拱桥空间地震响应分析[J]. 中南林业科技大学学报，2008，28(5)：119-122.

［11］钟善桐. 钢管混凝土统一理论——研究与应用[M]. 北京：清华大学出版社，2006.

［12］贾艳敏，王佳伟，韩基刚. 预应力简支钢箱梁固有频率影响因素分析[J]. 工程力学，2009，26(6)：37-40.

Research on Influence of Pre-stress on Self-vibration Characteristic of Dai He Simply Supported Tie-Bar Arched Bridge

LI Zi-Lin1，GAO Guo-Xun1，YUN Zhen-Bo2
(1. Tianjin Institute of Urban Construction，Tianjin 300384，China；2. Tianjin Railway Construction Co.，Ltd，China Railway Sixth Group，Tianjin 300232，China)

By using finite element analysis software ANSYS, this paper develops a modeling framework for the Dai He Simply Supported Concrete-filled Steel-tabular Tie-bar Arched Bridge which is one part of the Tianjin to Qinhuangdao passenger special line. Through model analysis, the self-vibration frequencies of this bridge's anterior ten steps were extracted in three cases: no pre-stress, a half pre-stress and full pre-stress. By analyzing the influence of pre-stress on the structural vibration mode and frequency, the paper came to the conclusion that with little effect on the vibration mode of the bridge, the pre-stress on the bridge will slightly reduce the frequency of vertical vibration, more or less heighten the frequency of torsional vibration and increase the vibration of arch in different degrees.

steel pipe-encased concrete；simply supported tie-bar arched bridge；self-vibration characteristic；Dai He bridge

U448.225

A

1006-6853(2010)04-0237-04

2010-09-08；

2010-10-11

中铁六局集团有限公司科技项目(2010-1-A04)；天津市自然科学基金资助重点项目(08JCZDJC18300)

李自林（1953—），男，河北成安人，天津城市建设学院教授，天津大学博士生导师.

（编辑：胡玉敏）