戴河大桥钢管混凝土系杆拱内力及应力解析解研究

高伟明，何 震，刘 振

(1. 天津城市建设学院，天津 300384；2. 中铁六局集团天津铁路建设有限公司，天津 300232)

戴河大桥钢管混凝土系杆拱内力及应力解析解研究

高伟明1，何 震2，刘 振2

(1. 天津城市建设学院，天津 300384；2. 中铁六局集团天津铁路建设有限公司，天津 300232)

利用对称性对戴河大桥空间结构进行了简化，通过计算得出钢管混凝土系杆拱桥在成桥后的解析解，对关键截面进行了受力验算，并与其容许值进行比较，验算了各关键截面的安全性．提出钢管混凝土系杆拱简化计算的一般模式，为手算钢管混凝土系杆拱内力和应力情况提供参考．

钢管混凝土系杆拱；内力计算；应力计算；解析解

1 工程概况

戴河大桥位于新建天津至秦皇岛高速客运专线上，跨越戴河，设计时速为350,km/h，本桥设计为下承式后张预应力为2孔56,m的钢管混凝土简支系杆桥拱，轨道类型采用 CRTS-Ⅱ型板式无砟轨道．梁全长58,m，计算跨度为 56,m，矢跨比 f/l＝1∶4，拱肋平面内矢高 14,m，拱肋采用二次抛物线，拱肋中心线方程为：y＝56(56-x)x/562，桥梁立面图如图 1所示．拱肋横断面采用哑铃型钢管混凝土变截面，拱顶截面高度h＝2.2,m，拱脚截面高度 h=2.8,m，钢管直径为 1,m，由厚 14,mm 的钢板卷制而成，每根拱肋的两钢管之间用厚度为14,mm的腹板连接．每隔一段距离，在圆形钢管内设加劲箍，在梁腹板中焊接拉筋．两拱肋中心距11.8,m．拱管内灌注C50补偿收缩混凝土，钢管拱内混凝土灌注采用泵送顶升法浇注．

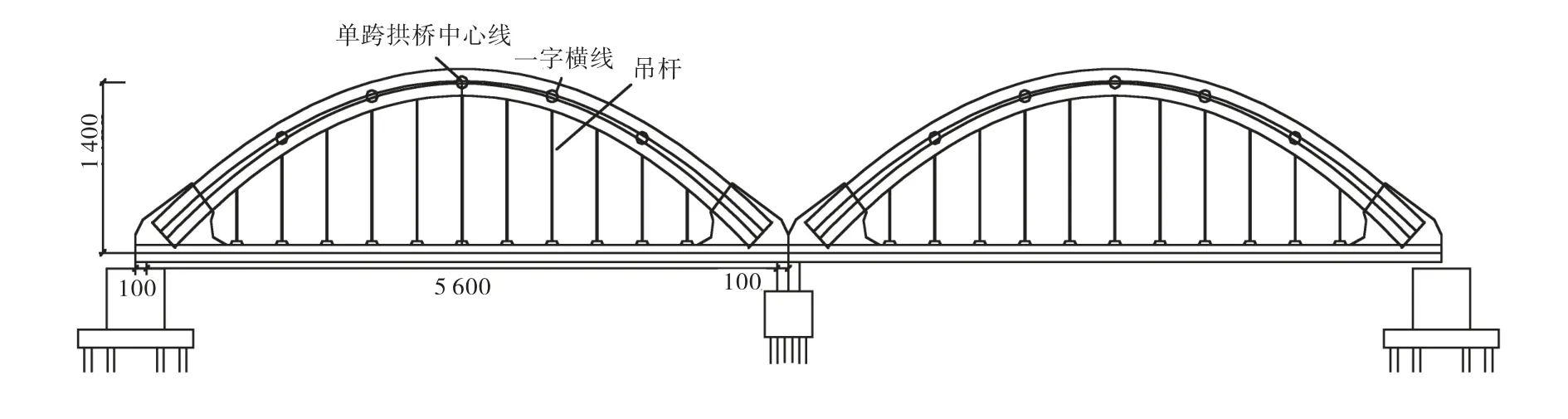
图1 桥梁立面图(单位：cm)

2 结构简化

对戴河大桥原结构进行合理简化，取其中一跨的半边结构，使其成为适合手算的平面多次超静定结构，如图2所示．结构简化后的各种参数选取如下．

(1)钢管混凝土拱(横截面见图 3)和钢筋混凝土行车道梁(横截面见图 4)的截面抗弯刚度 EI的取值．对于行车道梁，由于钢筋所占的面积很小，故 E值按混凝土的数值选取，取为 3.45×104,N/mm2，经计算行车道梁抗弯刚度为 9.21×104,N·mm2．对于钢管混凝土拱，由于是由钢管和混凝土共同组成，因此EI选取要考虑两种不同材料的叠加，由于刚度大，超静定结构产生的附加内力也大，因此内力计算时刚度宜取大值[1]，即按中国 CECS28∶90和英国 BS5400标准，采用钢管与混凝土刚度直接叠加的方法[2-3]，其计算公式为

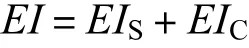
由于腹板截面为变截面，故EI也不是一常数，由于截面面积只是在腹板处发生变化，而在圆截面处不发生变化，所以在上下圆截面处抗弯刚度为一常数，即为

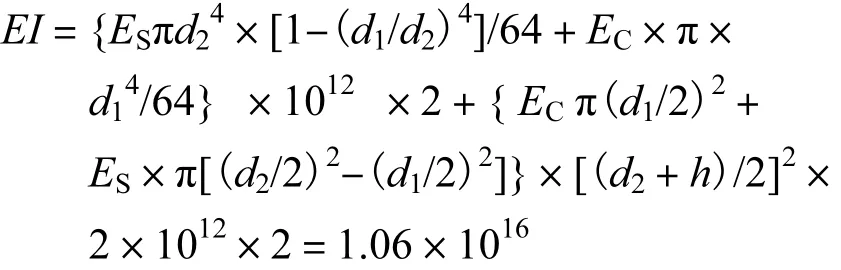
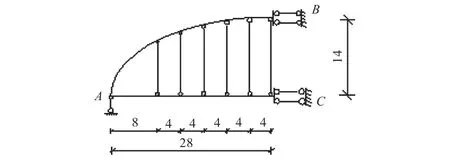
图2 简化后的半边结构(单位：m)

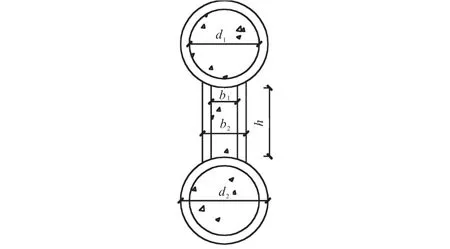
图3 钢管混凝土系杆拱横截面

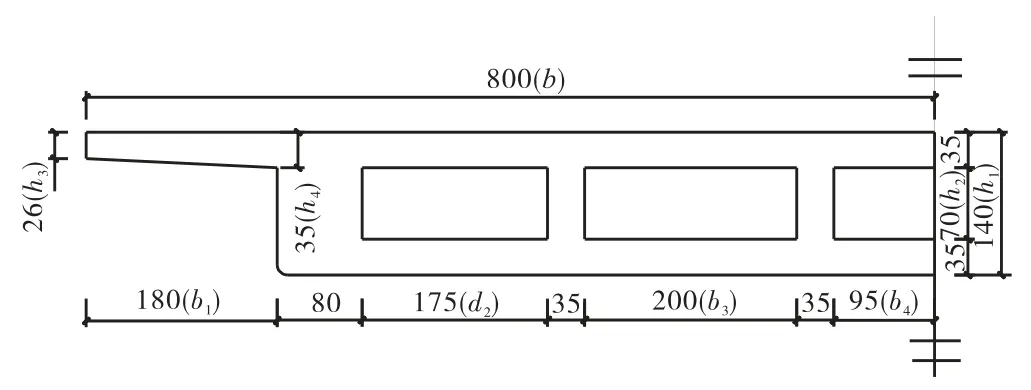
图4 行车道梁横截面(单位：cm)

根据设计说明，截面面积只在腹板处发生变化，腹板厚度保持不变，腹板高度按一次函数变化，在x＝0(即拱脚)处腹板高度为 0.8,m，在 x＝28(即拱顶)处腹板高度为 0.2,m，所以腹板高度随 x变化的一次函数为

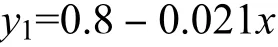
腹板抗弯刚度随x变化的函数式为

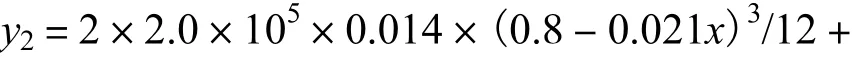
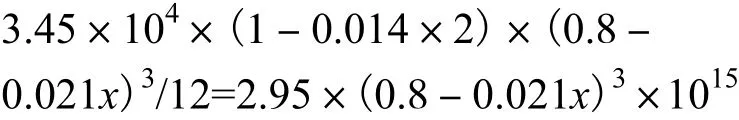
由此得到系杆拱的抗弯刚度为

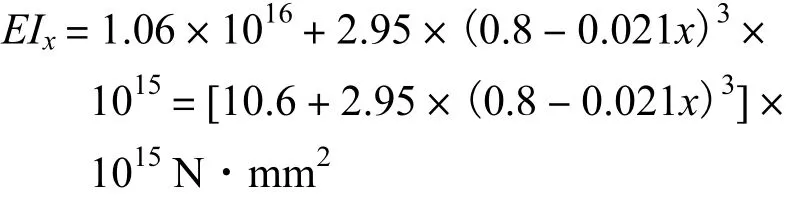
(2) 钢管混凝土拱和钢筋混凝土行车道梁的截面抗拉压刚度EA的取值．行车道梁截面积为

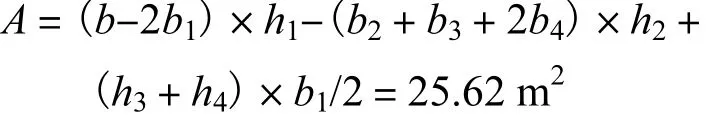
因为笔者取桥梁的半边结构，所以取整体行车道梁面积的一半，故行车道梁抗拉压刚度

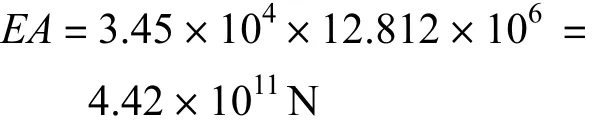
对于钢管混凝土拱，上下圆截面拱肋抗拉压刚度为

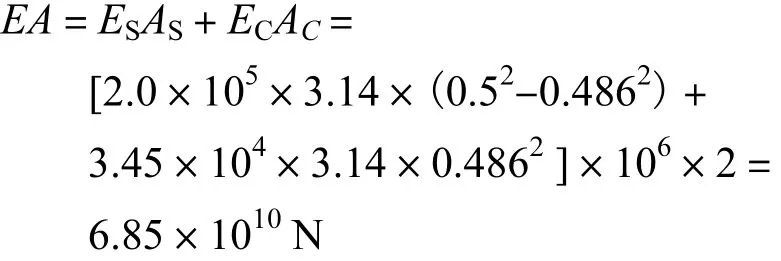
腹板在拱脚处的抗拉压刚度为

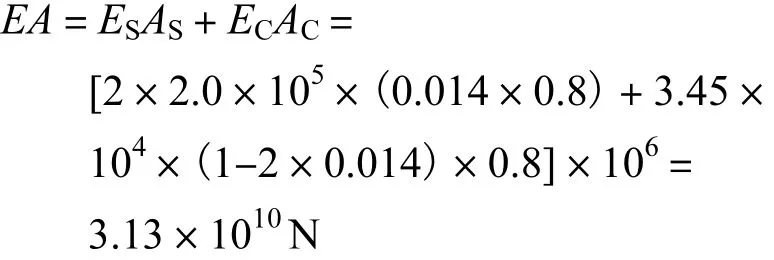
腹板在拱顶处抗拉压刚度为

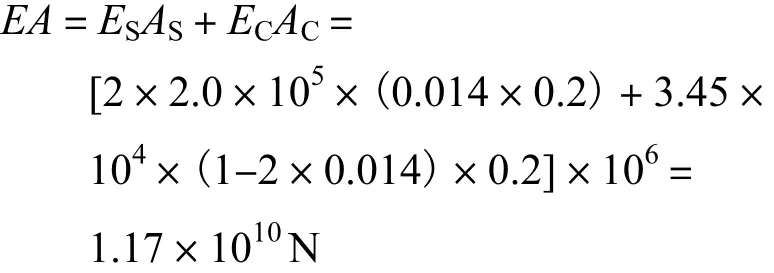
因为腹板高度按一次函数变化，所以腹板抗拉压刚度也可用一次函数拟合，再加上上下圆截面拱肋的抗拉压刚度，得到系杆拱抗拉压刚度为

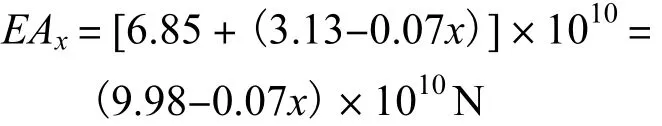
(3)成桥后荷载的取值．根据设计说明，成桥后作用在拱肋上的均布荷载为 35.14,kN/m，作用在行车道梁上的均布荷载为219.72,kN/m ．

手算分析采用力法[4-5]，简化后的结构为 8次超静定结构，设 8个基本未知量分别为 X1，X2，X3，X4，X5，X6，X7，X8，如图 5 所示．

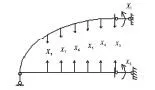
图5 基本未知量

3 内力计算

列立法方程组，有

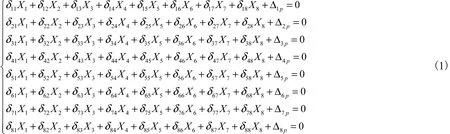
因为此拱桥矢跨比 f/l=1∶4，当 f/l＞1∶5时，δij的计算要考虑弯矩和轴力作用，Δip的计算只需考虑弯矩作用[5]，故可知

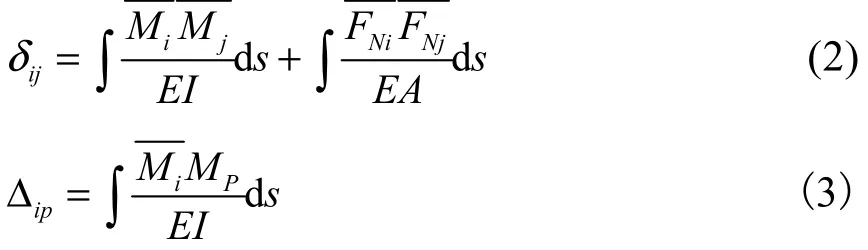
将结构中拱段用AB表示，梁段用AC表示(见图2)．将各段的EI值与EA值代入公式(2)和(3)有

各柔度系数和自由项计算如下

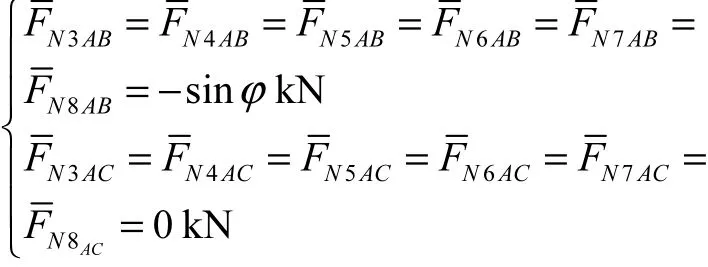
将Mip，，，，分别代入式(4)和式(5)中，经计算得到 δij和Δip，将计算结果列于表1和表2中．

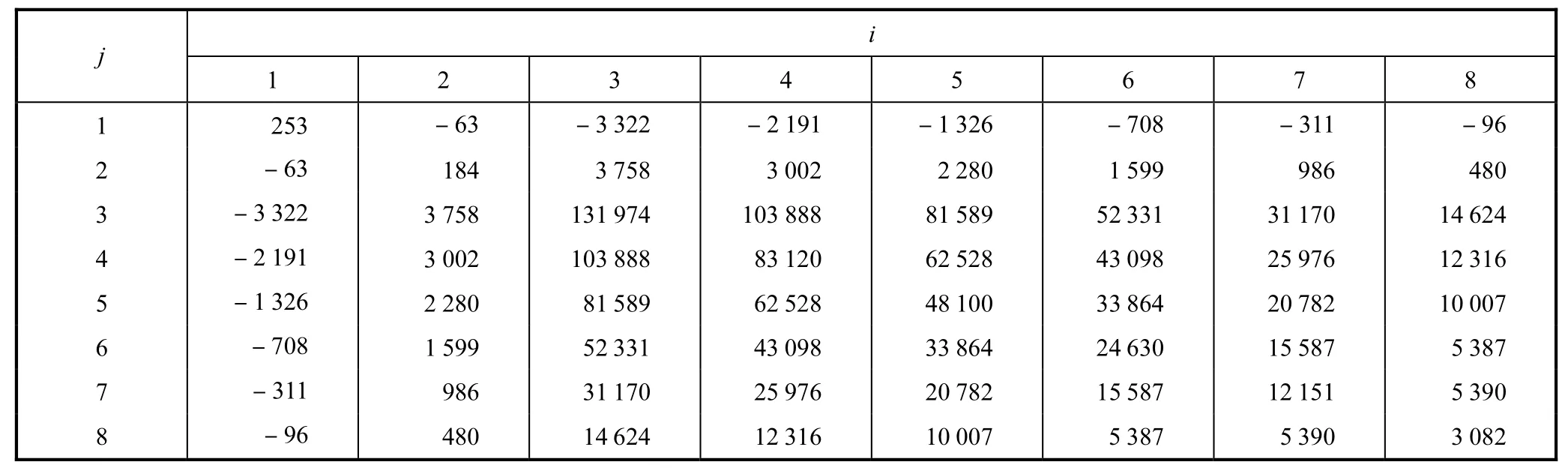
表1 柔度系数ijδ

表2 自由项Δip

将δij和Δip代入式(1)中，解得各基本未知量，列 于表3中．

表3 基本未知量Xi

选取 6个具有代表性的截面，即 1-1，2-2，3-3，4-4，5-5，6-6截面，如图6所示，根据以求得的基本未知量计算出6个截面的内力，计算结果列于表4(M以拱肋下部受拉为正，上部受拉为负，FN以拉力为正，压力为负，FQ以使杆端逆时针方向转动为正，顺时针方向转动为负)．

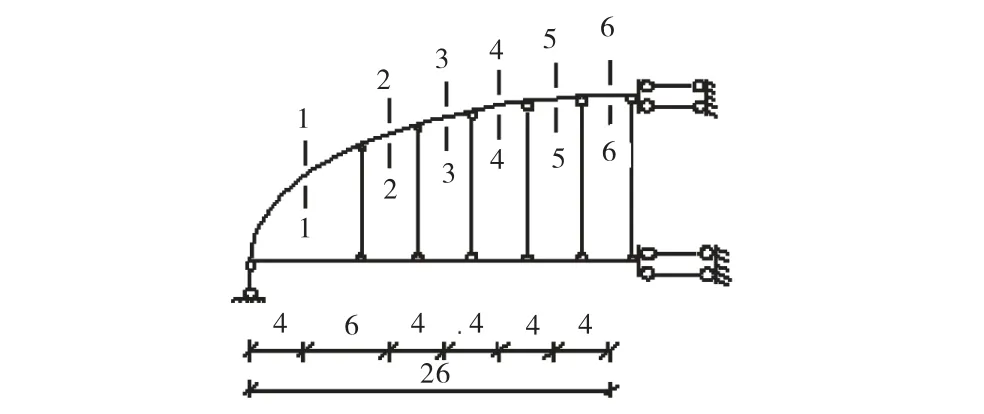
图6 选取截面位置示意图(单位：m)

从表4中可以看出，越接近拱脚截面内力越大．

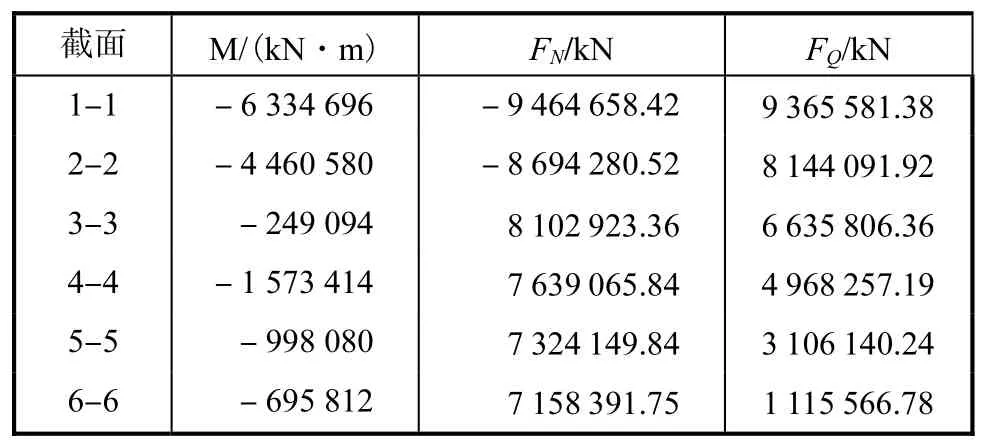
表4 代表截面的内力计算结果

4 应力计算

4.1 由弯矩M产生的正应力

因为拱肋是由钢管和混凝土两种不同材料组成，故在求应力时首先选取混凝土为标准材料，将钢管换算成混凝土[6]，具体过程如下：

根据钢管的弹性模量 Es与标准材料即混凝土弹性模量Ec之比，即n＝Es/Ec得钢管换算后的截面惯性矩为Is，＝nIs，所以组合截面换算后的截面惯性矩为I0＝Ic+nIs，式中：Ic，Is分别为混凝土和钢管的惯性矩．

以组合截面的几何特性计算出应力σ后，标准材料混凝土应力为σc，钢管的实际应力σs=nσ．钢管和混凝土弹性模量之比

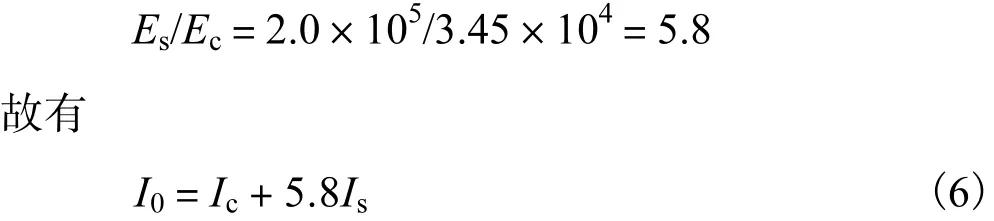
根据式(6)即可算出各截面的惯性矩Iz．

最大正应力σmax＝Mzymax/Iz，其发生在拱肋上下边缘处，计算各个截面的ymax与截面上下边缘处的σmax，结果列于表5(正应力以拉力为正，压力为负)．

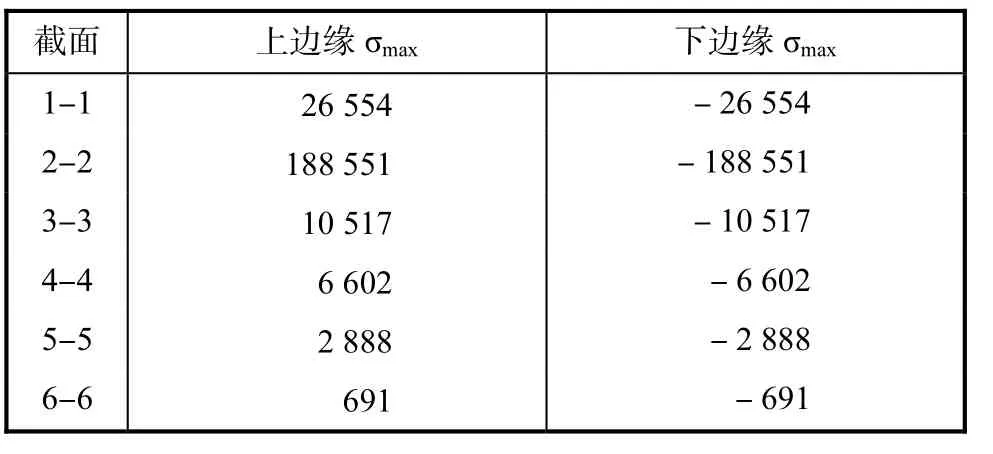
表5 代表截面上下边缘应力σ kN·m2

换算后截面上正应力在y方向上呈线性分布，得到正应力σ后，混凝土各处的正应力σc按照其对应的y值按比例求得，可以求得混凝土最大正应力，钢管各处应力σs＝5.8σ，因为混凝土和钢管最大应力均发生在上下边缘处，将混凝土和钢管上下边缘处应力计算结果列于表6．

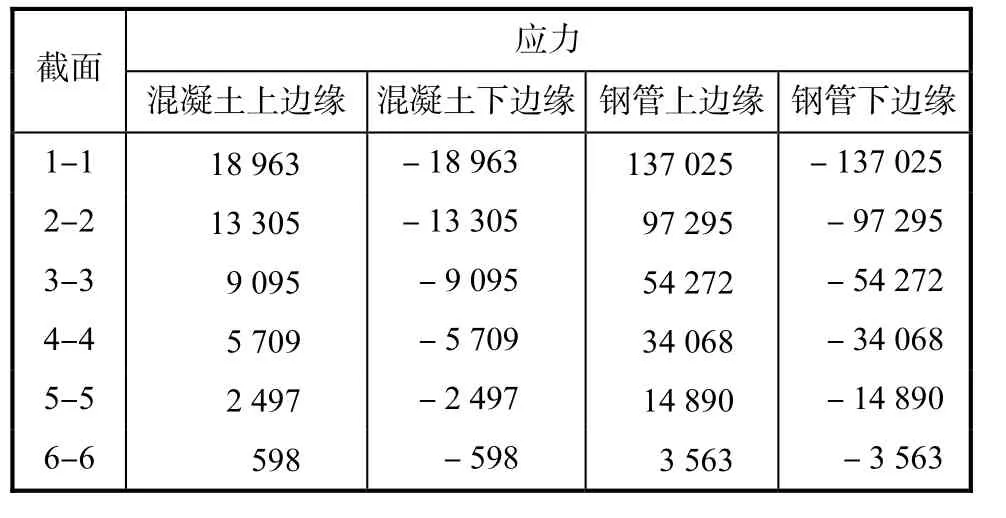
表6 混凝土和钢管上下边缘处应力 kN·m2

4.2 由压力FN产生的正应力

内力FN也会产生正应力，根据文献[7]，将钢管混凝土截面积换算成

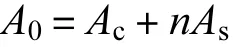
式中：Ac，As分别表示混凝土和钢管的截面积．

由FN产生的正应力σ＝FN/A0，σ即为FN在混凝土截面产生的正应力，而由FN在钢管截面产生的正应力σs=nσ，将由内力FN在混凝土和钢管截面产生的正应力计算结果列于表7．

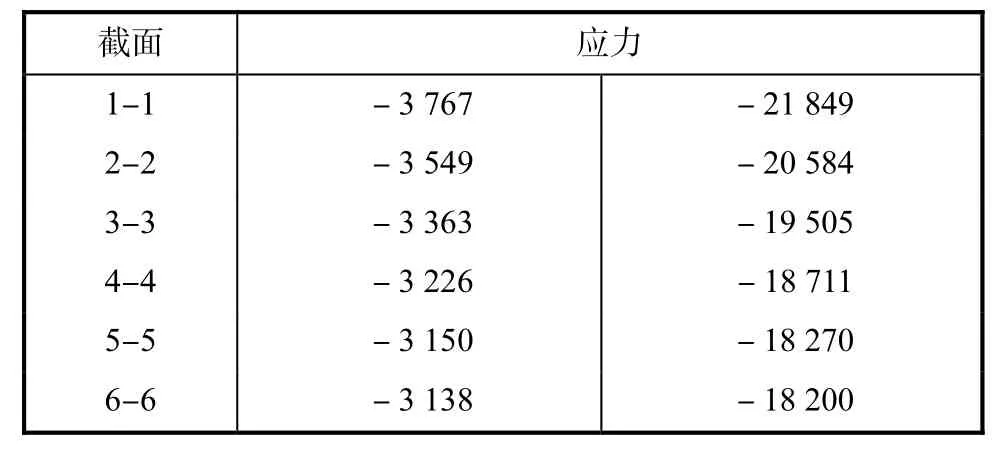
表7 由FN在混凝土和钢管截面产生的正应力 kN

由弯矩M和FN共同作用在拱肋上下边缘所产生的正应力计算结果列于表8．

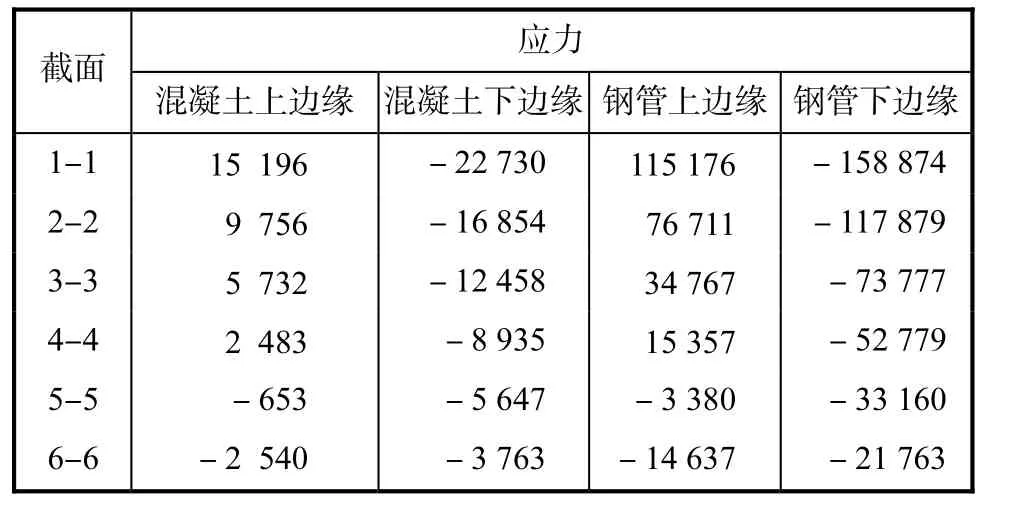
表8 截面正应力计算结果 kN/m2

从表8中可看出，同内力一样，越接近拱脚，截面正应力越大．钢管截面最大受压正应力为 158,874,kN/m2＝158.874,N/mm2＜300,N/mm2；最大受拉正应力为 115,176,kN/m2＝115.176,N/mm2＜300,N/mm2，均小于容许应力．混凝土截面最大受压正应力为22,730,kN/m2＝22.73,N/mm2＜32.4,N/mm2，小于容许应力，但最大受拉正应力为 15,196,kN/m2＝15.196 N/mm2＞2.64,N/mm2，大于容许应力，可知有些截面混凝土上边缘受拉开裂．

5 结 论

笔者通过对戴河大桥原结构进行合理简化，运用手算形式得到结构内力和应力解析解，在桥梁设计广泛采用有限元软件的情况下，解析解能够从理论上对有限元软件的计算结果提供参考和支持．

［1］陈宝春. 钢管混凝土拱桥计算理论研究进展[J]. 土木工程学报，2003，36(12)：47-57．

［2］BS5400. British Standards Institutions [S]．

［3］陈宝春. 钢管混凝土拱桥设计与施工[M]. 北京：人民交通出版社，1999.

［4］陈宝春. 钢管混凝土拱桥的设计计算[J]. 工程力学，1997，2(增刊)：450-454．

［5］朱慈勉. 结构力学[M]. 北京：高等教育出版社，2004.

［6］范立础. 桥梁工程[M]. 北京：人民交通出版社，2001.

［7］陈宝春. 钢管混凝土拱桥[M]. 2版. 北京：人民交通出版社，2007.

Analytical Solution to the Internal Force and Stress of the Concrete-filled Steel-tabular Tie-bar Arch of Dai He Bridge

GAO Wei-ming1，HE Zhen2，LIU Zhen2
(1. Tianjin Institute of Urban Construction，Tianjin 30084，China；2. Tianjin Railway Construction Co.，Ltd，China Railway Sixth Group，Tianjin 300232，China)

After the simplification of the spatial structure of Dai He Bridge due to its symmetrical characteristic, the analytical solutions to the concrete-filled steel tubular arch bridge are obtained by calculation. And then after checking the stress on the critical cross section, the security of the key sections is testified by comparing with the admissible values.Finally, a general pattern of the simplified calculation of the concrete-filled steel-tabular tie-bar arch is put forward to give reference to the manual computation of the internal force and stress of the concrete-filled steel-tabular tie-bar arch.

concrete-filled steel-tabular tie-bar arch；internal force calculation；stress calculation；analytical solutions

U448.225

A

1006-6853(2010)04-0241-05

2010-09-10；

2010-10-11

天津市自然科技基金重点资助项目(08JCZDJC18300)；中铁六局集团公司科技研究项目(2010-1-A04)

高伟明（1986—），男，河北廊坊人，天津城市建设学院硕士生.

book=263,ebook=103

（编辑：胡玉敏）