从高斯公式到高斯定理＊

陈修芳

（武汉工业学院，湖北 武汉 430023）

俗话说，“数理不分家”，主要是说数学中的理论来源于物理实践，反过来又可以应用于物理。理论上，大学物理教师的主要任务是提出物理概念，建立物理模型，至于模型计算如求导积分等只要交给学生利用数学工具去解决就可以了。

数学中的高斯公式是曲面积分的一个重要公式。设空间区域V由分片光滑的双侧封闭曲面S围成。若函数P，Q，R在V上连续，且有一阶连续偏导数，则：

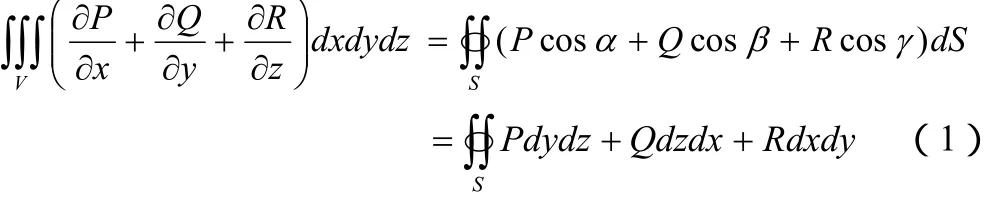
而高斯定理是静电学中的一个重要定理。［2］在静电场中，高斯定理的数学表达式为：

教科书上一般都是利用点电荷的电场线的特点和位于球面球心的点电荷在球面上产生的电通量这个特例及电场线的特点和电场强度的叠加原理来证明高斯定理，［3］这种证明虽然较为简单，但学生较难理解。下面利用高斯公式推导高斯定理：

见图1，闭合曲面为球面S（方程 x2＋y2＋z2＝R2），其所围的立体为V，单位正电荷q放在球心。点电荷在球面上的电场强度为是由点电荷q指向球面的单位矢量。由于球面指向外侧的法向量为故通过高斯面的电通量可写成：

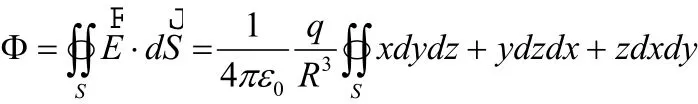
根据高斯公式，有：

若包含点电荷的闭合曲面为任意的，由于电场线不会在无电荷的地方中断，因此，通过任意闭合曲面的电通量与上式相等，若高斯面内包含多个电荷，根据矢量叠加原理，就可以得出高斯定理

图1 高斯面上电场强度示意图

高斯公式和高斯定理虽然表面形式不同，但从高斯公式推导出高斯定理，不仅使我们在电磁学中较容易地引进高斯定理，而且使学生对高斯定理有比较准确地、深刻地理解，更重要的是对学生综合运用所学知识的能力的一个训练，收到较好的效果。

1 同济大学应用数学系.高等数学（第五版）［M］.北京：高等教育出版社，2005

2 施传柱.关于高斯定律应用的探讨［J］.曲靖师专学报，1996（6）：20～21

3 马文蔚.物理学中册（第四版）［M］.北京：高等教育出版社，2008