矩形轴向有界磁场均匀变化时激发的涡旋电场的电场线方程
姜付锦 郎 军
(1. 湖北省武汉市黄陂区第一中学,湖北 武汉 430300; 2. 重庆市第十一中学校,重庆 400061)
1 提出问题
矩形轴向有界磁场随时间变化时,在周围产生的感生电场是怎样分布的呢?目前普遍认为,感生电场线是椭圆或圆,[1]可是,这个结论是严格的还是近似的,精度有多高?为此,笔者计算了矩形有界磁场的感生电场,写出了感生电场线的方程,最后运用Maple数值模拟出了涡旋电场线的分布,发现了其感生电场线不是标准的椭圆或圆.
2 研究方法

图1
2.1 计算涡旋电场强度的方法[1-4]
(1)
(1)式是对边界内、外的区域都统一成立的式子.
2.2 涡旋电场线方程的推导
(2)
(2)式是对边界内、外区域都适用的电场线方程.这也表明,边界内、外的电场线方程在形式上是可以统一的.原则上,电场线方程可由(2)式确定,但这个积分式太复杂,连Maple软件都无法计算.
对整个涡旋电场,一般不能引入标量势,但对于对边界外的区域,由于涡旋电场强度的旋度处处为0(×E≡0),类似磁场在无电流分布的区域可以引入磁标势一样,我们也可以引入标量势φ,可得E=-φ,即根据解析函数的实部函数和虚部函数对应曲线簇在空间处处正交的性质,若将φ作为解析函数的实部,通过构造一个解析函数而求虚部E,即得电场线方程.
设电场线方程为E(x,y)=C,由柯西——黎曼方程有
所以
(3)
E(x,y)=C可以表示边界外部区域的电场线的方程.
对于磁场边界以内的区域,虽然涡旋电场强度的旋度不为0,不能引入标量势描述,但正如前述分析,由于边界内、外的电场线方程是可以统一的,且用柯西——黎曼方程得到的电场线方程是未经简化的最一般的形式,因此E(x,y)=C也实际上可以表示边界内部的电场线方程.
设磁场的边界为-a≤x≤a,-b≤y≤b,则(1)式的积分变为
Ex(x,y)=
Ey(x,y)=
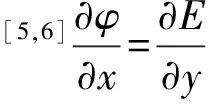
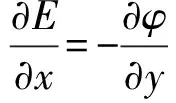
2.3 电场线方程的解析式
由于表达式过于复杂,为了研究问题的方便不妨设a=2,b=1,用Maple软件计算得两个方向上的分电场强度为
其中A1=ln(x2+y2+4x+2y+5),A2=ln(x2+y2+4x-2y+5),A3=ln(x2+y2-4x+2y+5),A4=ln(x2+y2-4x-2y+5).

得电场线方程为
上式中C为某一待定的常数.由此可见电场线方程异常复杂,不可能转化为标准的圆和椭圆.根据得到的电场线方程,借助Maple计算,还可以发现在边界外的区域有
即满足拉普拉斯方程,通过对(1)式的分析表明,电场线方程式是对边界内、外的区域都统一成立的.
3 数值模拟
根据电场线方程,用Maple软件绘出了边界内、外的涡旋电场线分布(图2-图5),与文献[7]得到的结果一致.需要说明的是,从电场线方程的表达式可以看出,4条边界是奇异点区域,导致Maple只能分别绘制边界内、外的电场线.
3.1 正方形边界(a=b=1,k=2π)
图2及图3外边框中心处粗线的边框表示正方形边界,图2是正方形边界外部的感生电场线分布图,图3是正方形边界内部的感生电场线分布图,可以看出它们像圆,但是由解析式可知它们都不是圆.

图2

图3
3.2 长方形边界(a=2,b=1,k=2π)
图中虚线的边框表示长方形边界,图4是长方形边界外部的感生电场线分布图,图5是长方形内部的感生电场线分布图,可以看出它们很像椭圆,但是由解析式可知它们都不是.

图4 长方形边界内部的感生电场分布

图5 长方形边界外部的感生电场分布
4 小结
通过以上的研究可以发现,边界内部与外部的电场线方程是可以统一的,对边界外部由柯西——黎曼方程得出的电场线方程的解析式对边界内部也适用.当磁场边界为矩形时,涡旋电场线方程不是标准椭圆.若边界是其它形状的,运用本文中方法也可以研究,限于文章的篇幅本文不再赘述.

